FFT が一般に知られるようになったのは,1965 年の J.W.Cooley と J.W.Tukey による短い論文からです [参考文献].それ以前にも, 一部の人たちは FFT の算法について気づいていたようですが,広く 知られることはありませんでした.FFT があまり知られていなかったころは, 長さ N の離散 Fourier 変換を計算するためには N^2 回の計算が必要であると 信じられていました.しかし,FFT を用いると N*log(N) に比例する計算で 済みます.この違いは具体的には,一秒間に 10^9 回の演算ができる コンピュータで N=2^30 の離散 Fourier 変換を実行した場合に,30 年と 3 分の違いになります.この FFT の基本原理はコロンブスの卵的な発想で, 一言でいえば大きな問題を計算が楽な小さな問題に分解するというものです. この分解の方法はいくつかあり,ここでは Cooley と Tukey の示した 分解による FFT を紹介します.
まず,長さ N の DFT
N-1 jk -2πi / N
A = Σ a W , W = e
k j=0 j N N
を素直に計算する場合を考えます.この場合 A_0 から A_N-1 までの各項の 計算に N 回の乗算が必要なため,全体で N^2 回の乗算が必要になります. しかし,少し考えてみてください.もし,N が 2 で割り切れるならば, 添字 k を偶数と奇数とに分けることで,長さ N の DFT は,次の二つの, 長さ N/2 の DFT
N/2-1 jk
A = Σ (a + a ) W
2k j=0 j N/2+j N/2
N/2-1 j jk
A = Σ ((a − a ) W ) W
2k+1 j=0 j N/2+j N N/2
に分解できることがわかると思います.長さ N/2 の DFT は,素直に 計算すると N^2/4 回の乗算で実行できるので,この分解により,計算量は 約半分に減ります.さらに,この分解を 2 回, 3 回,... と繰り返せば, 計算量は約 1/4, 1/8,... と激減します.これが Cooley-Tukey 型の FFT (正確には,基数 2, 周波数間引き Cooley-Tukey 型 FFT)の基本的な 考え方です.これを小細工をせずに直接 C のコードに直すと次のように なります.
| リスト1.2.1-1. 再帰呼び出しによる FFT |
|---|
/*
F[k]=Σ_j=0^n-1 a[j]*exp(±2*pi*i*j*k/n),0<=k<n を計算する.
n はデータ数で 2 の整数乗, theta は ±2*PI/n,
ar[0...n-1], ai[0...n-1], はデータの実部, 虚部,
tmpr[0...n-1], tmpi[0...n-1] は作業領域.
*/
#include <math.h>
void fft(int n, double theta, double ar[], double ai[],
double tmpr[], double tmpi[])
{
int nh, j;
double xr, xi, wr, wi;
if (n <= 1) return;
nh = n / 2;
for (j = 0; j < nh; j++) {
tmpr[j] = ar[j] + ar[nh + j];
tmpi[j] = ai[j] + ai[nh + j];
xr = ar[j] - ar[nh + j];
xi = ai[j] - ai[nh + j];
wr = cos(theta * j);
wi = sin(theta * j);
tmpr[nh + j] = xr * wr - xi * wi;
tmpi[nh + j] = xi * wr + xr * wi;
}
fft(nh, 2 * theta, tmpr, tmpi, ar, ai);
fft(nh, 2 * theta, &tmpr[nh], &tmpi[nh], ar, ai);
for (j = 0; j < nh; j++) {
ar[2 * j] = tmpr[j];
ai[2 * j] = tmpi[j];
ar[2 * j + 1] = tmpr[nh + j];
ai[2 * j + 1] = tmpi[nh + j];
}
}
|
このルーチンは,log(N) 段の再帰呼び出しをします.その各々の段で N/2 回の複素数乗算と N 回の複素数加算を行います.したがって, 複素数乗算回数は (N/2)*log(N) に減少し,浮動小数点演算の量は N*log(N) のオーダーになることがわかります.これは,Cooley-Tukey 型 FFT の典型的な演算量で,どんなに高速な Cooley-Tukey 型 FFT ルーチンも このオーダーになります.様々な Cooley-Tukey 型 FFT の演算量の削減は, このオーダーの比例定数と,N*log(N) より低い次数の項を小さくする 技法によるものです.
次に,このルーチンの変形について考えます.他の多くの Cooley-Tukey 型 FFT ルーチンは,このルーチンの機械的な変形で導くことができます.まず, 再帰呼び出しは容易にループに展開できます.さらに,出力データの順番を 気にしなければ,このルーチンの作業領域と最後の並べ替えのループは省略 できます.そこで,データの並べ替えを省略したときの出力の順番について 考えます.まず,最初の段だけを考えると,ルーチン内のデータ a_j, a_n/2+j には正しい順の結果 A_2j, A_2j+1 が上書きされることに なります.添字に注目すると,a の添字 j, n/2+j は A の添字 2j, 2j+1 を 1 ビット右に巡回したもので,1 の位のビットが n/2 の位のビットに移動し, その他のビットがシフトしていることがわかります.したがって,すべての 段の再帰呼び出しを考慮すると,出力データの添字は正しいデータの添字を ビット反転した順になります.データの順をもとに戻すためには, 添字のビット反転の並べ替えをするルーチン が必要になります.これらの変更を行うと,次のようになります.
| リスト1.2.1-2. 基数 2 の周波数間引き FFT |
|---|
#include <math.h>
void fft(int n, double theta, double ar[], double ai[])
{
int m, mh, i, j, k;
double wr, wi, xr, xi;
for (m = n; (mh = m >> 1) >= 1; m = mh) {
for (i = 0; i < mh; i++) {
wr = cos(theta * i);
wi = sin(theta * i);
for (j = i; j < n; j += m) {
k = j + mh;
xr = ar[j] - ar[k];
xi = ai[j] - ai[k];
ar[j] += ar[k];
ai[j] += ai[k];
ar[k] = wr * xr - wi * xi;
ai[k] = wr * xi + wi * xr;
}
}
theta *= 2;
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = ar[j];
xi = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = xr;
ai[i] = xi;
}
}
}
|
このルーチンは in-place 演算と呼ばれ,log(N) 回ある各々の段でデータは 上書きされています.これは,変形の一つの例で,非 in-place 演算への変形も 可能です.しかし,これらの変形は漸化式を用いて行う方が簡単です.まず, このルーチンの n = log(N) 段あるバタフライ演算の m 段目のデータを
X (j, k) = a[j + bitreversal(k)]
m
m-1 n-m
0 <= k < 2 , 0 <= j < 2
と置きます.bitreversal(k) は k のビット反転とします.このとき, このルーチンは次の漸化式
n-m
X (j, k) = X (j, k) + X (j + 2 , k)
m m-1 m-1
m-1 n-m m-1
X (j, k + 2 ) = (X (j, k) − X (j + 2 , k) ) W (j 2 )
m m-1 m-1 N
に置き換えられ,この漸化式を m = 1, 2, 3,...n (n=log(N)) に対して 計算していることになります.ここで,X(j,k) は 2^(n-m) x 2^m の 行列です.この漸化式をそのままプログラムにすれば,ビット反転の操作は なくなります.しかし,データの上書きは困難になり,X(j,k) を格納する 作業用の配列が必要になります.一般に,データの上書きを行うためには, j または k のどちらかに対してビット反転をおこない,漸化式でのデータの 参照及び書き込みが常に同じ位置になるようにします.
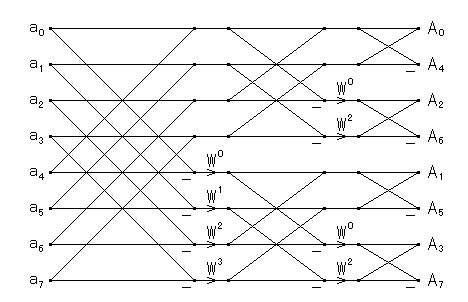
次に,上のルーチンについて少し調べます.まず,長さが 8 のときの データフローは次のようになります.
 |
| 図1.2.1-1. 基数 2 の周波数間引き FFT のフローグラフ |
|---|
このフローグラフは,二つのデータを足し引きし W を掛けるという基本演算 からできています.この演算は蝶の形に似ていることからバタフライ演算と 呼ばれています.また,バタフライ演算に含まれる W を回転因子と いいます.
このルーチンは 1 バタフライルーチンと呼ばれ,多くの不要な演算が 含まれます.W の値が 1, i のときの乗算は除去することができ,さらに W の値が exp(πi/4), exp(3πi/4) のときの乗算(実数乗算)は半分に できます.一般に,Cooley-Tukey 型 FFT の不要な乗算を完全に取り除く ためには,回転因子の値に応じて五つの場合に分ける必要があります. このとき,5 つのバタフライルーチンが必要になります.しかし,実際の ルーチンでは,計算量とプログラムの複雑さとのトレードオフから, W = 1, i のときの不要な乗算を取り除く 3 バタフライルーチン,または W = 1 のときの不要な乗算を取り除く 2 バタフライルーチンとします.
次に,このルーチン (基数 2 の FFT)の演算量について考えます. N 点の複素 DFT の計算に必要な実数乗算回数 μ と実数加算回数 α は 次のようになります.
μ = 2N log N - 7N + 12
α = 3N log N - 3N + 4
ただし,これは 5 バタフライルーチンを用いて不要な演算を取り除き, 複素乗算を 4 回の実数乗算と 2 回の実数加算で計算したときの値です.
次に,このルーチンのループの変形について考えます.まず, 三重ループの二番目と三番目は入れ換えができ,添字を連続にできます. 特に,この場合は計算量を少なくするために,三角関数をテーブルにして 参照することが必要になります.また,このようなループの入れ替えを 行わずにデータ参照を連続化することもできます.これは,バタフライ ルーチン内の添字を単にビット反転することで可能になります.この添字の ビット反転を実行すると,最後にあったビット反転並べ替えがキャンセルされ, ルーチンの最初に来ます.また,三角関数の引数の添字はビット反転されます. この変形は,上の漸化式で j についてビット反転を行ったものに相当します. このときのルーチンは次のようになります.
| リスト1.2.1-3. 基数 2 の周波数間引き FFT (修正版) |
|---|
#include <math.h>
void fft(int n, double theta, double ar[], double ai[])
{
int m, mh, i, j, k, irev;
double wr, wi, xr, xi;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = ar[j];
xi = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = xr;
ai[i] = xi;
}
}
for (mh = 1; (m = mh << 1) <= n; mh = m) {
irev = 0;
for (i = 0; i < n; i += m) {
wr = cos(theta * irev);
wi = sin(theta * irev);
for (k = n >> 2; k > (irev ^= k); k >>= 1);
for (j = i; j < mh + i; j++) {
k = j + mh;
xr = ar[j] - ar[k];
xi = ai[j] - ai[k];
ar[j] += ar[k];
ai[j] += ai[k];
ar[k] = wr * xr - wi * xi;
ai[k] = wr * xi + wi * xr;
}
}
}
}
|
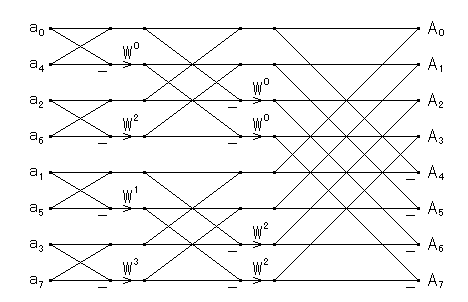 |
| 図1.2.1-2. 基数 2 の周波数間引き FFT (修正版)のフローグラフ |
|---|
このルーチンは,多くの状況で高速になるのでよく利用されます.さらに, 実数データの DFT や離散コサイン変換などへの応用で,対称性を利用して 不要な計算の削除を行う場合は,この変形はとくに重要になります.
実際のルーチンでは,後に示すいろいろな効率的なアルゴリズムを 用い,FFT の無数にある細かい変形を行います.しかし,これらの FFT の アルゴリズムの基本的な考えはほぼ同じで,大きなサイズの問題を,より 計算が楽な小さなサイズに分解するという考え方に基づいています.