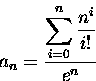
Acta Math. Acad. Paed. Nyíregyháziensis
15 (1999), 35-40
www.bgytf.hu/~amapn
The object of this article is to examine the sequence
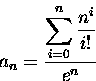
well known from probability theory. We prove that the sequence is bounded,
strictly monotonously decreasing, and ![]() The last two statements are proved by analytical
means. Finally, a modification and a generalization of (an) will
be mentioned, and the sketch of a second analytical proof for the original
limit will be given.
The last two statements are proved by analytical
means. Finally, a modification and a generalization of (an) will
be mentioned, and the sketch of a second analytical proof for the original
limit will be given.
Mathematics Subject Classification. 26A12, 26A42, 40A05.
Key words and phrases. Limit, probability, analytical means.