Journal of Integer Sequences, Vol. 2 (1999), Article 99.1.5

Balls on the Lawn


Colin L. Mallows
AT&T Research Labs
180 Park Avenue
Florham Park, NJ 07932
Email address: clm@research.att.com

Lou Shapiro
Math Dept.
Howard University
Washington, DC 20059
Email address: lws@scs.howard.edu

Abstract: In the "tennis ball" problem we are given successive pairs of balls numbered (1,2), (3,4),... At each stage we throw one ball out of the window. After n stages some set of n balls is on the lawn. We find a generating function and a closed formula for the sequence     3,23,131,664,3166,14545,65187,287060,1247690,...,     the n-th term of which gives the sum over all possible arrangements of the total of the numbers on the balls on the lawn. The problem has connections with "bicolored Motzkin paths" and the ballot problem.



1. Introduction.

The tennis ball problem goes as follows. At the first turn you are given balls numbered 1 and 2. You throw one of them out the window onto the lawn. At the second turn balls numbered 3 and 4 are brought in and now you throw out on the lawn any of the three balls in the room with you. Then balls 5 and 6 are brought in and you throw out one of the four available balls. The game continues for n turns. The first question is how many different arrangements on the lawn are possible. It is easy to see that there are 2, 5 and 14 possibilities after 1, 2 and 3 turns. This suggests the Catalan numbers which turns out to be the case. A more delicate question is "what is the total sum of the balls on the lawn over all these possibilities"? Here the first few terms are 3, 23, 131 and 664. As an example consider the five possibilities after two turns. They are $\left\{ 1,2\right\}$, $\left\{ 1,3\right\}$, $\left\{ 1,4\right\}$,$\left\{ 2,3\right\}$ or $\left\{ 2,4\right\}$.The total sum is $\left( 1+2\right) +\left( 1+3\right) +\left( 1+4\right) +\left( 2+3\right) +\left( 2+4\right) =23$.

We will find both a generating function and a closed formula for this sequence. First we return to the first question and transform it to a question about paths.

Let $b\left( n,k\right)$ be the number of possible paths that end at $\left( n,k\right)$. Here is a table of small values

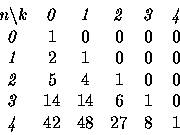
\begin{displaymath} \begin{array} {cccccc} n\backslash k & \mathit{0} & \mathit{... ... 14 & 6 & 1 & 0 \ \mathit{4} & 42 & 48 & 27 & 8 & 1\end{array}\end{displaymath}

We can make three observations. One is that with the four kinds of steps we get the recursion

\begin{displaymath} b\left( n+1,k\right) =b\left( n,k-1\right) +2b\left( n,k\right) +b\left( n,k+1\right) .\end{displaymath}

This holds for $k,n\geq 0$ if we specify that $b\left( 0,0\right) =1$ and $b\left( n,-1\right) =0$. Both conditions make sense in terms of these paths.

Secondly we have

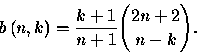
\begin{displaymath} b\left( n,k\right) =\frac{k+1}{n+1}{{2n+2}\choose{n-k}}.\end{displaymath}

Given the recursion, this is easily established by induction.

Thirdly $b\left( n,0\right) =\frac{1}{n+2}{{2\left( n+1\right)}\choose{n+1}},$the $\left( n+1\right) ^{st}$ Catalan number (see [6] and [7] for different proofs).

Now we return to the balls on the lawn after $n\,$turns. Let us look at a typical example after 6 turns.

\begin{displaymath} \begin{array} {c@{~}c@{~}c@{~}c@{~}c@{~}c@{~}c@{~}c@{~}c@{~}... ...9,10 & / & 11, 12' \ ^l && ^U && ^L && ^L &&^D &&^l\end{array}\end{displaymath}

The balls on the lawn are denoted by "$\prime$". As we read from left to right one pair at a time, we must always have as many or more pairs with both balls selected as with no balls selected with equality at the end. If both balls are selected mark the pair with a U, if neither is selected mark with a D, if the odd member is the one selected use an L, if the even number was selected then use an l. This sets up an obvious correspondence with the bicolored Motzkin paths ending at height zero and this shows that the number of possibilities after n turns is the Catalan number Cn+1.

We now want to shift back to subdiagonal paths from $\left( 0,0\right) $ to $\left( n+1,n+1\right) $ using unit east and north steps. If we number the steps along each such path starting at the origin using the numbers to 2n+1, then the numbers of the horizontal steps correspond to the numbers of the balls on the lawn except that we ignore the initial horizontal step numbered 0. All subdiagonal paths must go from $\left( 0,0\right) $ to $\left( 1,0\right) $ at the first step so let us look on $\left( 1,0\right) $as our starting point and $\left( n+1,n\right) $ as the terminal point. We then look at steps in pairs to set up a correspondence with bicolored Motzkin paths

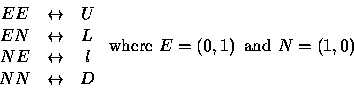
\begin{displaymath} \begin{array} {ccc} EE & \leftrightarrow & U \ EN & \leftri... ...box{ where }E=\left( 0,1\right) \mbox{ and }N=\left( 1,0\right)\end{displaymath}

To evaluate the sum over all possible sets of balls on the lawn takes a bit more doing and its worthwhile to separate out some definitions and lemmas first.


2. Definitions and notation.

The nth Catalan number is $C_{n}= \frac{1}{n+1}{{2n}\choose{n}}$.The generating function for the sequence of Catalan numbers is $C=C\left( z\right) =\sum_{n=0}^{\infty}C_{n}z^{n}=\frac{1-Q}{2z}$where Q= $\sqrt{1-4z}$.Similarly $B=B\left( z\right) =\sum_{n=0}^{\infty }{{2n}\choose{n}}z^{n}=\frac{1}{Q}$ is the generating function for the sequence of central binomial coefficients.

The following lemmas can be proved combinatorially but instead we refer to Concrete Mathematics [4], page 203, formulas $\left( 5.80\right) $ and $\left( 5.82\right) $ for the first two lemmas and leave the others as exercises.

Lemma 1

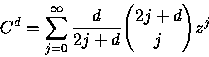
\begin{displaymath} C^{d}=\sum_{j=0}^{\infty }\frac{d}{2j+d}{{2j+d}\choose{j}}z^{j}\end{displaymath}

Lemma 2

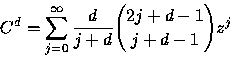
\begin{displaymath} C^{d}=\sum_{j=0}^{\infty }\frac{d}{j+d}{{2j+d-1}\choose{j+d-1}}z^{j}\end{displaymath}

Lemma 3

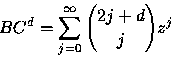
\begin{displaymath} BC^{d}=\sum_{j=0}^{\infty }{{2j+d}\choose{j}}z^{j}\end{displaymath}

Lemma 4

\begin{displaymath} B=\frac{C}{1-zC^{2}}\mbox{ or alternatively }\frac{1}{1-zC^{2}}=\frac{B}{C}\end{displaymath}

Lemma 5

\begin{displaymath} 2B=C\left( 1+B\right)\end{displaymath}

Lemma 6

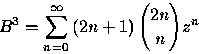
\begin{displaymath} B^{3}=\sum_{n=0}^{\infty }\left( 2n+1\right) {{2n}\choose{n}}z^{n}\end{displaymath}

Lemma 7

The number of subdiagonal paths from $\left( 0,0\right) \,$to $\left( i,j\right) $ will be denoted $N\left( i,j\right) $ and

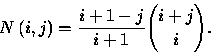
\begin{displaymath} N\left( i,j\right) =\frac{i+1-j}{i+1}{{i+j}\choose{i}}.\end{displaymath}

This is the cornerstone result about ballot numbers and a reference which summarizes this and much of the related literature is[2].

We now want to embark on the main computation. Note first that

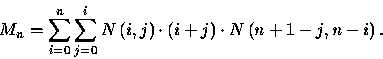
\begin{displaymath} M_{n}=\sum_{i=0}^{n}\sum_{j=0}^{i}N\left( i,j\right) \cdot \left( i+j\right) \cdot N\left( n+1-j,n-i\right) .\end{displaymath}

Before launching into the evaluation lets look at each term. There are $N\left( i,j\right) $ paths from $\left( 0,0\right) $to $\left( i,j\right) $and $N\left( n+1-j,n-i\right)$ paths from $\left( i+1,j\right)$ to $\left( n+1,n+1\right) $.What does it mean for a path to have arrived at $\left( i,j\right) $? Of the balls $\left\{ 1,2,\ldots ,i+j-1\right\}$, i-1 of them are on the lawn and j of them are to stay in the room. The horizontal step $\left( i,j\right) \rightarrow \left( i+1,j\right) $ indicates that ball number i+j is to be on the lawn and hence the term $\left( i+j\right)$.By Lemma 7 we then get

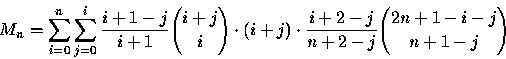
\begin{displaymath} M_{n}=\sum_{i=0}^{n}\sum_{j=0}^{i}\frac{i+1-j}{i+1}{{i+j}\ch... ... i+j\right) \cdot \frac{i+2-j}{n+2-j}{{2n+1-i-j}\choose{n+1-j}}\end{displaymath}

We want to find a closed form for the generating function

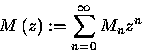
\begin{displaymath} M\left( z\right) :=\sum_{n=0}^{\infty }M_{n}z^{n}\end{displaymath}

If we set n=m+i and then i=j+d we obtain

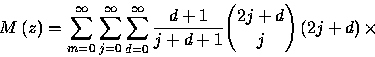
\begin{displaymath} M\left( z\right) =\sum_{m=0}^{\infty }\sum_{j=0}^{\infty }\... ...y }\frac{d+1}{j+d+1}{{2j+d}\choose{j}}\left( 2j+d\right) \times\end{displaymath}

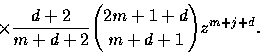
\begin{displaymath} \times \frac{d+2}{m+d+2}{{2m+1+d}\choose{m+d+1}}z^{m+j+d}.\end{displaymath}

We sum on m first; then invoke Lemma 2.

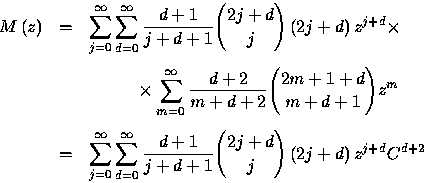
\begin{displaymath} \begin{array} {rll} M\left( z\right) & = &\displaystyle\sum_... ...{{2j+d}\choose{j}} \left( 2j+d\right) z^{j+d}C^{d+2}\end{array}\end{displaymath}

By rewriting 2j+d=2j+d+1-1 we get $M\left( z\right) =P-R$where

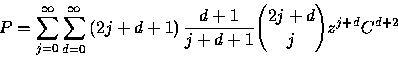
\begin{displaymath} P=\sum_{j=0}^{\infty }\sum_{d=0}^{\infty }\left( 2j+d+1\right) \frac{d+1}{j+d+1}{{2j+d}\choose{j}}z^{j+d}C^{d+2}\end{displaymath}

and

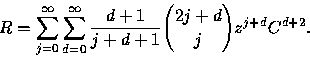
\begin{displaymath} R =\sum_{j=0}^{\infty }\sum_{d=0}^{\infty }\frac{d+1}{j+d+1}{{2j+d}\choose{j}}z^{j+d}C^{d+2}.\end{displaymath}

However, with the aid of Lemmas 3 and 4, we obtain

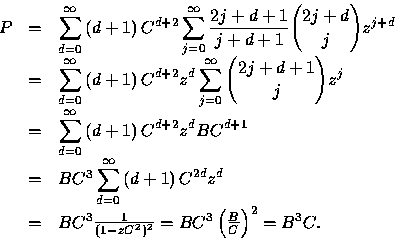
\begin{displaymath} \begin{array} {rcl} P &=&\displaystyle\sum_{d=0}^{\infty }\l... ...})^2} = BC^{3}\left( \frac{B}{C}\right) ^{2}=B^{3}C.\end{array}\end{displaymath}

For the second term we have, via Lemmas 2 and 4,

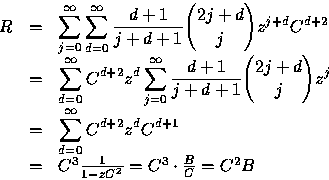
\begin{displaymath} \begin{array} {rcl} R &=& \displaystyle\sum_{j=0}^{\infty }\... ...}\frac{1}{1-zC^{2}} = C^{3} \cdot \frac{B}{C}=C^{2}B\end{array}\end{displaymath}

Thus $M\left( z\right) =B^{3}C-C^{2}B.$

3. Remarks.

1.

\begin{displaymath} M\left( z\right) =\frac{C^{3}B^{3}}{z}\left( 1+\frac{2}{B}\right) =\frac{C^{3}}{z\left( 1-4z\right) }\left( B+2\right) .\end{displaymath}

2.

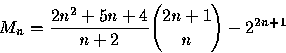
\begin{displaymath} M_{n}=\frac{2n^{2}+5n+4}{n+2}{{2n+1}\choose{n}}-2^{2n+1}\end{displaymath}

3.
There is also a connection with hypergeometric functions.

\begin{displaymath} C^{d}=\,_{1}F_{2}\left( \frac{d}{2},\frac{d+1}{2};d+1;4z\right)\end{displaymath}

and

\begin{displaymath} BC^{d}= \,_{1}F_{2}\left( \frac{d+1}{2},\frac{d+2}{2};d+1;4z\right)\end{displaymath}

The first and third of these remarks can be shown by routine algebraic manipulations and the second follows from the first as follows:

\begin{displaymath} \begin{array} {rcl} zC^{3}B^{3}\left( 1+\displaystyle\frac{2... ...B^{3}+\frac{1}{z^{2}}B^{2}-5\frac{B^{2}}{z}\right] .\end{array}\end{displaymath}

since Q2=1-4z. But $B^{2}=\sum_{n=0}^{\infty }4^{n}z^{n}$ while $B^{3}=\sum_{n=0}^{\infty }\left( 2n+1\right) {{2n}\choose{n}}$.Thus extracting nth terms yields

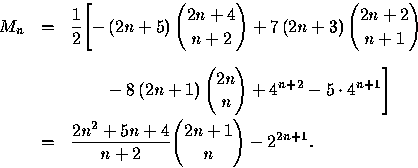
\begin{displaymath} \begin{array} {rcl} M_{n}& = &\displaystyle\frac{1}{2}\Biggl... ...+5n+4}{n+2}{\displaystyle{2n+1}\choose{n}}-2^{2n+1}.\end{array}\end{displaymath}

Two other remarks can be made here. First, an asymptotic result,

\begin{displaymath} M_{n}\sim 4^{n}\left( 4\sqrt{\frac{n}{\pi }}-2\right) .\end{displaymath}

Second, the expected value of the balls on the lawn is $\frac{n\left( 4n+5\right) }{6}$ if we assume each available ball is equally likely to be picked at each turn.

Problem 19(s) of reference [7] is succinct but less colorful. It asks one to show that the Catalan numbers count sequences of positive integers such that $a_{1}a_{2}\cdots a_{n}$ and $a_{i}\leq 2i$.The references there point out a connection with an indexing of the weights of the $\left( n-1\right) st$ fundamental representation of the symplectic group $Sp\left( 2n-2,\Bbb{C}\right)$.

The problem was brought to our attention by Ralph Grimaldi, see [6], who refers to the logic text [8] where it is pointed out that after an infinite number of turns the balls remaining in the room can be either the empty set, a finite set of arbitrary size or even an infinite set such as all the even numbered balls.

References

1
Barcucci E., R. Pinzani, & R. Sprugnoli, The Motzkin family, PU.M.A. Ser. A, 2 (1991) 249-279.

2
Barton, D. E. & C. L. Mallows, Some aspects of the random sequence, Ann. Math. Stat., 36 (1965) 236-260.

3
Donaghey R. & L. W. Shapiro, The Motzkin numbers, J. Combinatorial Theory Ser. A, 23 (1977) 291-301.

4
Graham R., D. E. Knuth & O. Patashnik, Concrete Mathematics, Addison-Wesley, 1990.

5
Getu S. & L. Shapiro, Catalan and Motzkin probabilities, (to appear), Congressus Numerantium.

6
Grimaldi R. & J. Moser, The Catalan numbers and the tennis ball problem, Congressus Numerantium, 125 (1997) 65-71.

7
Stanley, R. P., Enumerative Combinatorics, volume 2, to appear, Cambridge University Press.

8
Tymoczko T.& J. Henle, Sweet Reason: A Field Guide to Modern Logic, Freeman, 1995, p. 304.

(Concerned with sequence A031970 .)

Received July 17 1998; revised version received January 13 1999. Published in Journal of Integer Sequences March 15 1999.

Return to Journal of Integer Sequences home page