 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.8.4 |
 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.8.4 |
Abstract:
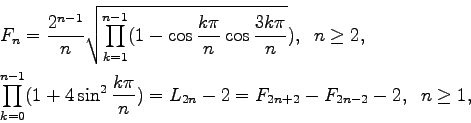
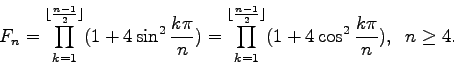
(Concerned with sequences A000032 A000045.)
Received November 16 2009; revised version received November 26 2009. Published in Journal of Integer Sequences, November 29 2009.