 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.7.4 |
 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.7.4 |
Abstract:
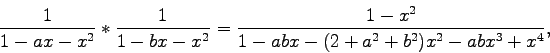
(Concerned with sequences A000045 A007598 A011973 A093614 A114525.)
Received March 3 2009; revised version received October 20 2009. Published in Journal of Integer Sequences, October 21 2009.