Jean C.-C. Yeh
Department of Mathematics
Texas A & M University
College Station, TX 77843-3368
USA
In this paper, we develop a systematic tool to calculate the
congruences of some combinatorial numbers involving
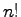
. Using this
tool, we re-prove Kummer's and Lucas' theorems in a unique concept, and
classify the congruences of the Catalan numbers
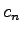
(mod
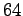
). To
achieve the second goal,
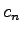
(mod
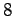
) and
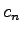
(mod
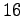
) are also
classified. Through the approach of these three congruence problems, we
develop several general properties. For instance, a general formula
with powers of
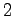
and
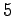
can evaluate
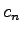
(mod
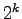
) for any
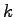
.
An equivalence
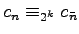
is derived, where
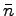
is the number obtained by partially truncating some runs of
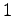
and runs of
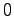
in the binary string
![$[n]_2$](abs/img14.gif)
. By this equivalence
relation, we show that not every number in
![$[0,2^k-1]$](abs/img15.gif)
turns out to be a
residue of
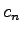
(mod
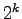
) for
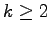
.

