The Generalized Stirling and Bell Numbers Revisited
Toufik Mansour
Department of Mathematics
University of Haifa
31905 Haifa
Israel
Matthias Schork
Camillo-Sitte-Weg 25
60488 Frankfurt
Germany
Mark Shattuck
Department of Mathematics
University of Tennessee
Knoxville, TN 37996
USA
Abstract:
The generalized Stirling numbers
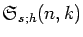 introduced
recently by the authors are shown to be a special case of the three
parameter family of generalized Stirling numbers
introduced
recently by the authors are shown to be a special case of the three
parameter family of generalized Stirling numbers
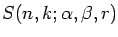 considered by Hsu and Shiue. From this
relation, several properties of
considered by Hsu and Shiue. From this
relation, several properties of
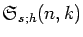 and the
associated Bell numbers
and the
associated Bell numbers
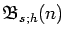 and Bell polynomials
and Bell polynomials
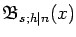 are derived. The particular case s=2 and
h=-1 corresponding to the meromorphic Weyl algebra is treated
explicitly and its connection to Bessel numbers and Bessel polynomials
is shown. The dual case s=-1 and h=1 is connected to Hermite
polynomials. For the general case, a close connection to the Touchard
polynomials of higher order recently introduced by Dattoli et al. is
established, and Touchard polynomials of negative order are introduced
and studied. Finally, a q-analogue
are derived. The particular case s=2 and
h=-1 corresponding to the meromorphic Weyl algebra is treated
explicitly and its connection to Bessel numbers and Bessel polynomials
is shown. The dual case s=-1 and h=1 is connected to Hermite
polynomials. For the general case, a close connection to the Touchard
polynomials of higher order recently introduced by Dattoli et al. is
established, and Touchard polynomials of negative order are introduced
and studied. Finally, a q-analogue
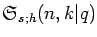 is
introduced and first properties are established, e.g., the
recursion relation and an explicit expression. It is shown that the
q-deformed numbers
is
introduced and first properties are established, e.g., the
recursion relation and an explicit expression. It is shown that the
q-deformed numbers
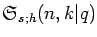 are special cases of
the type-II p,q-analogue of generalized Stirling numbers
introduced
by Remmel and Wachs, providing the analogue to the undeformed case
(q=1). Furthermore, several special cases are discussed explicitly,
in particular, the case s=2 and h=-1 corresponding to the
q-meromorphic Weyl algebra considered by Diaz and Pariguan.
are special cases of
the type-II p,q-analogue of generalized Stirling numbers
introduced
by Remmel and Wachs, providing the analogue to the undeformed case
(q=1). Furthermore, several special cases are discussed explicitly,
in particular, the case s=2 and h=-1 corresponding to the
q-meromorphic Weyl algebra considered by Diaz and Pariguan.
Full version: pdf,
dvi,
ps,
latex
(Concerned with sequences
A000110
A000369
A001497
A008275
A008277
A008297
A035342
A069223
A078739
A078740
A144299.)
Received July 17 2012;
revised version received October 1 2012.
Published in Journal of Integer Sequences,
October 2 2012.
Return to
Journal of Integer Sequences home page

