 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.7.6 |
 |
Journal of Integer Sequences, Vol. 16 (2013), Article 13.7.6 |
António Guedes de Oliveira
CMUP and Department of Mathematics
Faculty of Sciences
University of Porto
Portugal
Abstract:
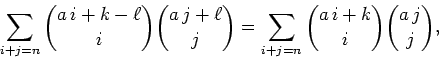
(Concerned with sequences
A000302
A000984
A006256
A078995.)
Received February 8 2013; revised versions received March 8 2013; July 26 2013; August 21 2013. Published in Journal of Integer Sequences, August 22 2013.