 |
Journal of Integer Sequences, Vol. 3 (2000), Article 00.1.6 |
 |
Journal of Integer Sequences, Vol. 3 (2000), Article 00.1.6 |
Abstract: In 1991 the author investigated a class of lattice paths that are connected with the Catalan numbers in an unusual way. Soon after, combinatorial proofs for these results were found independently by Krattenthaler and Sagan, and are included here as an Addendum. There is also an extensive annotated bibliography.
Editorial Note: Although the Encyclopedia of Integer Sequences contains numerous references to this paper, originally written in 1991, it has never before been published. This updated version is included in the Journal of Integer Sequences at the invitation of the editors.
Bill Sands [9, where the problem is stated without the result (1)] noticed that the number of different walks of n steps between lattice points, each in a direction N, S, E or W, starting from the origin and remaining in the upper half-plane, is
![]()
and asked for a short proof. What is wanted is a simple ``choice'' argument. This is sequence A001700 in [10]: my first attempt was by induction from the formula
![]()
since a walk of length n is one more step in one of the four directions N, S, E or W, than a walk of length n-1, except that a southerly step is not allowed if the walk of length n-1 terminated on the x-axis, and it is well known that the number of such walks is the n-th Catalan number.
But it is not well known! It doesn't occur among the 31 manifestations listed by Kuchinski [6], nor can we immediately see any simple correspondence between the walks and any of the manifestations. However, first let us assume that it is true, and that (1) holds with n-1 in place of n. Then
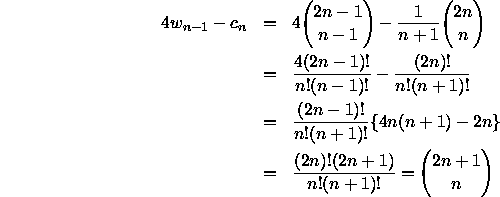
What is well known is that the number of walks of 2n steps, each
N or E, from (0,0) to (n,n), which don't cross the diagonal y = x,
or the number of walks of 2n+2 steps from (0,0) to (n+1,n+1) which
stay strictly above the diagonal, is ![]() , the n-th Catalan number.
This is clearly the same as the number of walks of 2n steps on the
positive x-axis, starting and finishing at the origin.
, the n-th Catalan number.
This is clearly the same as the number of walks of 2n steps on the
positive x-axis, starting and finishing at the origin.
Let us look at this one-dimensional analog of the Sands problem. We can
exhibit the numbers of walks, w(n,x), of n unit steps, starting at
(0,0) and ending at (x,0), ![]() , in a ``Pascal semi-triangle''
(Fig. 1).
, in a ``Pascal semi-triangle''
(Fig. 1).
Columns x = 0 and x = 1 contain the Catalan numbers, sequence
A000108, as already earnested; column x = 3 (sequence
A002057) also occurs in connexion with partitioning a polygon [1].
Columns x = 2, 4, 6, 8, 10, 12 are sequences
A000245,
A000344,
A000588,
A001392,
A000589,
A000590 in [10]: they are Laplace
transform coefficients: more precisely, w(2n,2k) is denoted in
[7] by ![]() , which is defined by:
, which is defined by:
![]()
Presumably there is an analogous formula for w(2n+1,2k+1); compare equation (11) below. Columns x = 5, 7, 9 are sequences A003517, A003518, A003519. The row sums in Fig. 1, shown at the right, are the central binomial coefficients, A001405. (The triangle of numbers in Fig. 1 now forms sequences A008315 and A052173 in [10], where this is referred to as a Catalan triangle. See also sequence A047072.)
The first table in Cayley's paper [1] is for the number of
partitions of an r-gon into k parts by non-intersecting diagonals.
His column k = 1 is our main diagonal, and his column k = 2 is our
third diagonal (starting at (n,x) = (4,0)). More generally, his column
k is our diagonal starting at (2k,0), except that his entries
contain an extra factor (x+k-2)!/(x+1)!(k-2)!, a generalized Catalan
number: in fact, for x = k-2 it is ![]() . Cayley attributes his
results to [4] and [11]: the latter paper gives some
history, mentioning Terquem, Lamé, Rodrigues, Binet and Catalan.
. Cayley attributes his
results to [4] and [11]: the latter paper gives some
history, mentioning Terquem, Lamé, Rodrigues, Binet and Catalan.
We omit zero values of w(n,x) from our table: it's fairly obvious that w(n,x) = 0 if n and x are of opposite parity, or if x > n. It's not too difficult to find formulas for the first few diagonals:
![]()
In fact there is a comparatively simple formula for all the entries in Figure 1:
![]()
where ![]() . Indeed, the formula (4) also works in the
apocryphal cases mentioned above, if we take the reasonable
interpretation that
. Indeed, the formula (4) also works in the
apocryphal cases mentioned above, if we take the reasonable
interpretation that ![]() if r < 0, or if n < r, or if r is
not an integer. We shall do this: note that the usual formulas, such as
if r < 0, or if n < r, or if r is
not an integer. We shall do this: note that the usual formulas, such as
![]()
and (13) still hold in these cases. Formula (4) is easily proved by induction, since
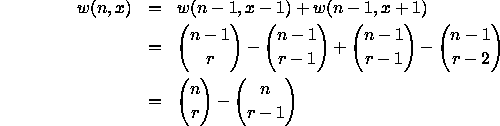
The well known result that we mentioned is the special case
![]()
The total number, w(n), of walks of length n is
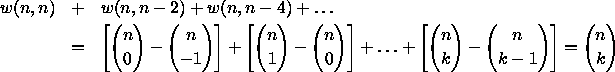
where n-2k = 0 or 1 according as n is even or odd: i.e.
![]()
Here it is clear that the number of walks of even length is just twice the number of walks of (odd) length one less:
![]()
Is there a simple ``choice'' argument for walks of odd length? If you ``know'' the Catalan number result, then we can use a device similar to formula (2):
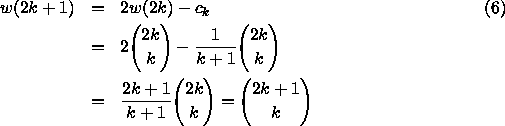
but this has an air of circularity about it, or at best may be using a sledgehammer to crack a nut.
Return to the original problem: we can solve it if we go into more
detail than most people would deem desirable. The numbers, ![]() ,
of walks of n steps from (0,0) to (x,y), which remain in the
half-plane
,
of walks of n steps from (0,0) to (x,y), which remain in the
half-plane ![]() , may be exhibited in a ``Pascal semi-pyramid''
whose layers are shown in Fig. 2.
, may be exhibited in a ``Pascal semi-pyramid''
whose layers are shown in Fig. 2.
Figure 2: Layers of a Pascal semi-pyramid: values of ![]() .
.
If we sum the rows in the layers of Fig. 2 we obtain the numbers,
![]() , of walks of n steps which start at (0,0) and end at distance
y from the x-axis. These are shown in Fig. 3. We shall see that a
special case is, as we have already earnested,
, of walks of n steps which start at (0,0) and end at distance
y from the x-axis. These are shown in Fig. 3. We shall see that a
special case is, as we have already earnested,
![]()
Figure 3: Sums of rows of Fig. 2: values of ![]() .
.
(The triangle of numbers in Fig. 2 now forms sequences A039598 and A050166 in [10].)
In turn, the row sums of Fig. 3 are the total numbers, ![]() , of
Sands-type walks of length n. They are listed in column two of Fig. 3,
and we will confirm another of our earlier statements:
, of
Sands-type walks of length n. They are listed in column two of Fig. 3,
and we will confirm another of our earlier statements:
![]()
At risk of losing some interesting heuristics, we again leap to the conclusion
![]()
where ![]() ,
, ![]() .
.
The obvious symmetry ![]() is reflected in formula (9),
since changing the sign of x is equivalent to interchanging r and
s. It is also clear that
is reflected in formula (9),
since changing the sign of x is equivalent to interchanging r and
s. It is also clear that
(a) if n+x+y is odd, then r, s are not integers, and
(b) if |x|+y > n, then at least one of r, s is negative,
so that in either of these cases,
![]()
We can prove (9) inductively from the recursion (10), which states that the last step was either N, S, E or W:
![]()
Notice that the sums of the three arguments in the five terms are all of
the same parity. If this is odd, then all the terms are zero. But if
(r,s) are integers, then the corresponding values for the four terms
on the right of (10) are
and if we assume that formula (9) holds with n-1 in place of n, then (10) yields
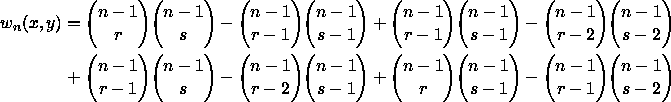
which becomes formula (9) after some more or less tedious manipulation, depending on one's ingenuity or symbol manipulator.
To find ![]() , sum (9) over x:
, sum (9) over x:
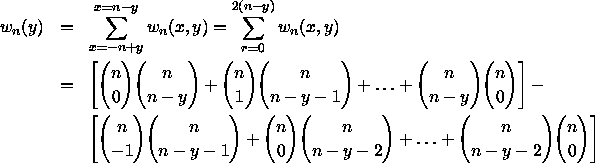
The two brackets are the coefficients of ![]() and of
and of ![]() in
the expansion of
in
the expansion of ![]() , so that
, so that
![]()
which may be rewritten as
![]()
On comparing this with (4) we see that
![]()
the number of odd length one-dimensional walks which finish, of course, at an odd distance from the origin.
In particular, (7) is the same as the number of walks from (0,0) to (n,n+1) which begin with a northward step and do not cross the line joining start to finish, w(2n+1,1), which is
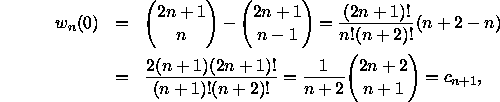
the (n+1)th Catalan number.
Finally, summing (11) from y = 0 to y = n gives (8).
We could ask similar questions concerning walks which do not stray outside the positive quadrant. The numbers of such walks now form a ``Pascal quarter-pyramid'', which is exhibited in Fig. 4.
Figure 4: Layers of a Pascal quarter-pyramid: values of ![]() .
.
The entries in Fig. 4 are given, again without motivation, by
![]()
where ![]() ,
, ![]() as before. Notice
that interchange of x and y keeps s fixed and replaces r by
n-r. So the symmetry
as before. Notice
that interchange of x and y keeps s fixed and replaces r by
n-r. So the symmetry
![]()
follows from the symmetries
![]()
We may prove (12) as we proved (9), since ![]() also satisfies the
relation (10).
also satisfies the
relation (10).
A remarkable coincidence is that
![]()
is the number of inequivalent Hamiltonian rooted maps on 2k vertices (sequence A000356 in [10]) although Tutte [12] doesn't give the formula in terms of Catalan numbers. Is there yet another opportunity for a purely combinatorial proof?
Figure 5: Sums of rows of Fig. 4: values of ![]() .
.
Figure 5 is obtained by summing the rows of Fig. 4, and we may find
![]() , the number of walks in the positive quadrant which finish at
distance y from the x-axis, by summing (12) from x = 0 to x = n-y.
, the number of walks in the positive quadrant which finish at
distance y from the x-axis, by summing (12) from x = 0 to x = n-y.
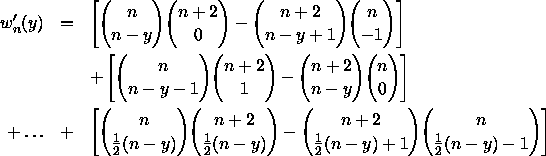
if n-y is even, but with the last term replaced by
![]()
if n-y is odd.
Put n-y = 2k or 2k+1 and
![]()
In particular, if y = 0,
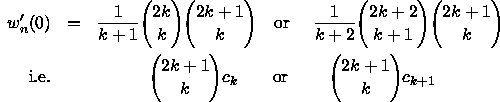
according as n = 2k or n = 2k+1, where ![]() is the k-th
Catalan number.
is the k-th
Catalan number.
(The first few columns of Fig. 5 produce sequences A005558, A005559, A005560, A005561, A005562; and the triangle itself gives A052174.)
For walks in the positive quadrant it is more natural and symmetrical to ask for the numbers of walks which terminate at various distances from the origin, using the ``Manhattan metric'', x+y = n-2s. Figure 6 shows the sums of the diagonals of Fig. 4.
Figure 6: Sums of diagonals of Fig.4: values of ![]() .
.
The entries in Fig. 6 are
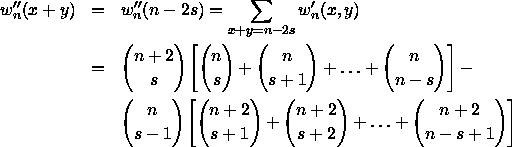
Except for small values of s, the truncated binomial expansions do not seem to have a simple closed form:
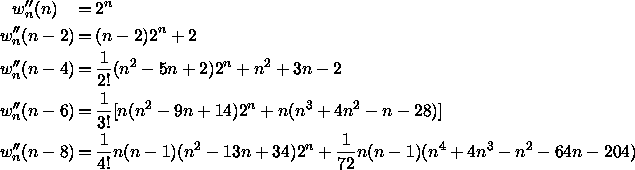
An amusing curiosity is that ![]() (sequences
A036799
and
A000337)
is twice the genus of the
(n+2)-dimensional cube [8, or see Theorem 14 in 3].
(sequences
A036799
and
A000337)
is twice the genus of the
(n+2)-dimensional cube [8, or see Theorem 14 in 3].
The total number of walks, ![]() (A005566)
, the left hand column in Fig. 6, has,
on the other hand, the comparatively simple formula
(A005566)
, the left hand column in Fig. 6, has,
on the other hand, the comparatively simple formula
![]()
which again seems to beg for a simple proof.
The columns in Fig. 6 give sequences A005568 and A005569; the diagonals give A000079, A036799 and A005567; and the triangle itself forms A052175 and A052176.
If there is no restriction on the two-dimensional walks, i.e. if they may wander on either side of the x- and y-axes, then it is fairly easy to see that their number of length n, from (0,0) to (x,y), is
![]()
where r and s are as before, but calculated using the absolute values of x and y.
Of course, the total number of walks of length n is ![]() .
.
Although we certainly haven't found the most aesthetic proofs, the
comparative simplicity of the final results tempts us to ask what
happens in three dimensions. Let ![]() be the number of walks of
n steps, each in a direction N, S, E, W, up, or down, from (0,0,0)
to (x,y,z), which never go below the (x,y)-plane. We will not
attempt to depict the four-dimensional ``Pascal semi-pyramid'', but the
sums of its layers now give
be the number of walks of
n steps, each in a direction N, S, E, W, up, or down, from (0,0,0)
to (x,y,z), which never go below the (x,y)-plane. We will not
attempt to depict the four-dimensional ``Pascal semi-pyramid'', but the
sums of its layers now give ![]() , the number of walks terminating
at height z above the (x,y)-plane, and this satisfies the recurrence
, the number of walks terminating
at height z above the (x,y)-plane, and this satisfies the recurrence
![]()
which may be used to produce the array of Fig. 7.
Each entry in Fig. 7 is the sum of four times the entry immediately above it and the two neighbors of that entry, e.g.
![]()
(The row sums in Fig. 7 give A005573; the columns give A005572, A052177 and A052178; and the triangle itself forms A052179.)
We again suppress the details of discovery of the general formula, and
of its inductive proof: these details seem to be more complicated than
before, and we found no obvious manifestation of the Catalan numbers.
The simplest expression for ![]() that we have so far found
is not in closed form:
that we have so far found
is not in closed form:
![]()
where ![]() and the coefficients
and the coefficients ![]() are of
shape
are of
shape
![]()
although there are, of course, closed form expressions for small values of v:
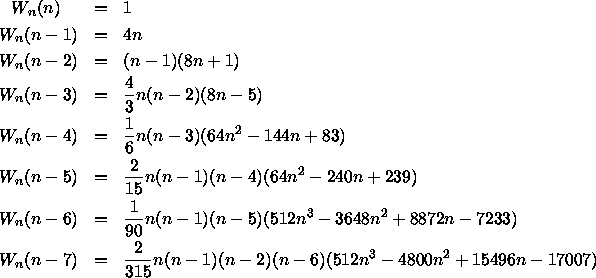
We have not found a closed expression for ![]() , the total number of
walks of n steps which do not go below the (x,y)-plane, nor have we
had an opportunity to examine the paper [5] which may contain such
an expression and may overlap the present paper in other ways. The total
number of n-step walks in d dimensions, without restriction, is, of
course,
, the total number of
walks of n steps which do not go below the (x,y)-plane, nor have we
had an opportunity to examine the paper [5] which may contain such
an expression and may overlap the present paper in other ways. The total
number of n-step walks in d dimensions, without restriction, is, of
course, ![]() .
.
This addendum arises from correspondence with Christian Krattenthaler and Bruce Sagan, and a referee's report on the original (1991) version of this manuscript.
Christian Krattenthaler writes that ``...the classes of lattice paths
you have considered do not seem to have been treated before''. On the
other hand, both he and the referee point out that formula (15) appears
in Theorem 2 in [D1]. The referee also notes that formula (4) is
in [Fe] and that formulas (9), (11), (12), and that for
![]() , follow easily from (15) and the reflexion principle.
However, the exciting news is that Krattenthaler supplies
combinatorial proofs of almost all of the formulas, of the kind appealed
for, and that Bruce Sagan also gives very similar proofs. The
main item that is still missing is a combinatorial proof of the formula(s) for
, follow easily from (15) and the reflexion principle.
However, the exciting news is that Krattenthaler supplies
combinatorial proofs of almost all of the formulas, of the kind appealed
for, and that Bruce Sagan also gives very similar proofs. The
main item that is still missing is a combinatorial proof of the formula(s) for
![]() .
.
The proofs are paraphrased below and also appear in
Richard K. Guy, Christian Krattenthaler and Bruce Sagan, Lattice paths, reflections and dimension-changing bijections, Ars Combinatorica, 34 (1992) 3-15; MR 93i:05008.
See also: Solutions to Problem 1517, Crux Mathematicorum, 17 #4 (Apr 1991) 119--122.
1. Proof of (15). Set up a correspondence between ``NSEW'' paths,
p, and pairs ( ![]() ,
, ![]() ) of ``NE'' paths: if the m-th step
of p is N, S, E, W, then the m-th step of
) of ``NE'' paths: if the m-th step
of p is N, S, E, W, then the m-th step of ![]() is respectively
N, E, E, N, and that of
is respectively
N, E, E, N, and that of ![]() is N, E, N, E. Then the ``NSEW'' paths of
n steps from (0, 0) to (x, y) are in 1-1 correspondence with
pairs (
is N, E, N, E. Then the ``NSEW'' paths of
n steps from (0, 0) to (x, y) are in 1-1 correspondence with
pairs ( ![]() ,
, ![]() ) of ``NE'' paths, where
) of ``NE'' paths, where ![]() runs from (0, 0) to
(r, n-r) and
runs from (0, 0) to
(r, n-r) and ![]() from (0, 0) to (s, n-s), where
from (0, 0) to (s, n-s), where
![]() and
and ![]() as before.
as before.
[Algebraic detail: If the numbers of N, S, E, W steps are respectively a, b, c, d, then n = a+b+c+d, x = c-d, y = a-b, r = b+c, n-r = a+d, s = b+d, n-s = a+c and r, s are as stated.]
But the number of ``NE'' paths from (0, 0) to (k, l) is
![]() , so the number of NSEW paths from (0, 0) to (x, y)
is
, so the number of NSEW paths from (0, 0) to (x, y)
is
![]()
i.e., formula (15).
2. Proof of (9). To count NSEW paths of n steps from (0, 0) to (x, y) which do not go below the x-axis, use the reflexion principle. We must subtract the number of paths which cross the x-axis. Each of these has a first point, say P, for which y = -1. Relect the initial portion OP in the line y = -1, giving a 1-1 correspondence between paths which cross the x-axis and paths from (0, -2) to (x, y). Their number is the same as the total number of paths already counted, except that y is replaced by y+2, i.e., r and s are each decreased by 1. This gives formula (9):
![]()
3. Proof of (12). Reflexion may also be used to count the NSEW paths which stay in the positive quadrant. A second relexion in x = -1 together with the inclusion-exclusion principle shows that this number is
#{paths from (0, 0) to (x, y)} - #{paths from (0, -2) to (x, y)} - #{paths from (-2, 0) to (x, y)} + #{paths from (-2, -2) to (x, y)}
![]()
which easily manipulates into formula (12).
4. Proof of (11). To count the Sands-type paths, p,
which finish at height y, use another correspondence with NE paths,
![]() , of twice the length. If the m-th step of p is N, S, E, W,
then the (2m-1)-th and 2m-th steps of
, of twice the length. If the m-th step of p is N, S, E, W,
then the (2m-1)-th and 2m-th steps of ![]() are respectively
NN,EE,NE,EN. This sets up a bijection between NSEW paths with n steps
from (0, 0) to height y which do not cross the x-axis and NE paths
from (0, 0) to (n-y, n+y) which do not cross the line y = x-1.
To enumerate these, use the reflexion principle again. A path which
crosses the line y = x-1 has a first point Q for which y = x-2.
Reflect the portion OQ of such a path in the line y = x-2. This gives
a correspondence with NE paths of 2n steps from (2, -2) to
(n-y, n+y) whose number is
are respectively
NN,EE,NE,EN. This sets up a bijection between NSEW paths with n steps
from (0, 0) to height y which do not cross the x-axis and NE paths
from (0, 0) to (n-y, n+y) which do not cross the line y = x-1.
To enumerate these, use the reflexion principle again. A path which
crosses the line y = x-1 has a first point Q for which y = x-2.
Reflect the portion OQ of such a path in the line y = x-2. This gives
a correspondence with NE paths of 2n steps from (2, -2) to
(n-y, n+y) whose number is ![]() . This confirms the
formula displayed just before formula (11). To see (11) itself, adjoin a
single N-step to the beginning of path
. This confirms the
formula displayed just before formula (11). To see (11) itself, adjoin a
single N-step to the beginning of path ![]() and again apply the
reflexion principle.
and again apply the
reflexion principle.
Note that if we also adjoin a final E-step to the path ![]() we see
that the number of Sands-type paths with n steps from (0, 0) which
finish on the x-axis is the same as the number of NE walks from
(0, -1) to (n+1, n) which do not cross the line y = x-1, and this
is well-known to be
we see
that the number of Sands-type paths with n steps from (0, 0) which
finish on the x-axis is the same as the number of NE walks from
(0, -1) to (n+1, n) which do not cross the line y = x-1, and this
is well-known to be ![]() .
.
5. Proof of (1). First use the correspondence of 4. to map
p (Sands-type, n steps from (0, 0) to height y, not crossing the
x-axis) onto ![]() (NE path, 2n+1 steps from (0, -1)
to (n-y, n+y), not crossing y = x-1). Consider the last meeting
point of
(NE path, 2n+1 steps from (0, -1)
to (n-y, n+y), not crossing y = x-1). Consider the last meeting
point of ![]() with y = x-1. The next step is an N-step,
which we change to an E-step, obtaining a new path from (0, -1) to
(n-y+1, n+y-1). Repeat this procedure, this time considering the
last meeting point with the line y = x-2. Next consider the line
y = x-3, &c. After y changes we arrive at a path from (0, -1) to
(n, n). Since this sets up a bijection between NE paths of 2n+1
steps starting from (0, -1) and not crossing the line y = x-1, and NE
paths from (0, -1) to (n, n) (last meeting points become first
crossing points!), we obtain the total number of Sands-type paths of n
steps,
with y = x-1. The next step is an N-step,
which we change to an E-step, obtaining a new path from (0, -1) to
(n-y+1, n+y-1). Repeat this procedure, this time considering the
last meeting point with the line y = x-2. Next consider the line
y = x-3, &c. After y changes we arrive at a path from (0, -1) to
(n, n). Since this sets up a bijection between NE paths of 2n+1
steps starting from (0, -1) and not crossing the line y = x-1, and NE
paths from (0, -1) to (n, n) (last meeting points become first
crossing points!), we obtain the total number of Sands-type paths of n
steps,
![]()
A1. D. André, Solution directe du problème résolu par M. Bertrand, C.R. Acad. Sci. Paris 105 (1887) 436-437; Jbuch 19, 200.
[Cf. B1 and Ze.]
A2. George E. Andrews, Catalan numbers, q-Catalan numbers and hypergeometric series, J. Combin. Theory Ser. A 44 (1987) 267-273; MR 88f:05015.
[The Catalan numbers may be defined as solutions to (1) ![]() ,
,
![]() , n > 0. The author introduces a new
q-analog of the Cats via
, n > 0. The author introduces a new
q-analog of the Cats via ![]() ,
,
![]() ...and the
more general numbers
...and the
more general numbers ![]() and gives two proofs of
and gives two proofs of
![]() ,
n > 0. He also establishes the explicit formula
,
n > 0. He also establishes the explicit formula
![]() . He notes that his q-Cats are the
only known q-analog of the Cats which have both a simple
representation as a finite product and satisfy an exact q-analog
of (1). He also interprets
. He notes that his q-Cats are the
only known q-analog of the Cats which have both a simple
representation as a finite product and satisfy an exact q-analog
of (1). He also interprets ![]() and
and ![]() as generating functions of numbers of certain partitions.
Mourad E.H. Ismail]
as generating functions of numbers of certain partitions.
Mourad E.H. Ismail]
B1. T. Bertrand, Solution d'un problème, C.R. Acad. Sci. Paris 105 (1887) 369.
[Cf. A1 and Ze.]
B2. M.T.L. Bizley, Derivation of a new formula for the number of minimal lattice paths from (0,0) to (km,kn) having just t contacts with the line my = nx and having no points above this line; and a proof of Grossman's formula for the number of paths which may touch but do not rise above this line, J. Inst. Actuar., 80 (1954) 55-62; MR 15, 846d.
[Write ![]() for the lattice paths with t contacts as described
in the title and, following G5, write
for the lattice paths with t contacts as described
in the title and, following G5, write
![]()
then the author's new formula may be stated as
![]()
The corresponding formula for ![]() , namely
, namely
![]()
is equivalent to Grossman's formula ...J. Riordan]
[presumably ![]() and the summation is over t.]
and the summation is over t.]
B3. David Blackwell & J.L. Hodges, Elementary path counts, Amer. Math. Monthly, 74 (1967) 801-804; Zbl. 155, 29c.
[Consider a sequence ![]() , ...,
, ..., ![]() with entries
with entries ![]() ,
and let
,
and let ![]() be the partial sums. The authors
furnish an elementary combinatorial proof of two known theorems
concerning the enumeration of such sequences relative to two
parameters: the sum
be the partial sums. The authors
furnish an elementary combinatorial proof of two known theorems
concerning the enumeration of such sequences relative to two
parameters: the sum ![]() , and the lead, or number of indices
i for which both
, and the lead, or number of indices
i for which both ![]() and
and ![]() are non-negative.
H.H. Crapo]
are non-negative.
H.H. Crapo]
Ca. L. Carlitz & J. Riordan, Two element lattice permutation numbers and their q-generalization, Duke Math. J., 31 (1964) 371-388; MR 29 #5752.
[A two-element lattice permutation can be described in a
two-dimensional lattice as a path leading from (0,0) to a point
(m,n) (where ![]() ) with the conditions that the path
has minimum length, viz., m+n, and that it does not contain
points (a,b) with a < b. It can also be described as an
election for two candidates A, B with final vote (n,m),
which is such that none of the partial results gives a majority
for B (in the paper it is less accurately said that all
partial results correctly predict the winner). The number
) with the conditions that the path
has minimum length, viz., m+n, and that it does not contain
points (a,b) with a < b. It can also be described as an
election for two candidates A, B with final vote (n,m),
which is such that none of the partial results gives a majority
for B (in the paper it is less accurately said that all
partial results correctly predict the winner). The number
![]() of such two-element lattice permutations was determined
in 1887 by J. Bertrand [B1, see Ma] as
of such two-element lattice permutations was determined
in 1887 by J. Bertrand [B1, see Ma] as
![]()
The authors consider ![]() and show that
this nth degree polynomial is characterized by the property
that
and show that
this nth degree polynomial is characterized by the property
that ![]() has the form
has the form ![]() , where
, where ![]() is again an nth degree polynomial; in fact,
is again an nth degree polynomial; in fact,
![]() . A number of relations are derived
for the generating function
. A number of relations are derived
for the generating function ![]() .
.
The authors consider these formulas as the special case (q = 1) of
a q-generalization. They define the nth degree polynomial
![]() by the condition that there exist
by the condition that there exist ![]() , ...,
, ..., ![]() such that
such that
![]()
where ![]() denotes
denotes ![]() . The coefficients
. The coefficients ![]() of this polynomial are studied in several ways.
of this polynomial are studied in several ways.
{The reviewer remarks that ![]() has the following
combinatorial interpretation: It is the sum of all
has the following
combinatorial interpretation: It is the sum of all
![]() , where
, where ![]() , ...,
, ..., ![]() are integers
subject to the conditions
are integers
subject to the conditions ![]() ,
,
![]() , ...,
, ..., ![]() .} N.G. de Bruijn]
.} N.G. de Bruijn]
1. Arthur Cayley, On the partitions of a polygon, Proc. London Math. Soc. 22 (1891) 237-262 = Coll. Math. Papers 13 (1897) 93-113.
Ci. J. Cigler, Some remarks on Catalan families, European J. Combin., 8 (1987) 261-267; MR 89a:05010.
[The author first gives a simple proof that the r-Catalan number
![]() is the number of ways of parenthesizing
an r-ary product of (r-1)n+1 factors, or equivalently, the
number of r-ary trees with n points. Next he shows, using a
variant of the Dvoretzky-Motzkin cycle lemma, that the number of
r-ary trees with n points and
is the number of ways of parenthesizing
an r-ary product of (r-1)n+1 factors, or equivalently, the
number of r-ary trees with n points. Next he shows, using a
variant of the Dvoretzky-Motzkin cycle lemma, that the number of
r-ary trees with n points and ![]() edges from a point to its
ith subtree, where
edges from a point to its
ith subtree, where ![]() , is
, is
![]() . From this
formula he deduces that the number of nonnegative paths from (0,0)
to (rn,0) with k+1 peaks, using the steps (1,1) and (1,1-r),
is the generalized Runyon number
. From this
formula he deduces that the number of nonnegative paths from (0,0)
to (rn,0) with k+1 peaks, using the steps (1,1) and (1,1-r),
is the generalized Runyon number
![]() . Finally he discusses the
connexion between these results, noncrossing partitions and
Sperner's theorem. Ira Gessel]
. Finally he discusses the
connexion between these results, noncrossing partitions and
Sperner's theorem. Ira Gessel]
C0. E. Csáki, On the number of intersections in the one-dimensional random walk, Magyar Tud. Akad. Mat. Kutató Int. Közl., 6 (1961), 281-286; MR 26 #5642.
[Consider a discrete one-dimensional random walk in which, with the
usual notation, ![]() , and let
, and let
![]() be the number of passages through the point k
in a walk of j steps. Write
be the number of passages through the point k
in a walk of j steps. Write ![]() . The
following results are proved. (i)
. The
following results are proved. (i)
![]() for
for ![]() , and is
, and is ![]() if l=0. (ii) For
fixed positive even k,
if l=0. (ii) For
fixed positive even k,
![]() . (iii) For fixed positive odd k,
. (iii) For fixed positive odd k,
![]() . The proofs are entirely
combinatorial. J. Gillis]
. The proofs are entirely
combinatorial. J. Gillis]
C1. Endre Csáki & Sri Gopal Mohanty, Some joint distributions for conditional random walks, Canad. J. Statist. 14 (1986) 19-28; MR 87k:60168.
[Joint distributions of maxima, minima and their indices are determined for certain conditional random walks called Bernoulli excursion and Bernoulli meander. The distribution of the local time of these processes is treated by a generating function technique. Limiting distributions are also given, providing some partial results for Brownian excursion and meander. For instance the authors conjecture the joint limit distributions of the local time and the maximum for these two processes. Similar investigations are carried out for the unconditional random walk and for the Bernoulli bridge. G. Louchard (Brussels)]
C2. Endre Csáki, Sri Gopal Mohanty & Jagdish Saran, On random walks in a plane, Ars Combin. 29 (1990) 309-318.
C3. E. Csáki & I. Vincze, On some problems connected with the Galton test, Magyar Tud. Akad. Mat. Kutató Int. Közl., 6 (1961), 97-109; MR 26 #3138.
[The authors give the probability of the number of waves relative
to the horizontal line in the sequence of the sum ![]() of the
first i members of a random sequence of n +1's and n -1's,
where i = 1, 2, ..., 2n, with limiting distribution in
of the
first i members of a random sequence of n +1's and n -1's,
where i = 1, 2, ..., 2n, with limiting distribution in
![]() and the joint probability distribution for
the number of waves mentioned above and the Galton statistic
in the sequence with the limiting distribution. Then they give
the joint probability distribution for the number of waves
relative to the height k > 0 from the horizontal line and the
length of time spent above this height expressed by the number of
positive members in the well-defined sequence with the limiting
distribution. They suggest the statistical tests based on these
theorems in a two-sample problem. C. Hayashi (Tokyo)]
and the joint probability distribution for
the number of waves mentioned above and the Galton statistic
in the sequence with the limiting distribution. Then they give
the joint probability distribution for the number of waves
relative to the height k > 0 from the horizontal line and the
length of time spent above this height expressed by the number of
positive members in the well-defined sequence with the limiting
distribution. They suggest the statistical tests based on these
theorems in a two-sample problem. C. Hayashi (Tokyo)]
C4. E. Csáki & I. Vincze, On some distributions connected with the arc-sine law (Russian summary), Magyar Tud. Akad. Mat. Kutató Int. Közl., 8 (1963), 281-291; MR 29 #4078.
[Several results extending those of the reviewer and Feller, and
generalized by E.S. Andersen, are given. The combinatorial formulae
are obtained by one-to-one correspondence, from which asymptotic ones
are computed. For instance, let ![]() , i = 0, 1, 2, ..., be the
successive sums in the coin-tossing game with stakes
, i = 0, 1, 2, ..., be the
successive sums in the coin-tossing game with stakes ![]() ,
, ![]() ,
and let
,
and let ![]() denote the number of indices i
denote the number of indices i
![]() for which either
for which either ![]() or
or ![]() but
but
![]() , where k is a non-negative integer; then
, where k is a non-negative integer; then
![]()
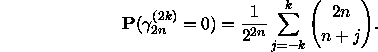
K.L. Chung
De. Nachum Dershowitz & Schmuel Zaks, The cycle lemma and some applications, European J. Combin., 11 (1990) 35-40.
D1. Duane W. DeTemple & Jack M. Robertson, Equally likely fixed length paths in graphs, Ars Combin. 17 (1984) 243-254; MR 86h:60103.
[Gives equation (15) in the original paper.] [The authors investigate the unique stochastic process whose realizations are the set of paths of given length joining two given vertices of a given graph and which has the property that all such paths are equally likely to occur. There is an application to the design of experiments. G.R. Grimmett (Bristol)]
D2. Duane W. DeTemple, C.H. Jones & Jack M. Robertson, A correction for a lattice path counting formula, Ars Combin. 25 (1988) 167-170; MR 89i:05017.
[Gives equation (15) in the original paper.] [In D1, DeT & R gave the formula
![]()
for the number of lattice paths in the plane length d, with unit steps in the positive and negative coordinate directions, starting at the origin and ending at (a,b) which touch the line x = ky only at the initial point. In the present paper the authors note that this formula is correct if d = a+b, a-kb = 1, or k = 1; in other cases it is an upper bound.
The authors use the method of cyclic permutation or ``penetrating analysis'' due to Dv. A method which yields an exact, but complicated, formula for this kind of problem was described in G1. Ira Gessel]
2. C. Domb, On the theory of cooperative phenomena in crystals, Advances in Physics 9 (1960) 149-361.
Dv. A. Dvoretzky & Th. Motzkin, A problem of arrangements, Duke Math. J., 14 (1947) 305-313; MR 9, 75e.
[...In an election, candidates P and Q receive
p and q votes, respectively; required the probability that the
ratio of the ballots for P to those for Q will, throughout
the counting, be larger than (larger than or equal to) ![]() .]
.]
E. O. Engleberg, On some problems concerning a restricted random walk, J. Appl. Probability, 2 (1965) 396-404; MR 32 #475.
[The restricted random walk in question is on a line (vertical for
convenience) with unit steps up and down and prescribed numbers
of each. In the terminology of Feller [Fe] such a walk is a
polygonal path from (0,0) to (n+m,n-m); it is also in one-to-one
correspondence with a two-candidate election return with final vote
(n,m). In election return terms, the author's main results are
as follows: If c(x;n,m) is the enumerator of election returns
with final vote (n,m), ![]() , by number of changes of lead,
if t(x;n,m) is the corresponding enumerator by number of ties,
then
, by number of changes of lead,
if t(x;n,m) is the corresponding enumerator by number of ties,
then ![]() , n > m,
c(x;n,n) = 2c(x;n,n-1),
, n > m,
c(x;n,n) = 2c(x;n,n-1), ![]() ,
where
,
where
![]()
The numbers ![]() are the
oldest ballot numbers. (For n < m, the enumerators in the two
cases, by symmetry, are those above with n and m
interchanged, a result not noticed by the author.) These results
are used with obvious summations to verify the results of Feller
[Fd] for the enumeration of unrestricted random walks by
number of axis crossings and by number of zeros (of their
polygonal paths). Also the limiting distribution functions of
tie returns (n = m) are determined. Finally, the application
of the results to the comparison of two empirical distributions
is sketched.
are the
oldest ballot numbers. (For n < m, the enumerators in the two
cases, by symmetry, are those above with n and m
interchanged, a result not noticed by the author.) These results
are used with obvious summations to verify the results of Feller
[Fd] for the enumeration of unrestricted random walks by
number of axis crossings and by number of zeros (of their
polygonal paths). Also the limiting distribution functions of
tie returns (n = m) are determined. Finally, the application
of the results to the comparison of two empirical distributions
is sketched.
{In equation (11) there are two typographical slips whose corrections will probably be evident to most readers.} J. Riordan]
Fd. W. Feller, The number of zeros and of changes of sign in a symmetric random walk, Enseignement Math.(2), 3 (1957) 229-235; MR 20 #4329.
[Let ![]() where the
where the ![]() are independent and
assume the values
are independent and
assume the values ![]() with probability
with probability ![]() . The author
derives for this symmetric random walk explicit formulas for the
probability distribution of the number of returns to the origin,
the number of changes of sign and other related quantities. The
derivations are of a very elementary nature and the paper is
self-contained. A more exhaustive treatment appears in Chapter III
of the 2nd ed. of Fe (1957). J.L. Snell]
. The author
derives for this symmetric random walk explicit formulas for the
probability distribution of the number of returns to the origin,
the number of changes of sign and other related quantities. The
derivations are of a very elementary nature and the paper is
self-contained. A more exhaustive treatment appears in Chapter III
of the 2nd ed. of Fe (1957). J.L. Snell]
Fe. W. Feller, An Introduction to Probability Theory and its Applications, Vol. 1, Wiley, 1968, p. 73
[The reference gives equation (4) in the original paper.
On p. 82 it is noted that
![]() is the number of paths of length
2n with exactly 2k steps lying above y = x. On p. 96 is given a
bijection between paths from (0,0) to (k,k) and paths of length
2k which do not pass below y = x.]
is the number of paths of length
2n with exactly 2k steps lying above y = x. On p. 96 is given a
bijection between paths from (0,0) to (k,k) and paths of length
2k which do not pass below y = x.]
Fl. Philippe Flajolet, Combinatorial aspects of continued fractions, Discrete Math., 32 (1980) 125-161; Ann. Discrete Math., 9 (1980) 217--222; MR 82f:05002ab.
[Referred to in review of G3.]
Fu. J. Fürlinger & J. Hofbauer, q-Catalan numbers, J. Combin. Theory Ser. A, 40 (1985) 248-264; MR 87e:05017.
[The Catalan numbers ![]() are defined by
are defined by
![]() and satisfy
and satisfy
![]() and
and
![]() . This paper surveys
several q-analogs of the Catalan numbers. The authors
first consider the q-Catalan numbers of Ca. These
satisfy
. This paper surveys
several q-analogs of the Catalan numbers. The authors
first consider the q-Catalan numbers of Ca. These
satisfy
![]()
and
![]()
There is no simple explicit formula for ![]() , but there is
a combinatorial interpretation in terms of inversions of certain
0-1 sequences.
, but there is
a combinatorial interpretation in terms of inversions of certain
0-1 sequences.
Next the authors consider the q-Catalan numbers given by
![]()
in which the terms are q-Runyon numbers. Here one defines
![]() and
and
![]() is the
q-binomial coefficient. For
is the
q-binomial coefficient. For ![]() these reduce to
these reduce to
![]() . These q-Catalan numbers satisfy
. These q-Catalan numbers satisfy
![]()
where ![]() , and they have a
combinatorial interpretation in terms of major indices and
descents of 0-1 sequences.
, and they have a
combinatorial interpretation in terms of major indices and
descents of 0-1 sequences.
A generalization which includes both types of q-Catalan numbers is considered next. These satisfy
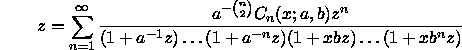
and are also given a combinatorial interpretation. They also include as a special case the q-Catalan numbers studied in Po. Ira Gessel]
Fv. Harry Furstenberg, Algebraic functions over finite fields, J. Algebra, 7 (1967) 271-277; MR 35 #6655.
[Referred to in review of G1.]
G1. Ira M. Gessel, A factorization for formal Laurent series and lattice path enumeration, J. Combin. Theory Ser. A 28 (1980) 321-327; MR 81j:05012.
[A powerful and striking factorization for certain formal Laurent series is proved, namely that the series is a product of a constant, a series in only negative powers and a series in only positive powers. Lagrange's formula for series reversion is treated as an application. Other applicationa are to the problems of enumerating restricted lattice paths (a novel interpretation of Laurent series in combinatorial theory) and to H. Furstenberg's theorem [Fv] that the diagonal of a rational power series in two variables is algebraic (giving a new formal method of showing that certain series are algebraic. D.G. Rogers]
G2. Ira M. Gessel, A probabilistic method for lattice path enumeration, J. Statist. Plann. Inference 14 (1986) 49-58; MR 87h:05017.
[Some lattice path counting problems may be converted into problems of deriving distributions on random walks which give rise to functional equations. Solutions of these equations provide a probabilistic approach to the lattice path enumeration problems. The approach is illustrated by a few examples. Sri Gopal Mohanty]
G3. Ira M. Gessel, A combinatorial proof of the multivariable Lagrange inversion formula, J. Combin. Theory Ser. A 45 (1987) 178-195; MR 88h:05011.
[Using the exponential generating function, the author gives a combinatorial proof of one form of the multivariable Lagrange inversion formula (MLIF). An outline of the proof is: (1) interpret the defining functional relations as generating functions for colored trees, (2) interpret the desired coefficient as the generating function for functions from a set to a larger set, (3) decompose the functional digraph from (2) into two types of connected components, whose generating functions give the MLIF. Labelle had given such a proof in one variable [L].
The author also gives a useful survey of forms of the MLIF given by Jacobi, Stieltjes, Good, Joni, and Abhyankar. He shows that Jacobi's form implies Good's form and gives a simple form generalizing that of Stieltjes, Joni, and Abhyankar.
The paper includes some historical information on the Jacobi formula for matrices, det exp A = exp trace A. Dennis Stanton]
Go. Henry W. Gould, Final analysis of Vandermonde's convolution, Amer. Math. Monthly, 64 (1957) 409-415; MR 19, 379c.
[Referred to in review of Ra.]
GJ. I.P. Goulden & D.M. Jackson, Path generating functions and continued fractions, J. Combin. Theory Ser. A, 41 (1986) 1-10; MR 87i:05020.
[The authors consider paths along the nonnegative integers in which each step consists of an increase of altitude of 1 (a rise), 0 (a level), or -1 (a fall). The paths are weighted to record the number of rises and levels at each altitude. The main result of the paper answers the following question: What is the sum of the weights of all paths with given initial and terminal altitudes, and with given bounds on maximum and minimum altitudes? The answer is expressed in terms of continued fractions and extends P. Flajolet's combinatorial theory of continued fractions [Fl]. Some classical identities for continued fractions are obtained as corollaries. Ira Gessel]
G4. Dominique Gouyou-Beauchamps & G. Viennot, Equivalence of the two-dimensional directed animal problem to a one-dimensional path problem, Adv. in Appl. Math., 9 (1988) 334-357; MR 90c:05009.
[A set P of lattice points in the plane is called a directed animal if there is a subset of P, whose elements are called root points, such that the root points lie on a line perpendicular to the line y=x, and every point of P can be reached from a root point by a path in P using only north and east steps. This paper is concerned with the enumeration of compact-rooted animals, which are animals in which the root points are consecutive. Animals which differ only by translation are considered to be equivalent.
The main result is a bijection between compact-rooted animals
of size n+1 and paths of length n on the integers, with
steps +1, 0 and -1. This bijection implies that there are
![]() compact-rooted animals of size n+1. Moreover the
bijection allows the compact-rooted animals to be counted
according to the number of root points. Further consequences are
that the generating function for directed animals with one root
point is
compact-rooted animals of size n+1. Moreover the
bijection allows the compact-rooted animals to be counted
according to the number of root points. Further consequences are
that the generating function for directed animals with one root
point is ![]() and that the
number of directed animals of size n rooted at the origin
and contained in the first octant
and that the
number of directed animals of size n rooted at the origin
and contained in the first octant ![]() is the
Motzkin number
is the
Motzkin number ![]() .
.
The paper also contains many references to work by physicists on problems of counting animals, which arise in studying thermodynamic models for critical phenomena and phase transitions. Ira Gessel]
G5. Howard D. Grossman, Fun with lattice points, Scripta Math., 15 (1945) 79-81; MR 12, 665d.
[Suppose an election results in km votes for A and kn for B. In how many orders may votes be cast so that A's vote is always at least m/n times B's? The author gives without proof the formula
![]()
with ![]() ,
, ![]() and the sum over all partitions of k. He also gives a short
introduction to enumerations in three-dimensional and derives a
solution to a corresponding election problem, noting its
agreement with MacMahon's. J. Riordan]
and the sum over all partitions of k. He also gives a short
introduction to enumerations in three-dimensional and derives a
solution to a corresponding election problem, noting its
agreement with MacMahon's. J. Riordan]
H1. B.R. Handa & Sri Gopal Mohanty, Enumeration of higher-dimensional paths under restrictions, Discrete Math. 26 (1979) 119-128; MR 81b:05012.
[The authors consider the problem of counting lattice paths in k-dimensional space under restrictions. They obtain k-dimensional analogs of the familiar results in two dimensions. D.P. Roselle]
H2. B.R. Handa & Sri Gopal Mohanty, On a property of lattice paths, J. Statist. Plann. Inference 14 (1986) 59-62; MR 87i:05023.
[The authors give an algebraic discussion of the implications on lattice paths of the following fact: increasing sequences of integers such that the jth is at least b(j) greater than the (j-1)st, and is at most a(j), are in one-to-one correspondence to increasing sequences such that the jth is at most a(j) minus the sum of the first j b(k)'s. D.J. Kleitman]
3. Frank Harary, Topological concepts in graph theory, in Harary and Beineke, A Seminar on Graph Theory, Holt, Reinhart & Winston, New York & London, 1967, pp.13-17.
Hi. Terrell L. Hill, Steady-state kinetics of a linear array of interlocking reactions, Statistical Mechanics & Statistical Methods in Theory and Applications (Rochester NY), Plenum, New York, 1977, pp. 521-577; MR 57 #15112.
[Referred to in review of Sh; the MR reference gives no further information.]
J. André Joyal, Une théorie combinatoire des séries formelles, Adv. in Math., 42 (1981) 1-82; MR 84d:05025.
[``We present a combinatorial theory of formal power series. The combinatorial interpretation of formal power series is based on the concept of species of structures. A categorical approach is used to fomulate it. A new proof of Cayley's formula for the number of labelled trees is given as well as a new combinatorial proof (due to G. Labelle) of Lagrange's inversion formula. Pólya's enumeration theory of isomorphism classes of structures is entirely renewed. Recursive methods for computing cycle index polynomials are described. A combinatorial version of the implicit function theorem is stated and proved. The paper ends with general considerations on the use of coalgebras in combinatorics.'']
K. S. Karlin & G. McGregor, Coincidence probabilities, Pacific J. Math., 9 (1959) 1141-1164; MR 22 #5072.
[Among Gessel's references, but may be marginal; cf. immediately preceding paper and review.]
4. T.P. Kirkman, On the k-partitions of the r-gon and r-ace, Phil. Trans. 147 (1857) 225.
Kl. Daniel Kleitman, A note on some subset identities, Studies in Appl. Math., 54 (1975) 289-292; MR 56 #8386.
[Gives combinatorial proof of
![]()
# 19 of the ``Erdös-Pósa'' problems - see Mi.]
5. Christian Krattenthaler, Counting lattice paths with a linear boundary. I. Österreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 198 (1989) 87-107.
K1. Christian Krattenthaler, Enumeration of lattice paths and generating functions for skew plane partitions, Manuscripta Math., 63 (1989) 129-155..
K2. G. Kreweras & H. Niederhausen, Solution of an enumerative problem connected with lattice paths, European J. Combin., 2 (1981) 55-60; MR 82d:05014.
[The authors consider lattice paths of p horizontal and q vertical steps from (0,q) to (p,0). Let W(C) denote the number of paths below C in the dominance partial ordering. The authors prove
![]()
S.G. Williamson]
6. Mike Kuchinski, Catalan Structures and Correspondences, M.Sc. thesis, West Virginia University, Morgantown WV 26506, 1977.
L. Gilbert Labelle, Une nouvelle démonstration combinatoire des formules d'inversion de Lagrange, Adv. in Math., 42 (1981) 217-247; MR 83e:05016.
[The purpose of this paper is to examine connexions between two classical results -- the Lagrange inversion formula for power series and Cayley's formula for the number of labelled trees on n vertices -- in the light of the combinatorial theory of formal series recently presented by J and founded on the notion of ``species of structures''. Some combinatorial operations are defined over species and correspond to analytic operations over their generating functions: hence, properties of the operations over species yield identities for formal series. The authors introduce two canonical constructions which associate a new species -- ``arborescence R-enrichie'' and ``endofonction R-enrichie'', respectively -- to any given species R and proves some deep isomorphism results. These yield, as simple corollaries, some generalized versions of Cayley's formula and the Lagrange inversion formula. Andrea Brini]
L1. Jacques Labelle & Yeong-Nan Yeh, Dyck paths of knight moves, Discrete Appl. Math., 24 (1989) 213-221; MR 90g:05017.
[This paper enumerates lattice paths from the origin to a point along the x-axis which do not go below the x-axis, where the allowable moves are knight moves from left to right. The resulting generating function satisfies a fourth-degree polynomial equation. This compares with so-called Dyck paths, where the allowable moves are one-step diagonal moves to the right. In this classical case the resulting generating function satisfies a quadratic polynomial equation, whose solution yields the Catalan number generating function.
The authors apply their methods to paths with (r,s) knight moves, and obtain polynomial equations of higher degree. Dennis White]
L2. Jacques Labelle & Yeong-Nan Yeh, Generalized Dyck paths, Discrete Math., 82 (1990) 1-6.
L3. Jack Levine, Note on the number of pairs of non-intersecting routes, Scripta Math. 24 (1959) 335-338; Zbl. 93 13a.
[Soit 2 permutations ![]() et
et ![]() de péléments a et q éléments b, p+q=n. Si le nombre
des a est différent du nombre des b dans chaque paire de
séquences partielles correspondantes
de péléments a et q éléments b, p+q=n. Si le nombre
des a est différent du nombre des b dans chaque paire de
séquences partielles correspondantes ![]() et
et
![]() pour k=1, 2, ..., n-1, les permutations
sont dites une paire de permutations non intersectantes, pour une
raison qui provient d'une interprétation graphique. Les 2 paires
pour k=1, 2, ..., n-1, les permutations
sont dites une paire de permutations non intersectantes, pour une
raison qui provient d'une interprétation graphique. Les 2 paires
![]() et
et ![]() sont à considérer comme
équivalentes. L'A. obtient le nombre suivant des paires
distinctes de telles permutations de p éléments a et q
éléments b, p+q=n,
sont à considérer comme
équivalentes. L'A. obtient le nombre suivant des paires
distinctes de telles permutations de p éléments a et q
éléments b, p+q=n,
![]() , 0 < p < n,
0 < q < n. S. Bays]
, 0 < p < n,
0 < q < n. S. Bays]
Li. N. Linial, A new derivation of the counting formula for Young tableaux, J. Combin. Theory Ser. A, 33 (1982) 340-342; MR 83m:05016.
[The well-known hook length formula for the number of standard Young tableaux of a given shape can be written in determinantal form (Frobenius) [see, e.g., D.E. Knuth, The Art of Computer Programming, Vol. 3, pp. 60-63, Addison-Wesley, 1973]. A short proof of this result is given by observing that the expansion of the determinant yields an alternating sum of mutinomial coefficients which obviously satisfies the difference equation for the numbers in question, together with the initial conditions. Volker Strehl]
Ly. R.C. Lyness, Al Capone and the death ray, Math. Gaz., 25 (1941) 283-287.
Ma. Major P.A. MacMahon, Combinatory Analysis, Vol. I, Section III, Chapter V, Cambridge Univ. Press, Cambridge, 1915.
[Referred to in review of Ze and perhaps G5.]
Mi. E.C. Milner, Louis Pósa -- a mathematical prodigy, Nabla, Bull. Malayan Math. Soc., 7 (1960) 61-64; Solutions to the Erdős-Pósa problems I, II, ibid., 107-112, 154-159.
[Problem 19 was to prove the identity mentioned under Kl.]
M1. Sri Gopal Mohanty, Lattice Path Counting and Applications. Probability and Mathematical Statistics. Academic Press, 1979, xi+185 pp.
[Page 2 gives the reflexion principle, whereby equations (9), (11), (12) and the formula at the foot of p. 8 of the original paper all follow from equation (15).]
M2. Sri Gopal Mohanty, On some generalization of a restricted random walk, Studia Sci. Math. Hungar., 3 (1968) 225-241; MR 39 #1022.
[The author considers the paths of a restricted random walk starting
from the origin, which at each step moves either one unit to the right
or ![]() (positive integer) units to the left, and reaches the point
(positive integer) units to the left, and reaches the point
![]() in m+n steps. Random walks are considered schematically by
representing each movement of the particle to the right or to the left
by a horizontal or a vertical unit so that the restricted random walk
corresponds to the minimal lattice paths the particle describes
from the origin to (m,n). Expressions are obtained for total numbers
of distinct paths under certain further conditions as follows. For
a given path, say C, of such a random walk the total number of
paths is found which, after each step, do not lie to the left of the
corresponding point of C, and which touch C in a prescribed way
in exactly r of the last s left steps. Expressions are obtained
also for the number of paths crossing r times (but not necessarily
reaching) a point
in m+n steps. Random walks are considered schematically by
representing each movement of the particle to the right or to the left
by a horizontal or a vertical unit so that the restricted random walk
corresponds to the minimal lattice paths the particle describes
from the origin to (m,n). Expressions are obtained for total numbers
of distinct paths under certain further conditions as follows. For
a given path, say C, of such a random walk the total number of
paths is found which, after each step, do not lie to the left of the
corresponding point of C, and which touch C in a prescribed way
in exactly r of the last s left steps. Expressions are obtained
also for the number of paths crossing r times (but not necessarily
reaching) a point ![]() , for the number of paths reaching
, for the number of paths reaching
![]() , r times, and concerning the joint distribution of the
numbers of times and steps in the region to the right of
, r times, and concerning the joint distribution of the
numbers of times and steps in the region to the right of ![]() .
The last is shown to lead to a result connected with a ballot
theorem of L. Takács [T]. The author mentions also related
results due to E. Csáki [C0], E. Csáki & I. Vincze
[C3, C4], K. Sen [Se] and O. Engleberg [E].
C.J. Ridler-Rowe]
.
The last is shown to lead to a result connected with a ballot
theorem of L. Takács [T]. The author mentions also related
results due to E. Csáki [C0], E. Csáki & I. Vincze
[C3, C4], K. Sen [Se] and O. Engleberg [E].
C.J. Ridler-Rowe]
7. Athanasios Papoulis, A new method of inversion of the Laplace transform, Q. App. Math. 14 (1957) 405-414; MR 18, 602e.
[Finds Legendre coefficients; done earlier by Widder, Duke Math. J., 1 (1935) 126-136; and by Shohat ibid., 6 (1940) 615-626; MR 2, 98.]
P. J. Peacock, On ``Al Capone and the Death Ray'', Note 1633 Math. Gaz., 26 (1942) 218-219.
[See note under Ly.]
Po. G. Pólya, On the number of certain lattice polygons, J. Combin. Theory 6 (1969) 102-105; MR 38 #4329.
[A closed polygon without double points that consists of segments of length one joining neighboring lattice points is called a lattice polygon. Two lattice polygons are considered as not different if and only if there exists a parallel translation superposing one to the other. The number of ``different lattice polygons'' is indicated by dlp. A closed plane curve without double points is termed convex with respect to the direction d if for the intersection of the closed domain surrounded by the curve with any straight line of direction d, only three cases are possible: The intersection is either the empty set, or consists of just one point or of just one segment. A curve is convex in the usual sense if and only if it is convex with respect to all directions [a square is not convex under this strict definition -- RKG].
Let ![]() denote the number of dlp convex with respect to the
vertical direction with area m,
denote the number of dlp convex with respect to the
vertical direction with area m, ![]() the number of dlp
convex with respect to the
the number of dlp
convex with respect to the ![]() direction with
perimeter 2n, and
direction with
perimeter 2n, and ![]() the number of dlp convex with
respect to the
the number of dlp convex with
respect to the ![]() direction with area
m and perimeter 2n; evidently
direction with area
m and perimeter 2n; evidently ![]() . In this paper
explicit expressions are given for the numbers
. In this paper
explicit expressions are given for the numbers ![]() ,
, ![]() and
and
![]() . For example,
. For example,
![]() ,
, ![]() . The proofs
of the results stated will be presented in a subsequent paper.
A.L. Whiteman]
. The proofs
of the results stated will be presented in a subsequent paper.
A.L. Whiteman]
Ra. George N. Raney, Functional composition patterns and power series reversion. Trans. Amer. Math. Soc., 94 (1960) 441-451; MR 22 #5584.
[Let ![]() ,
, ![]() , ...be an infinite sequence of natural numbers
0, 1, 2, ..., such that
, ...be an infinite sequence of natural numbers
0, 1, 2, ..., such that ![]() is finite. The author defines
the numbers
is finite. The author defines
the numbers ![]() combinatorially and shows that
combinatorially and shows that
![]()
where ![]() ,
,
![]() , and L = 1 if m = n = 0. He then
derives some identities involving the numbers L, and uses them
to prove a Lagrange inversion formula on formal power series and
a convolution formula given by Go. Rimhak Ree]
, and L = 1 if m = n = 0. He then
derives some identities involving the numbers L, and uses them
to prove a Lagrange inversion formula on formal power series and
a convolution formula given by Go. Rimhak Ree]
8. Gerhard Ringel, Färbungsprobleme auf Flächen und Graphen, VEB Deutscher Verlag der Wissenschaften, Berlin, 1959.
R1. Don Rawlings, The Euler-Catalan identity, European J. Combin., 9 (1988) 53-60; MR 89g:05017.
[This paper is an attempt to unify the various generalizations of Catalan and Eulerian numbers by using q-theory. The author denotes the generating function for permutations by descents, major index, inversions and patterns by
![]()
Denoting ![]() , the author shows that the recurrence
, the author shows that the recurrence
![]()
holds. Defining C(n;t,q,p)=A(n;t,q,p,0,1) and K(n;t,q,p)=A(n;t,q,p,1,0), the author deduces recurrences for C and K from which two classic q-Catalan numbers defined by Ca follow by taking t = q = 1. Taking u = 1, v = 1 in (**) leads to a new recurrence involving E(n;t,q,p) = A(n;t,q,p,1,1) which defines generalized Eulerian numbers. A conjecture involving the q-Catalan numbers is posed at the end of Section 5. R.N. Kalia]
R2. John Riordan, Combinatorial Identities,
9. Bill Sands, Problem 1517*, Crux Mathematicorum 16 #2 (Feb. 1990) 44.
Se. Kanwar Sen, On some combinatorial relations concerning the symmetric random walk, Magyar Tud. Akad. Mat. Kutató Int. Közl., 9 (1964), 335-357; MR 33 #6715.
[The author considers sequences
![]() of n+k 1's
and n-k -1's, in other words the polygonal paths from (0,0) to
(2n,2k) through the points
of n+k 1's
and n-k -1's, in other words the polygonal paths from (0,0) to
(2n,2k) through the points ![]() with
with
![]() in a rectangular
coordinate-system, where each possible array (path) has the same
probability. In connexion with this restricted random walk, there are
joint distribution laws and joint limiting distribution laws
determined ofr the number of intersections (number of changes of
sign of the
in a rectangular
coordinate-system, where each possible array (path) has the same
probability. In connexion with this restricted random walk, there are
joint distribution laws and joint limiting distribution laws
determined ofr the number of intersections (number of changes of
sign of the ![]() ) and the number of positive steps, as well as for
the number of intersections at the height r (the number of
changes of sign of
) and the number of positive steps, as well as for
the number of intersections at the height r (the number of
changes of sign of ![]() ) and the number of steps above the
height r. Applying the results obtained, the author proves
some known relations for the unrestricted case also. The proofs of
the theorems are of a combinatorial character, some of them
involving one-to-one correspondences of paths. The paper has
some points in common with E. I. Vincze]
) and the number of steps above the
height r. Applying the results obtained, the author proves
some known relations for the unrestricted case also. The proofs of
the theorems are of a combinatorial character, some of them
involving one-to-one correspondences of paths. The paper has
some points in common with E. I. Vincze]
Sh. Louis W. Shapiro, A lattice path lemma and an application in enzyme kinetics, J. Statist. Plann. Inference 14 (1986) 115-122; MR 87j:05021.
[Consider the rectangular lattice from (0,0) to (a,b). Choose
z integers ![]() and
z integers
and
z integers ![]() , and place stones
on the squares
, and place stones
on the squares ![]() , ...,
, ..., ![]() . The author first
shows that if the integers are chosen randomly, and a random path
from (0,0) to (a,b) with unit steps east and north is chosen,
then the probability that the path passes beneath all the stones
is 1/(z+1).
. The author first
shows that if the integers are chosen randomly, and a random path
from (0,0) to (a,b) with unit steps east and north is chosen,
then the probability that the path passes beneath all the stones
is 1/(z+1).
The author next considers a model for enzyme kinetics closely related to that studied by Hi and by SZ. In these models the states are all 0-1 sequences of length M. Each 0 or 1 represents an enzyme, which is either reduced (1) or oxidized (0). The transition rules essentially allow a 01 subsequence to become 10. Using the result of the first part of the paper, the author computes the steady-state distribution under transition probabilities which are different from those used in the earlier papers. Ira Gessel]
SZ. Louis W. Shapiro & Doron Zeilberger, J. Math. Biol., 15 (1982) 351-357; MR 84f:92011.
[The authors investigate a continuous time Markov chain modelling
the diffusion of a ligand across a membrane. The states of the
chain are strings of 0's and 1's of length M and the transitions
are ![]() ,
,
![]() ,
,
![]() , where all the transition rates are equal.
The authors give a formula for the steady state probabilities that
the rth component of the string is zero. Petr Kürka]
, where all the transition rates are equal.
The authors give a formula for the steady state probabilities that
the rth component of the string is zero. Petr Kürka]
10. N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences.
Su. Robert A. Sulanke, A recurrence restricted by a diagonal condition: generalized Catalan numbers, Fibonacci Quart., 27 (1989) 33-46; MR 90c:05012.
[This paper contains a proof via lattice paths of the Lagrange inversion theorem for ordinary generating functions. It also includes many examples of the Catalan-Motzkin-Schröder sequence variety. A translation from lattice paths to planar trees is given along with several planar tree examples.
Basically this paper considers paths where each step is of the form
![]() ,
, ![]() . Such a path
from (0,0) to (k,l) is good if after leaving (0,0) all points
on the path must lie above the line
. Such a path
from (0,0) to (k,l) is good if after leaving (0,0) all points
on the path must lie above the line ![]() ,
, ![]() .
.
The number of good paths from (0,0) to ![]() [sic!] is shown
to be
[sic!] is shown
to be ![]() of all paths between the same points. These
paths are then weighted and generating functions are introduced,
leading, eventually, to a combinatorial proof of the Lagrange
inversion theorem.
of all paths between the same points. These
paths are then weighted and generating functions are introduced,
leading, eventually, to a combinatorial proof of the Lagrange
inversion theorem.
Other combinatorial proofs include those of Ra (ordinary generating functions), L (exponential generating functions) and G. Louis Shapiro]
Sv. Marta Sved, Math. Intelligencer
[Cf. Kl, Mi and see Gessel correspondence.]
T1. Lajos Takács, Ballot problems, Z. Wahrscheinlichkeitstheorie und verw. Gebiete, 1 (1962) 154-158; MR 26 #3131.
[The author proves a discrete variant of Spitzer's lemma, to the
effect that ![]() , where
, where
![]() is the number of positive partial sums
is the number of positive partial sums
![]() ,
, ![]() and the
and the ![]() are integer-valued
with permutation-symmetric distribution. He uses this to prove
that, if all possible voting sequences are equally likely and
the two candidates get a and b votes with (a,b) = 1, and
if
are integer-valued
with permutation-symmetric distribution. He uses this to prove
that, if all possible voting sequences are equally likely and
the two candidates get a and b votes with (a,b) = 1, and
if ![]() denotes the number of the a+b vote-count times
when the ratio of votes is
denotes the number of the a+b vote-count times
when the ratio of votes is ![]() , then
, then
![]() . The probability that the amount by
which the first candidate is ahead stays strictly between c-d and c,
where c and d are positive integers, c < d, and c-d < b-a < c, is
shown to be
. The probability that the amount by
which the first candidate is ahead stays strictly between c-d and c,
where c and d are positive integers, c < d, and c-d < b-a < c, is
shown to be
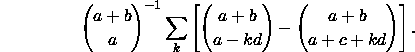
The results extend those of many authors, some of the more recent being Chung, Feller, Hodges, Gnedenko, Rvaöeva. J. Kiefer]
T2. Lajos Takács, The distribution of majority times in a ballot, Z. Wahrscheinlichkeitstheorie und verw. Gebiete, 2 (1963) 118-121; MR 28 #3490.
[In this sequel to a previous paper [T1] further probabilities are calculated concerning the number of times one candidate leads over another during the successive stages of a ballot. The combinatorial proofs are based on lemmas which are relevant also to fluctuation theory, order statistics and the theory of queues. The author also gives a generalization to processes with independent increments. F.L. Spitzer]
Ta. Lajos Takács, Some asymptotic formulas for lattice paths, J. Statist. Plann. Inference 14 (1986) 123-142; MR 87k:60082.
[The author proves asymptotic formulas for the area under lattice paths starting at (0,0) with unit steps in the positive x- and y-directions. Two of the simpler formulas are as follows.
Let ![]() be the area under a random path of length n. Then
be the area under a random path of length n. Then
![]()
uniformly in j for j=0, 1, ..., ![]() ,
where
,
where ![]() .
.
Let ![]() be the area under a random path from (0,0)
to (a,b). Then
be the area under a random path from (0,0)
to (a,b). Then
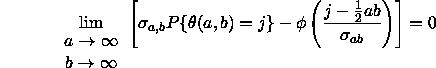
uniformly in j for ![]() ,
where
,
where ![]() is a positive real number and
is a positive real number and
![]() .
.
Let w(n,j) be the number of lattice paths from (0,0) to (n,n)
with area j which stay below the line y = x for 0 < x < n. Let ![]() be the Catalan number
be the Catalan number ![]() , and let
, and let ![]() be
the discrete random variable whose probability distribution is
given by
be
the discrete random variable whose probability distribution is
given by ![]() . The author
gives empirical evidence that suggests
. The author
gives empirical evidence that suggests
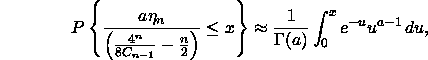
where ![]() . Ira Gessel]
. Ira Gessel]
11. H.M. Taylor & R.C. Rowe, Note on a geometrical theorem, Proc. London Math. Soc. 13 (1882) 102-106.
12. W.T. Tutte, A census of Hamiltonian polygons, Canad. J. Math., 14 (1962) 402-417; MR 25 #1108.
The number of inequivalent rooted maps of 2n vertices is
![]()
and number of inequivalent Hamiltonian rooted maps of 2n vertices is
![]()
W1. Toshihiro Watanabe & Sri Gopal Mohanty, On an inclusion-exclusion formula based on the reflection principle, Discrete Math. 64 (1987) 281-288; MR 88d:05012.
[A1 first used the refexion principle to count paths in the plane, with unit steps in the positive horizontal and vertical directions, that never touch the line x = y. Suppose that lattice points p and q lie on the same side of this line. The number of ``good paths'' from p to q is the total number of paths from p to q minus the number of ``bad paths'' from p to q (those which touch the line). By reflecting in the line x = y the segment of a bad path from its starting point to its first meeting with this line, we find that the number of bad paths from p to q is equal to the total number of paths from p' to q, where p' is the reflexion of p in x = y.
The authors show here how André's reflexion principle can be used
to solve the multidimensional generalization of the ballot
problem, which is equivalent to counting paths not touching the
hyperplanes ![]() , i, j=1, ..., n. Here all reflexions
in the hyperplanes
, i, j=1, ..., n. Here all reflexions
in the hyperplanes ![]() are used and there are n! terms in
the resulting formula, with alternating signs, corresponding to
the n! permutations of the coordinates generated by the reflexions
in the hyperplanes. A similar proof was given by Ze; the
authors' proof describes in more detail the successive reflexions
applied to a path. Ira Gessel]
are used and there are n! terms in
the resulting formula, with alternating signs, corresponding to
the n! permutations of the coordinates generated by the reflexions
in the hyperplanes. A similar proof was given by Ze; the
authors' proof describes in more detail the successive reflexions
applied to a path. Ira Gessel]
W2. Toshihiro Watanabe, On a determinant sequence in the lattice path counting, J. Math. Anal. Appl. 123 (1987) 401-414; MR 88g:05015.
[The number of lattice paths connecting two given lattice points and staying between upper and lower boundaries can be expressed by a determinant involving binomial coefficients, due to G. Kreweras. The recursive nature of this problem leads to a system of difference equations, and the same type of solution (determinants involving polynomials of binomial type) applies to a much larger class of operator equations. The author makes a new approach by associating such determinants with random tableaux. He obtains determinant sequences which satisfy a convolution identity similar to sequences of binomial type. The theory is then applied to Hill's enzyme model, reproducing a result of Shapiro and Zeilberger. Heinrich Niederhausen] [cf. K2, Hi, SZ]
W3. Toshihiro Watanabe, On a generalization of polynomials in the ballot problem, J. Statist. Plann. Inference 14 (1986) 143-152; MR 87j:05024.
[The ballot-polynomials ![]() are
Sheffer polynomials for the backwards difference operator
are
Sheffer polynomials for the backwards difference operator ![]() .
They are the solutions of the system of operator equations
.
They are the solutions of the system of operator equations
![]() , uniquely determined by the initial
conditions
, uniquely determined by the initial
conditions ![]() for all x, and
for all x, and ![]() for all
for all
![]() . Using his earlier results on multivariate umbral
calculus, the author shows how to solve the n-dimensional
system
. Using his earlier results on multivariate umbral
calculus, the author shows how to solve the n-dimensional
system ![]() for all i=1, ..., n, where
for all i=1, ..., n, where
![]() is a delta set and
is a delta set and ![]() stands for the ith unit vector. The general solution for such a
system is then specialized to give an n-dimensional version of
the ballot polynomials.
stands for the ith unit vector. The general solution for such a
system is then specialized to give an n-dimensional version of
the ballot polynomials.
A generalized version of the classical ballot problem, attributed to Takács, is solved by the polynomials
![]()
The n-dimensional analog is obtained from a very general setting, leading to a so-called ``multinomial basic polynomial sequence''. Heinrich Niederhausen]
W4. Toshihiro Watanabe, On the Littlewood-Richardson rule in terms of lattice path combinatorics, Proc. First Japan Conf. Graph Theory & Appl., Discrete Math. 72 (1988) 385-390; MR 90b:05010.
[This paper gives a proof of the Littlewood-Richardson rule for multiplying Schur functions by using the characterization of Schur functions as collections of nonintersecting lattice paths. The proof is based on Robinson's recomposition rule for transforming non-lattice paths into lattice paths. Dennis White]
Ze. Doron Zeilberger, André's reflection proof generalized to the many-candidate ballot problem, Discrete Math. 44 (1983) 325-326; MR 84g:05016.
[The n-candidate ballot problem is the problem of counting those
lattice walks from the origin to the point ![]() ,
,
![]() , which never touch any of the
hyperplanes
, which never touch any of the
hyperplanes ![]() . The problem is equivalent to that of
counting Young tableaux of a given shape. D. André [A1]
showed that for n=2 the answer is
. The problem is equivalent to that of
counting Young tableaux of a given shape. D. André [A1]
showed that for n=2 the answer is
![]() as follows:
as follows:
![]() counts all paths from (0,0) to
counts all paths from (0,0) to
![]() . If a path touches
. If a path touches ![]() , reflect the initial
segment up to the first such touch in this line to get a path
from (-1,1) to
, reflect the initial
segment up to the first such touch in this line to get a path
from (-1,1) to ![]() . This gives a bijection between
``bad'' paths from (0,0) to
. This gives a bijection between
``bad'' paths from (0,0) to ![]() and all paths from
(-1,1) to
and all paths from
(-1,1) to ![]() which proves the formula.
which proves the formula.
The author generalizes this argument to obtain the determinant
formula (due to Frobenius and MacMahon)
![]() . Here a term corresponding to
a permutation
. Here a term corresponding to
a permutation ![]() counts paths from
counts paths from
![]() to
to
![]() . The ``bad'' paths are cancelled in pairs
by reflexion in the hyperplanes
. The ``bad'' paths are cancelled in pairs
by reflexion in the hyperplanes ![]() . A related approach,
using recurrences instead of reflexion, was recently given by
N. Linial [Li]. Ira Gessel]
. A related approach,
using recurrences instead of reflexion, was recently given by
N. Linial [Li]. Ira Gessel]
The author thanks Marc Paulhus, who converted this paper from latex to html using Nikos Drake's Latex2Html translator.
(Concerned with sequences A000108, A000245, A000337, A000344, A000356, A000588, A000589, A000590, A001392, A001405, A001700, A002057, A003517, A003518, A003519, A005557, A005558, A005559, A005560, A005561, A005562, A005563, A005564, A005565, A005566, A005567, A005568, A005569, A005570, A005571, A005572, A005573, A005586, A005587, A008315, A036799, A039598, A047072, A050166, A052173, A052174, A052175, A052176, A052177, A052178, A052179 )
Received March 26, 1999; revised version received September 18, 1999. Published in Journal of Integer Sequences Jan. 27, 2000.