We first prove two results which both imply that for any sequence
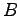
of asymptotic density zero there exists an infinite sequence
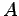
such that the sum of any number of distinct elements of
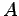
does not belong to
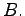
Then, for any
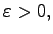
we construct an
infinite sequence of positive integers
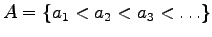
satisfying
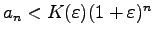
for each
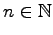
such
that no sum of some distinct elements of
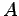
is a perfect square.
Finally, given any finite set
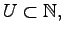
we construct a
sequence
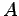
of the same growth, namely,
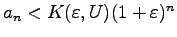
for every
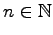
such that no sum of its distinct
elements is equal to
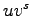
with
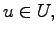
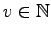
and
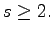
Received November 13 2006;
revised version received December 4 2006.
Published in Journal of Integer Sequences December 4 2006.

