 |
Journal of Integer Sequences, Vol. 1 (1998), Article 98.1.8 |
 |
Journal of Integer Sequences, Vol. 1 (1998), Article 98.1.8 |
Email addresses: duke@math.rutgers.edu,
greenfie@math.rutgers.edu,
speer@math.rutgers.edu
Abstract: The terms of A000278, the sequence defined by h0 = 0, h1 = 1, and hn+2 = hn+1 + hn2, count the trees in certain recursively defined forests. We show that for n large, hn is approximately Asqrt(2)n for n even and hn is approximately Bsqrt(2)n for n odd, with A,B > 1 and A not equal to B, and we give estimates of A and B: A is 1.436 ± .001 and B is 1.452 ± .001. The doubly exponential growth of the sequence is not surprising (see, for example, [AS]) but the dependence of the growth on the parity of the subscript is more interesting. Numerical and analytical investigation of similar sequences suggests a possible generalization of this result to a large class of such recursions.
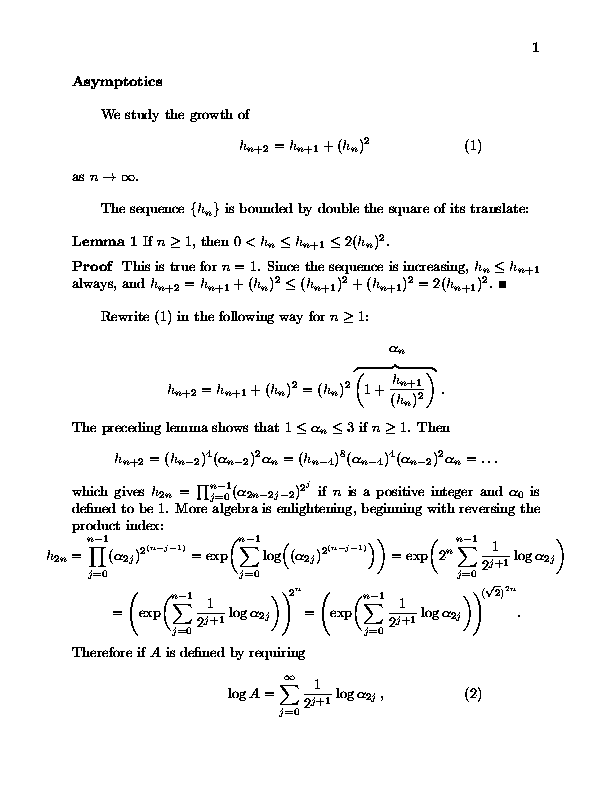








This paper was written in December 1997 with revisions written in February and May 1998, and was based primarily on work done in 1993. Published in Journal of Integer Sequences, October 30 1998.