4.6 Number of templates
To search for gravitational-wave signals we evaluate the 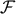 -statistic on a grid in parameter space. The
grid has to be sufficiently fine such that the loss of signals is minimized. In order to estimate the number of
points of the grid, or in other words the number of templates that we need to search for a signal, the natural
quantity to study is the expectation value of the
-statistic on a grid in parameter space. The
grid has to be sufficiently fine such that the loss of signals is minimized. In order to estimate the number of
points of the grid, or in other words the number of templates that we need to search for a signal, the natural
quantity to study is the expectation value of the 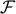 -statistic when the signal is present. We have
The components of the matrix
-statistic when the signal is present. We have
The components of the matrix 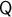 are given in Equation (52). Let us rewrite the expectation value (63) in
the following form,
where
are given in Equation (52). Let us rewrite the expectation value (63) in
the following form,
where 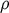 is the signal-to-noise ratio. Let us also define the normalized correlation function
From the Rayleigh principle [67] it follows that the minimum of the normalized correlation function
is equal to the smallest eigenvalue of the normalized matrix
is the signal-to-noise ratio. Let us also define the normalized correlation function
From the Rayleigh principle [67] it follows that the minimum of the normalized correlation function
is equal to the smallest eigenvalue of the normalized matrix 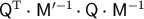 , whereas
the maximum is given by its largest eigenvalue. We define the reduced correlation function as
As the trace of a matrix equals the sum of its eigenvalues, the reduced correlation function
, whereas
the maximum is given by its largest eigenvalue. We define the reduced correlation function as
As the trace of a matrix equals the sum of its eigenvalues, the reduced correlation function
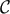 is equal to the average of the eigenvalues of the normalized correlation function
is equal to the average of the eigenvalues of the normalized correlation function 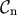 . In
this sense we can think of the reduced correlation function as an “average” of the normalized
correlation function. The advantage of the reduced correlation function is that it depends only on
the intrinsic parameters
. In
this sense we can think of the reduced correlation function as an “average” of the normalized
correlation function. The advantage of the reduced correlation function is that it depends only on
the intrinsic parameters 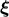 , and thus it is suitable for studying the number of grid points on
which the
, and thus it is suitable for studying the number of grid points on
which the 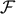 -statistic needs to be evaluated. We also note that the normalized correlation
function
-statistic needs to be evaluated. We also note that the normalized correlation
function 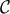 precisely coincides with the autocovariance function
precisely coincides with the autocovariance function 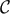 of the
of the 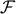 -statistic given by
Equation (51).
-statistic given by
Equation (51).
Like in the calculation of the number of cells in order to estimate the number of templates we perform a
Taylor expansion of 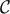 up to second order terms around the true values of the parameters, and we obtain
an equation analogous to Equation (57),
up to second order terms around the true values of the parameters, and we obtain
an equation analogous to Equation (57),
where 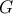 is given by Equation (56). By arguments identical to those in deriving the formula for the
number of cells we arrive at the following formula for the number of templates:
When
is given by Equation (56). By arguments identical to those in deriving the formula for the
number of cells we arrive at the following formula for the number of templates:
When 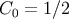 the above formula coincides with the formula for the number
the above formula coincides with the formula for the number 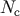 of cells,
Equation (60). Here we would like to place the templates sufficiently closely so that the loss of
signals is minimized. Thus
of cells,
Equation (60). Here we would like to place the templates sufficiently closely so that the loss of
signals is minimized. Thus 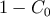 needs to be chosen sufficiently small. The formula (68) for
the number of templates assumes that the templates are placed in the centers of hyperspheres
and that the hyperspheres fill the parameter space without holes. In order to have a tiling of
the parameter space without holes we can place the templates in the centers of hypercubes
which are inscribed in the hyperspheres. Then the formula for the number of templates reads
needs to be chosen sufficiently small. The formula (68) for
the number of templates assumes that the templates are placed in the centers of hyperspheres
and that the hyperspheres fill the parameter space without holes. In order to have a tiling of
the parameter space without holes we can place the templates in the centers of hypercubes
which are inscribed in the hyperspheres. Then the formula for the number of templates reads
For the case of the signal given by Equation (16) our formula for number of templates is equivalent to
the original formula derived by Owen [74 ]. Owen [74] has also introduced a geometric approach to the
problem of template placement involving the identification of the Fisher matrix with a metric on the
parameter space. An early study of the template placement for the case of coalescing binaries can be found
in [84, 35, 19
]. Owen [74] has also introduced a geometric approach to the
problem of template placement involving the identification of the Fisher matrix with a metric on the
parameter space. An early study of the template placement for the case of coalescing binaries can be found
in [84, 35, 19 ]. Applications of the geometric approach of Owen to the case of spinning neutron stars and
supernova bursts are given in [24, 11].
]. Applications of the geometric approach of Owen to the case of spinning neutron stars and
supernova bursts are given in [24, 11].
The problem of how to cover the parameter space with the smallest possible number of templates, such
that no point in the parameter space lies further away from a grid point than a certain distance, is known in
mathematical literature as the covering problem [28]. The maximum distance of any point to the
next grid point is called the covering radius 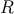 . An important class of coverings are lattice
coverings. We define a lattice in
. An important class of coverings are lattice
coverings. We define a lattice in 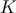 -dimensional Euclidean space
-dimensional Euclidean space 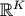 to be the set of points
including
to be the set of points
including 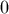 such that if
such that if 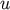 and
and 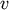 are lattice points, then also
are lattice points, then also 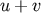 and
and 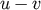 are
lattice points. The basic building block of a lattice is called the fundamental region. A lattice
covering is a covering of
are
lattice points. The basic building block of a lattice is called the fundamental region. A lattice
covering is a covering of 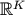 by spheres of covering radius
by spheres of covering radius 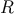 , where the centers of the
spheres form a lattice. The most important quantity of a covering is its thickness
, where the centers of the
spheres form a lattice. The most important quantity of a covering is its thickness 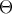 defined as
defined as
In the case of a two-dimensional Euclidean space the best covering is the hexagonal covering and its
thickness 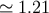 . For dimensions higher than 2 the best covering is not known. We know however the best
lattice covering for dimensions
. For dimensions higher than 2 the best covering is not known. We know however the best
lattice covering for dimensions 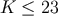 . These are so-called
. These are so-called 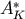 lattices which have a thickness
lattices which have a thickness 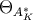 equal to
where
equal to
where 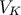 is the volume of the
is the volume of the 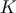 -dimensional sphere of unit radius.
-dimensional sphere of unit radius.
For the case of spinning neutron stars a 3-dimensional grid was constructed consisting of prisms with
hexagonal bases [16 ]. This grid has a thickness around 1.84 which is much better than the cubic grid which
has thickness of approximately 2.72. It is worse than the best lattice covering which has the thickness
around 1.46. The advantage of an
]. This grid has a thickness around 1.84 which is much better than the cubic grid which
has thickness of approximately 2.72. It is worse than the best lattice covering which has the thickness
around 1.46. The advantage of an 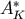 lattice over the hypercubic lattice grows exponentially with the
number of dimensions.
lattice over the hypercubic lattice grows exponentially with the
number of dimensions.
![]() up to second order terms around the true values of the parameters, and we obtain
an equation analogous to Equation (57
up to second order terms around the true values of the parameters, and we obtain
an equation analogous to Equation (57![]() ),
), ![]() ) our formula for number of templates is equivalent to
the original formula derived by Owen [74
) our formula for number of templates is equivalent to
the original formula derived by Owen [74![]() ]. Owen [74] has also introduced a geometric approach to the
problem of template placement involving the identification of the Fisher matrix with a metric on the
parameter space. An early study of the template placement for the case of coalescing binaries can be found
in [84, 35, 19
]. Owen [74] has also introduced a geometric approach to the
problem of template placement involving the identification of the Fisher matrix with a metric on the
parameter space. An early study of the template placement for the case of coalescing binaries can be found
in [84, 35, 19![]() ]. Applications of the geometric approach of Owen to the case of spinning neutron stars and
supernova bursts are given in [24, 11].
]. Applications of the geometric approach of Owen to the case of spinning neutron stars and
supernova bursts are given in [24, 11].
![]() . An important class of coverings are lattice
coverings. We define a lattice in
. An important class of coverings are lattice
coverings. We define a lattice in ![]() -dimensional Euclidean space
-dimensional Euclidean space ![]() to be the set of points
including
to be the set of points
including ![]() such that if
such that if ![]() and
and ![]() are lattice points, then also
are lattice points, then also ![]() and
and ![]() are
lattice points. The basic building block of a lattice is called the fundamental region. A lattice
covering is a covering of
are
lattice points. The basic building block of a lattice is called the fundamental region. A lattice
covering is a covering of ![]() by spheres of covering radius
by spheres of covering radius ![]() , where the centers of the
spheres form a lattice. The most important quantity of a covering is its thickness
, where the centers of the
spheres form a lattice. The most important quantity of a covering is its thickness ![]() defined as
defined as
![]() ]. This grid has a thickness around 1.84 which is much better than the cubic grid which
has thickness of approximately 2.72. It is worse than the best lattice covering which has the thickness
around 1.46. The advantage of an
]. This grid has a thickness around 1.84 which is much better than the cubic grid which
has thickness of approximately 2.72. It is worse than the best lattice covering which has the thickness
around 1.46. The advantage of an ![]() lattice over the hypercubic lattice grows exponentially with the
number of dimensions.
lattice over the hypercubic lattice grows exponentially with the
number of dimensions.