4.1 Bayesian estimation
We assign a cost function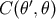 
of estimating the true value of 
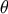as 
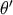. We then associate with
an estimator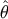 
a conditional risk or cost averaged over all realizations of data 
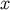for each value of the
parameter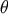 
:
where 
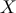is the set of observations and 
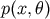is the joint probability distribution of data 
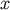and
parameter 
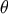. We further assume that there is a certain a priori probability distribution 
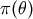of the
parameter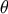 
. We then define the Bayes estimator as the estimator that minimizes the average risk defined
as
where E is the expectation value with respect to an a priori distribution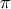 
, and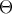 
is the set of
observations of the parameter 
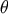. It is not difficult to show that for a commonly used cost function
the Bayesian estimator is the conditional mean of the parameter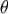 
given data 
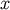, i.e.,
Update
where 
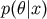is the conditional probability density of parameter 
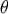given the data
.
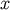![∫ ( ) R (ˆθ) = E [C (ˆθ,θ)] = C ˆθ(x ),θ p(x, θ)dx, (25 ) θ θ X](article167x.gif){kind=small}
![∫ ∫ ( ) ˆ ˆ ˆ r(θ) = E[Rθ(θ)] = X Θ C θ(x ),θ p (x, θ)π(θ)dθ dx, (26 )](article174x.gif){kind=small}
![∫ ˆ θ(x) = E [θ|x ] = Θ θp(θ|x) dθ, (28 )](article181x.gif){kind=small}