4.2 Maximum a posteriori probability estimation
Suppose that in a given estimation problem we are not able to assign a particular cost function
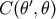 . Then a natural choice is a uniform cost function equal to
. Then a natural choice is a uniform cost function equal to 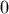 over a certain interval
over a certain interval 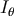 of the
parameter
of the
parameter 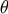 . From Bayes theorem [20] we have
where
. From Bayes theorem [20] we have
where 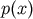 is the probability distribution of data
is the probability distribution of data 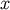 . Then from Equation (26) one can deduce that for
each data
. Then from Equation (26) one can deduce that for
each data 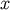 the Bayes estimate is any value of
the Bayes estimate is any value of 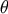 that maximizes the conditional probability
that maximizes the conditional probability 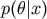 .
The density
.
The density 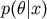 is also called the a posteriori probability density of parameter
is also called the a posteriori probability density of parameter 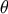 and the
estimator that maximizes
and the
estimator that maximizes 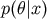 is called the maximum a posteriori (MAP) estimator. It is
denoted by
is called the maximum a posteriori (MAP) estimator. It is
denoted by 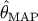 . We find that the MAP estimators are solutions of the following equation
which is called the MAP equation.
. We find that the MAP estimators are solutions of the following equation
which is called the MAP equation.