[1]    Adamczak, R. (2011). On the Marchenko-Pastur and circular laws for some classes of random matrices with dependent entries. Electronic Journal of Probability 16 1065–1095.

[2]    Akemann, G. and Kanzieper, E. (2007). Integrable structure of Ginibre’s ensemble of real random matrices and a Pfaffian integration theorem. J. Stat. Phys. 129 1159–1231. 10.1007/s10955-007-9381-2 MR2363393 (2009a:82024)

[3]    Akemann, G., Phillips, M. J. and Shifrin, L. (2009). Gap probabilities in non-Hermitian random matrix theory. J. Math. Phys. 50 063504, 32. 10.1063/1.3133108 MR2536111 (2010f:60017)

[4]    Aldous, D. (1992). Asymptotics in the random assignment problem. Probab. Theory Related Fields 93 507–534.

[5]    Aldous, D. and Lyons, R. (2007). Processes on unimodular random networks. Electron. J. Probab. 12 no. 54, 1454–1508 (electronic).

[6]    Aldous, D. and Steele, J. M. (2004). The objective method: probabilistic combinatorial optimization and local weak convergence. In Probability on discrete structures. Encyclopaedia Math. Sci. 110 1–72. Springer, Berlin.

[7]    Anderson, G. W., Guionnet, A. and Zeitouni, O. (2010). An introduction to random matrices. Cambridge Studies in Advanced Mathematics 118. Cambridge University Press, Cambridge. MR2760897

[8]    Andrew, A. L. (1990). Eigenvalues and singular values of certain random matrices. J. Comput. Appl. Math. 30 165–171.

[9]    Azaïs, J.-M. and Wschebor, M. (2005). On the roots of a random system of equations. The theorem on Shub and Smale and some extensions. Found. Comput. Math. 5 125–144. 10.1007/s10208-004-0119-0 MR2149413 (2006h:60087)

[10]    Bai, Z. D. (1997). Circular law. Ann. Probab. 25 494–529.

[11]    Bai, Z. D. and Silverstein, J. W. (2006). Spectral Analysis of Large Dimensional Random Matrices. Mathematics Monograph Series 2. Science Press, Beijing.

[12]    Bai, Z. D., Silverstein, J. W. and Yin, Y. Q. (1988). A note on the largest eigenvalue of a large-dimensional sample covariance matrix. J. Multivariate Anal. 26 166–168.

[13]    Bai, Z. D. and Yin, Y. Q. (1986). Limiting behavior of the norm of products of random matrices and two problems of Geman-Hwang. Probab. Theory Related Fields 73 555–569.

[14]    Bai, Z. D. and Yin, Y. Q. (1993). Limit of the smallest eigenvalue of a large-dimensional sample covariance matrix. Ann. Probab. 21 1275–1294.

[15]    Belinschi, S., Dembo, A. and Guionnet, A. (2009). Spectral measure of heavy tailed band and covariance random matrices. Comm. Math. Phys. 289 1023–1055.

[16]    Ben Arous, G. and Guionnet, A. (2008). The spectrum of heavy tailed random matrices. Comm. Math. Phys. 278 715–751.

[17]    Ben Arous, G. and Zeitouni, O. (1998). Large deviations from the circular law. ESAIM Probab. Statist. 2 123–134 (electronic). 10.1051/ps:1998104 MR1660943 (2000g:60045)

[18]    Benaych-Georges, F. and Chapon, F. (2011). Random right eigenvalues of Gaussian quaternionic matrices. preprint arXiv:1104.4455 [math.PR].

[19]    Bender, M. (2010). Edge scaling limits for a family of non-Hermitian random matrix ensembles. Probab. Theory Related Fields 147 241–271.

[20]    Biane, P. and Lehner, F. (2001). Computation of some examples of Brown’s spectral measure in free probability. Colloq. Math. 90 181–211.

[21]    Bloom, T. and Shiffman, B. (2007). Zeros of random polynomials on ℂ ^m. Math. Res. Lett. 14 469–479. MR2318650 (2008f:32009)

[22]    Bordenave, C. (2011). On the spectrum of sum and product of non-Hermitian random matrices. Electronic Communications in Probability 16 104–113.

[23]    Bordenave, C., Caputo, P. and Chafaï, D. (2011). Circular Law Theorem for Random Markov Matrices. preprint arXiv:0808.1502 [math.PR] to appear in Probab. Theor. and Related Fields.

[24]    Bordenave, C., Caputo, P. and Chafaï, D. (2011). The spectral measure of random generators. preprint in preparation.

[25]    Bordenave, C., Caputo, P. and Chafaï, D. (2011). Spectrum of large random reversible Markov chains: Heavy-tailed weigths on the complete graph. Annals of Probability 39 1544–1590.

[26]    Bordenave, C., Caputo, P. and Chafaï, D. (2011). Spectrum of non-Hermitian heavy tailed random matrices. Communications in Mathematical Physics 307 513–560.

[27]    Borodin, A. and Sinclair, C. D. (2009). The Ginibre ensemble of real random matrices and its scaling limits. Comm. Math. Phys. 291 177–224. 10.1007/s00220-009-0874-5 MR2530159 (2010e:60012)

[28]    Bouchaud, J. P. and Cizeau, P. (1994). Theory of Lévy matrices. Phys. Rev. E 3 1810–1822.

[29]    Bourgain, J., Vu, V. H. and Wood, P. M. (2010). On the singularity probability of discrete random matrices. J. Funct. Anal. 258 559–603. 10.1016/j.jfa.2009.04.016 MR2557947

[30]    Brown, L. G. (1986). Lidskiĭ’s theorem in the type II case. In Geometric methods in operator algebras (Kyoto, 1983). Pitman Res. Notes Math. Ser. 123 1–35. Longman Sci. Tech., Harlow.

[31]    Chafaï, D. (2010). Circular law for noncentral random matrices. Journal of Theoretical Probability 23 945–950.

[32]    Chafaï, D. (2010). The Dirichlet Markov Ensemble. J. of Multivariate Analysis 101 555–567.

[33]    Chafaï, D., Guédon, O., Lecué, G. and Pajor, A. (2011). Interactions between compressed sensing, random matrices, and high dimensional geometry. forthcoming book [URL].

[34]    Chatterjee, S. (2006). A generalization of the Lindeberg principle. Ann. Probab. 34 2061–2076.

[35]    Chatterjee, S., Diaconis, P. and Sly, A. (2010). Properties of Uniform Doubly Stochastic Matrices. preprint arXiv:1010.6136 [math.PR].

[36]    Chen, Z., Zhang, J.-T. and Hu, F., eds. (2008). Advances in statistics. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ Including the proceedings of the conference in honor of Professor Zhidong Bai on his 65th birthday, held at the National Uni. of Singapore, Singapore, July 20, 2008. MR2407790 (2009f:62003)

[37]    Dellacherie, C. and Meyer, P.-A. (1978). Probabilities and potential. North-Holland Mathematics Studies 29. North-Holland Publishing Co., Amsterdam.

[38]    Dong, Z., Jiang, T. and Li, D. (2011). Circular Law and Arc Law for Truncation of Random Unitary Matrix. preprint, personal communication by Tiefeng Jiang.

[39]    Dozier, R. B. and Silverstein, J. W. (2007). On the empirical distribution of eigenvalues of large dimensional information-plus-noise-type matrices. J. Multiv. Anal. 98 678–694.

[40]    Edelman, A. (1988). Eigenvalues and condition numbers of random matrices. SIAM J. Matrix Anal. Appl. 9 543–560.

[41]    Edelman, A. (1997). The probability that a random real Gaussian matrix has k real eigenvalues, related distributions, and the circular law. J. Multivariate Anal. 60 203–232.

[42]    Edelman, A. and Kostlan, E. (1995). How many zeros of a random polynomial are real? Bull. Amer. Math. Soc. (N.S.) 32 1–37. 10.1090/S0273-0979-1995-00571-9 MR1290398 (95m:60082)

[43]    Edelman, A. and Kostlan, E. (1996). Erratum: “How many zeros of a random polynomial are real?” [Bull. Amer. Math. Soc. (N.S.) 32 (1995), no. 1, 1–37]. Bull. Amer. Math. Soc. (N.S.) 33 325. 10.1090/S0273-0979-96-00678-7 MR1376652

[44]    Edelman, A., Kostlan, E. and Shub, M. (1994). How many eigenvalues of a random matrix are real? J. Amer. Math. Soc. 7 247–267.

[45]    Emiris, I., Galligo, A. and Tsigaridas, E. (2010). Random polynomials and expected complexity of bisection methods for real solving. preprint arXiv:1005.2001 [cs.SC].

[46]    Erd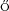s, L., Schlein, B. and Yau, H.-T. (2010). Wegner estimate and level repulsion for Wigner random matrices. Int. Math. Res. Not. IMRN 3 436–479.

[47]    Feinberg, J. and Zee, A. (1997). Non-Gaussian non-Hermitian random matrix theory: phase transition and addition formalism. Nuclear Phys. B 501 643–669.

[48]    Feinberg, J. and Zee, A. (1997). Non-Hermitian Random Matrix Theory: Method of Hermitian Reduction. Nucl. Phys. B 3 579–608.

[49]    Forrester, P. J. (2010). Log-gases and random matrices. London Mathematical Society Monographs Series 34. Princeton University Press, Princeton, NJ. MR2641363

[50]    Forrester, P. J. and Krishnapur, M. (2009). Derivation of an eigenvalue probability density function relating to the Poincaré disk. J. of Physics A: Math. and Theor. 42 385204.

[51]    Fuglede, B. and Kadison, R. V. (1952). Determinant theory in finite factors. Ann. of Math. (2) 55 520–530.

[52]    Galligo, A. (2010). Intriguing Patterns in the Roots of the Derivatives of some Random Polynomials. preprint oai:hal.inria.fr:i nria-00552081.

[53]    Ginibre, J. (1965). Statistical ensembles of complex, quaternion, and real matrices. J. Mathematical Phys. 6 440–449.

[54]    Girko, V. L. (1984). The circular law. Teor. Veroyatnost. i Primenen. 29 669–679.

[55]    Girko, V. L. (1990). Theory of random determinants. Mathematics and its Applications (Soviet Series) 45. Kluwer Academic Publishers Group, Dordrecht. Translated from the Russian.

[56]    Girko, V. L. (1994). The circular law: ten years later. Random Oper. Stochastic Equations 2 235–276.

[57]    Girko, V. L. (2001). Theory of stochastic canonical equations. Vol. I. Mathematics and its Applications 535. Kluwer Academic Publishers, Dordrecht. MR1887675 (2003f:60048)

[58]    Girko, V. L. (2004). The strong circular law. Twenty years later. I. Random Oper. Stochastic Equations 12 49–104.

[59]    Girko, V. L. (2004). The strong circular law. Twenty years later. II. Random Oper. Stochastic Equations 12 255–312.

[60]    Girko, V. L. (2005). The circular law. Twenty years later. III. Random Oper. Stochastic Equations 13 53–109.

[61]    Girko, V. L. and Vladimirova, A. I. (2010). L.I.F.E.: ∏ _j=1^mH_n^(j) ∼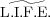 ∼{H_n⁽¹⁾}^m and Halloween Law. Random Oper. Stoch. Equ. 18 327–353. 10.1515/ROSE.2010.018 MR2747827

[62]    Goldman, A. (2010). The Palm measure and the Voronoi tessellation for the Ginibre process. Ann. Appl. Probab. 20 90–128. 10.1214/09-AAP620 MR2582643 (2011d:60038)

[63]    Goldsheid, I. Y. and Khoruzhenko, B. A. (2000). Eigenvalue curves of asymmetric tridiagonal random matrices. Electron. J. Probab. 5 no. 16, 28 pp. (electronic). MR1800072 (2002j:82061)

[64]    Goldsheid, I. Y. and Khoruzhenko, B. A. (2005). The Thouless formula for random non-Hermitian Jacobi matrices. Israel J. Math. 148 331–346. Probability in mathematics. 10.1007/BF02775442 MR2191234 (2006k:47082)

[65]    Golub, G. H. and Van Loan, C. F. (1996). Matrix computations, third ed. Johns Hopkins Studies in the Mathematical Sciences. Johns Hopkins University Press, Baltimore, MD.

[66]    Götze, F. and Tikhomirov, A. (2010). The circular law for random matrices. Ann. Probab. 38 1444–1491. 10.1214/09-AOP522 MR2663633

[67]    Götze, F. and Tikhomirov, A. (2010). On the Asymptotic Spectrum of Products of Independent Random Matrices. arXiv:1012.2710 [math.PR].

[68]    Götze, F. and Zaporozhets, D. (2011). On the Distribution of Complex Roots of Random Polynomials with Heavy-tailed Coefficients. arXiv:1104.5360 [math.PR].

[69]    Gudowska-Nowak, E., Jarosz, A., Nowak, M. and Pappe, G. (2007). Towards non-Hermitian random Lévy matrices. Acta Physica Polonica B 38 4089–4104.

[70]    Guionnet, A., Krishnapur, M. and Zeitouni, O. (2009). The single ring theorem. preprint available on arXiv:0909.2214 [math.PR] to appear in the Annals of Mathematics.

[71]    Guionnet, A., Wood, P. M. and Zeitouni, O. (2011). Convergence of the spectral measure of non normal matrices. preprint arXiv:1110.2471 [math.PR].

[72]    Guionnet, A. and Zeitouni, O. (2000). Concentration of the spectral measure for large matrices. Electron. Comm. Probab. 5 119–136 (electronic).

[73]    Guionnet, A. and Zeitouni, O. (2010). Support convergence in the single ring theorem. preprint arXiv:1012.2624 [math.PR].

[74]    Guntuboyina, A. and Leeb, H. (2009). Concentration of the spectral measure of large Wishart matrices with dependent entries. Electron. Commun. Probab. 14 334–342. MR2535081 (2011c:60023)

[75]    Haagerup, U. and Larsen, F. (2000). Brown’s spectral distribution measure for R-diagonal elements in finite von Neumann algebras. J. Funct. Anal. 176 331–367.

[76]    Haagerup, U. and Schultz, H. (2007). Brown measures of unbounded operators affiliated with a finite von Neumann algebra. Math. Scand. 100 209–263. MR2339369 (2008m:46139)

[77]    Hammersley, J. M. (1956). The zeros of a random polynomial. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, 1954–1955, vol. II 89–111. University of California Press, Berkeley and Los Angeles. MR0084888 (18,941c)

[78]    Holz, D. E., Orland, H. and Zee, A. (2003). On the remarkable spectrum of a non-Hermitian random matrix model. J. Phys. A 36 3385–3400. Random matrix theory. 10.1088/0305-4470/36/12/330 MR1986425 (2004e:82033)

[79]    Hörmander, L. (1983). The analysis of linear partial differential operators. I. Fundamental Principles of Mathematical Sciences 256. Springer-Verlag Distribution theory and Fourier analysis. MR717035 (85g:35002a)

[80]    Horn, A. (1954). On the eigenvalues of a matrix with prescribed singular values. Proc. Amer. Math. Soc. 5 4–7. MR0061573 (15,847d)

[81]    Horn, R. A. and Johnson, C. R. (1990). Matrix analysis. Cambridge University Press, Cambridge. Corrected reprint of the 1985 original.

[82]    Horn, R. A. and Johnson, C. R. (1994). Topics in matrix analysis. Cambridge University Press, Cambridge. Corrected reprint of the 1991 original.

[83]    Hough, J. B., Krishnapur, M., Peres, Y. and Virág, B. (2009). Zeros of Gaussian analytic functions and determinantal point processes. University Lecture Series 51. AMS, Providence, RI. MR2552864 (2011f:60090)

[84]    Hwang, C. R. (1986). A brief survey on the spectral radius and the spectral distribution of large random matrices with i.i.d. entries. In Random matrices and their applications (Brunswick, Maine, 1984). Contemp. Math. 50 145–152. Amer. Math. Soc., Providence, RI.

[85]    Ibragimov, I. A. and Maslova, N. B. (1968). The average number of zeros of random polynomials. Vestnik Leningrad. Univ. 23 171–172. MR0238376 (38 ##6652)

[86]    Ibragimov, I. A. and Maslova, N. B. (1971). The average number of real roots of random polynomials. Dokl. Akad. Nauk SSSR 199 13–16. MR0292134 (45 ##1221)

[87]    Ibragimov, I. A. and Maslova, N. B. (1971). The mean number of real zeros of random polynomials. I. Coefficients with zero mean. Teor. Verojatnost. i Primenen. 16 229–248. MR0286157 (44 ##3371)

[88]    Ibragimov, I. A. and Maslova, N. B. (1971). The mean number of real zeros of random polynomials. II. Coefficients with a nonzero mean. Teor. Verojatnost. i Primenen. 16 495–503. MR0288824 (44 ##6019)

[89]    Jiang, T. (2009). Approximation of Haar distributed matrices and limiting distributions of eigenvalues of Jacobi ensembles. Probab. Theory Related Fields 144 221–246. 10.1007/s00440-008-0146-x MR2480790 (2010a:15080)

[90]    Johansson, K. (2007). From Gumbel to Tracy-Widom. Probab. Theory Related Fields 138 75–112. 10.1007/s00440-006-0012-7 MR2288065 (2008h:60203)

[91]    Kac, M. (1943). A correction to “On the average number of real roots of a random algebraic equation.”. Bull. Amer. Math. Soc. 49 938. MR0009655 (5,179g)

[92]    Kac, M. (1943). On the average number of real roots of a random algebraic equation. Bull. Amer. Math. Soc. 49 314–320. MR0007812 (4,196d)

[93]    Kac, M. (1949). On the average number of real roots of a random algebraic equation. II. Proc. London Math. Soc. (2) 50 390–408. MR0030713 (11,40e)

[94]    Kesten, H. (1959). Symmetric random walks on groups. Trans. Amer. Math. Soc. 92 336–354.

[95]    Khorunzhy, A., Khoruzhenko, B., Pastur, L. and Shcherbina, M. (1992). The large-n limit in statistical mechanics and the spectral theory of disordered systems. In: Phase transition and critical phenomena 15 74–239.

[96]    Kostlan, E. (1992). On the spectra of Gaussian matrices. Linear Algebra Appl. 162/164 385–388. Directions in matrix theory (Auburn, AL, 1990).

[97]    Lebœuf, P. (1999). Random analytic chaotic eigenstates. J. Statist. Phys. 95 651–664. 10.1023/A:1004595310043 MR1700934 (2000c:81077)

[98]    Ledoux, M. (2001). The concentration of measure phenomenon. Mathematical Surveys and Monographs 89. American Mathematical Society, Providence, RI. MR1849347 (2003k:28019)

[99]    Ledoux, M. (2008). Complex Hermite polynomials: from the semi-circular law to the circular law. Commun. Stoch. Anal. 2 27–32. MR2446909

[100]    LePage, R., Woodroofe, M. and Zinn, J. (1981). Convergence to a stable distribution via order statistics. Ann. Probab. 9 624–632.

[101]    Littlewood, J. E. and Offord, A. C. (1943). On the number of real roots of a random algebraic equation. III. Rec. Math. [Mat. Sbornik] N.S. 12(54) 277–286. MR0009656 (5,179h)

[102]    Litvak, A. E., Pajor, A., Rudelson, M. and Tomczak-Jaegermann, N. (2005). Smallest singular value of random matrices and geometry of random polytopes. Adv. Math. 195 491–523.

[103]    Logan, B. F. and Shepp, L. A. (1968). Real zeros of random polynomials. Proc. London Math. Soc. (3) 18 29–35. MR0234512 (38 ##2829)

[104]    Logan, B. F. and Shepp, L. A. (1968). Real zeros of random polynomials. II. Proc. London Math. Soc. (3) 18 308–314. MR0234513 (38 ##2830)

[105]    Lyons, R. (2010). Identities and inequalities for tree entropy. Combin. Probab. Comput. 19 303–313.

[106]    Male, C. (2011). Free probability on traffics: the limiting distribution of heavy Wigner and deterministic matrices. preprint, personal communication.

[107]    Maslova, N. B. (1974). The distribution of the number of real roots of random polynomials. Teor. Verojatnost. i Primenen. 19 488–500. MR0368136 (51 ##4378)

[108]    Maslova, N. B. (1974). The variance of the number of real roots of random polynomials. Teor. Verojatnost. i Primenen. 19 36–51. MR0334327 (48 ##12646)

[109]    McDiarmid, C. (1989). On the method of bounded differences. In Surveys in combinatorics, 1989 (Norwich, 1989). London Math. Soc. Lecture Note Ser. 141 148–188. CUP, Cambridge. MR1036755 (91e:05077)

[110]    McKay, B. D. (1981). The expected eigenvalue distribution of a large regular graph. Linear Algebra Appl. 40 203–216.

[111]    Meckes, M. (2009). Some results on random circulant matrices. High Dimensional Probability V: The Luminy Volume 213–223.

[112]    Mehta, M. L. (1967). Random matrices and the statistical theory of energy levels. Acad. Press.

[113]    Mehta, M. L. (2004). Random matrices, third ed. Pure and Applied Mathematics 142. Acad. Press.

[114]    O’Rourke, S. and Soshnikov, A. (2010). Products of Independent Non-Hermitian Random Matrices. preprint arXiv:1012.4497 [math.PR].

[115]    Pan, G. M. and Zhou, W. (2010). Circular law, extreme singular values and potential theory. J. Multivar. Anal. 101 645–656. http://dx.doi.org/10.1016/j.jmva.2009.08.005

[116]    Panchenko, D. and Talagrand, M. (2007). On one property of Derrida-Ruelle cascades. C. R. Math. Acad. Sci. Paris 345 653–656. 10.1016/j.crma.2007.10.035 MR2371485 (2009e:60109)

[117]    Peres, Y. and Virág, B. (2005). Zeros of the i.i.d. Gaussian power series: a conformally invariant determinantal process. Acta Math. 194 1–35. 10.1007/BF02392515 MR2231337 (2007m:60150)

[118]    Petz, D. and Hiai, F. (1998). Logarithmic energy as an entropy functional. In Advances in differential equations and mathematical physics (Atlanta, GA, 1997). Contemp. Math. 217 205–221. Amer. Math. Soc., Providence, RI. MR1606719 (99b:46101)

[119]    Popescu, I. (2009). General tridiagonal random matrix models, limiting distributions and fluctuations. Probab. Theory Related Fields 144 179–220. MR2480789

[120]    Reed, M. and Simon, B. (1980). Methods of modern mathematical physics. I, Second ed. Academic Press Inc. [Harcourt Brace Jovanovich Publishers], New York. Functional analysis.

[121]    Rider, B. (2003). A limit theorem at the edge of a non-Hermitian random matrix ensemble. J. Phys. A 36 3401–3409. Random matrix theory.

[122]    Rider, B. (2004). Deviations from the circular law. Probab. Theory Related Fields 130 337–367. 10.1007/s00440-004-0355-x MR2095933 (2005k:82023)

[123]    Rider, B. and Silverstein, J. W. (2006). Gaussian fluctuations for non-Hermitian random matrix ensembles. Ann. Probab. 34 2118–2143. 10.1214/009117906000000403 MR2294978 (2008d:60036)

[124]    Rider, B. and Virág, B. (2007). The noise in the circular law and the Gaussian free field. Int. Math. Res. Not. IMRN 2 Art. ID rnm006, 33.

[125]    Rogers, T. (2010). Universal sum and product rules for random matrices. J. Math. Phys. 51 093304, 15.

[126]    Rogers, T. and Castillo, I. P. (2009). Cavity approach to the spectral density of non-Hermitian sparse matrices. Phys. Rev. E 79 012101.

[127]    Rudelson, M. and Vershynin, R. (2008). The Littlewood-Offord problem and invertibility of random matrices. Adv. Math. 218 600–633.

[128]    Ryan, Ø. (1998). On the limit distributions of random matrices with independent or free entries. Comm. Math. Phys. 193 595–626.

[129]    Saff, E. B. and Totik, V. (1997). Logarithmic potentials with external fields. Fundamental Principles of Mathematical Sciences 316. Springer-Verlag Appendix B by Thomas Bloom. MR1485778 (99h:31001)

[130]    Schehr, G. and Majumdar, S. N. (2008). Real roots of random polynomials and zero crossing properties of diffusion equation. J. Stat. Phys. 132 235–273. 10.1007/s10955-008-9574-3 MR2415102 (2010a:81078)

[131]    Shepp, L. and Farahmand, K. (2010). Expected number of real zeros of a random polynomial with independent identically distributed symmetric long-tailed coefficients. Teor. Veroyatn. Primen. 55 196–204. 10.1137/S0040585X97984735 MR2768528

[132]    Shepp, L. A. and Vanderbei, R. J. (1995). The complex zeros of random polynomials. Trans. Amer. Math. Soc. 347 4365–4384. 10.2307/2155041 MR1308023 (96a:30006)

[133]    Shiffman, B. and Zelditch, S. (2003). Equilibrium distribution of zeros of random polynomials. Int. Math. Res. Not. 1 25–49. 10.1155/S1073792803206073 MR1935565 (2003h:60075)

[134]    Shparo, D. I. and Shur, M. G. (1962). On the distribution of roots of random polynomials. Vestnik Moskov. Univ. Ser. I Mat. Meh. 1962 40–43. MR0139199 (25 ##2635)

[135]    Shub, M. and Smale, S. (1993). Complexity of Bezout’s theorem. II. Volumes and probabilities. In Computational algebraic geometry (Nice, 1992). Progr. Math. 109 267–285. Birkhäuser. MR1230872 (94m:68086)

[136]    Silverstein, J. W. (1994). The spectral radii and norms of large-dimensional non-central random matrices. Comm. Statist. Stochastic Models 10 525–532.

[137]    Śniady, P. (2002). Random regularization of Brown spectral measure. J. Funct. Anal. 193 291–313.

[138]    Spielman, D. A. and Teng, S.-H. (2002). Smoothed analysis of algorithms. In Proceedings of the International Congress of Mathematicians, Vol. I (Beijing, 2002) 597–606. Higher Ed. Press. MR1989210 (2004d:90138)

[139]    Spielman, D. A. and Teng, S.-H. (2003). Smoothed analysis: motivation and discrete models. In Algorithms and data structures. Lecture Notes in Comput. Sci. 2748 256–270. Springer, Berlin. MR2078601 (2005c:68304)

[140]    Stieltjes, T. J. (1894). Recherches sur les fractions continues. Ann. Fac. Sci. Toulouse Sci. Math. Sci. Phys. 8 J1–J122.

[141]    Talagrand, M. (1995). Concentration of measure and isoperimetric inequalities in product spaces. Inst. Hautes Études Sci. Publ. Math. 81 73–205. MR1361756 (97h:60016)

[142]    Tao, T. (2011). Outliers in the spectrum of iid matrices with bounded rank perturbations. preprint arXiv:1012.4818 [math.PR] to appear in Probability Theory and Related Fields.

[143]    Tao, T. (2011). Topics in random matrix theory. forthcoming book [ URL].

[144]    Tao, T. and Vu, V. (2008). Random matrices: A general approach for the least singular value problem. preprint arXiv:0805.3167 [math.PR].

[145]    Tao, T. and Vu, V. (2008). Random matrices: the circular law. Commun. Contemp. Math. 10 261–307.

[146]    Tao, T. and Vu, V. (2009). From the Littlewood-Offord problem to the circular law: universality of the spectral distribution of random matrices. Bull. Amer. Math. Soc. (N.S.) 46 377–396. 10.1090/S0273-0979-09-01252-X MR2507275 (2010b:15047)

[147]    Tao, T. and Vu, V. (2009). Inverse Littlewood-Offord theorems and the condition number of random discrete matrices. Ann. of Math. (2) 169 595–632. 10.4007/annals.2009.169.595 MR2480613

[148]    Tao, T. and Vu, V. (2010). Random matrices: the distribution of the smallest singular values. Geom. Funct. Anal. 20 260–297. 10.1007/s00039-010-0057-8 MR2647142

[149]    Tao, T. and Vu, V. (2010). Random matrices: universality of ESDs and the circular law. Ann. Probab. 38 2023–2065. With an appendix by Manjunath Krishnapur. 10.1214/10-AOP534 MR2722794

[150]    Trefethen, L. N. and Embree, M. (2005). Spectra and pseudospectra. Princeton University Press, Princeton, NJ. The behavior of nonnormal matrices and operators.

[151]    Voiculescu, D. (1994). The analogues of entropy and of Fisher’s information measure in free probability theory. II. Invent. Math. 118 411–440. 10.1007/BF01231539 MR1296352 (96a:46117)

[152]    Voiculescu, D. V., Dykema, K. J. and Nica, A. (1992). Free random variables. CRM Monograph Series 1. AMS A noncommutative probability approach to free products with applications to random matrices, operator algebras and harmonic analysis on free groups.

[153]    Weyl, H. (1949). Inequalities between the two kinds of eigenvalues of a linear transformation. Proc. Nat. Acad. Sci. U. S. A. 35 408–411.

[154]    Widom, H. (1994). Eigenvalue distribution for nonselfadjoint Toeplitz matrices. In Toeplitz operators and related topics (Santa Cruz, CA, 1992). Oper. Theory Adv. Appl. 71 1–8. Birkhäuser. MR1300209 (95g:47043)

[155]    Wood, P. M. (2011). Universality and the circular law for sparse random matrices. preprint arXiv:1010.1726 [math.PR] to appear in the Annals of Applied Probability.

[156]    Zeitouni, O. and Zelditch, S. (2010). Large deviations of empirical measures of zeros of random polynomials. Int. Math. Res. Not. IMRN 20 3935–3992. MR2738347 (2011k:32029)

[157]    Zhan, X. (2002). Matrix inequalities. Lecture Notes in Mathematics 1790. Springer-Verlag.