: この文書について...
Date: 2002. 4. 24.
|
4次元スピン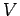 多様体上のディラック作用素の指数の評価と 多様体上のディラック作用素の指数の評価と |
| 低次元トポロジーへの応用 |
|
|
|
|
|
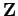 上の2次形式の中でどのようなものが4次元スピン閉多様体の交叉形式に
なりうるかについてはSeiberg-Witten理論に基づく古田氏の”10/8"定理を
始め深い結果がある。この定理は4次元スピン閉
上の2次形式の中でどのようなものが4次元スピン閉多様体の交叉形式に
なりうるかについてはSeiberg-Witten理論に基づく古田氏の”10/8"定理を
始め深い結果がある。この定理は4次元スピン閉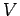 多様体
多様体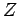 に対しても成り立つ
ことが知られており、
に対しても成り立つ
ことが知られており、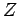 上のディラック作用素
上のディラック作用素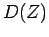 の指数
の指数
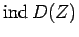 に関する
不等式として与えられる。
に関する
不等式として与えられる。
一方3次元多様体とその上のスピン構造の対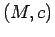 に対して
に対して
となる4次元スピン多様体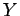 (とその上のスピン構造
(とその上のスピン構造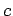 )が存在するが、
これに対して
)が存在するが、
これに対して
どのような2次形式が
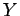
の交叉形式になりうるか

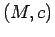 を境界とするスピン
を境界とするスピン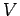 多様体
多様体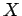 が与えられるならば
が与えられるならば
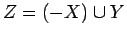 に上記の定理を適用して
に上記の定理を適用して
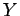 の符号数
の符号数
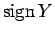 を評価することが考えられる(なるべく
ベッチ数の小さい
を評価することが考えられる(なるべく
ベッチ数の小さい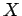 をとる方が評価は良くなる。これが
をとる方が評価は良くなる。これが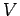 多様体を考慮に入れる
理由でもある)。ただしそのためには
多様体を考慮に入れる
理由でもある)。ただしそのためには
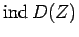 と
と
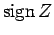 (および
(および
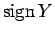 )
の差を決定しなければならない。
)
の差を決定しなければならない。
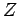 の特異点が
孤立特異点のみからなる場合にはこの差は
の特異点が
孤立特異点のみからなる場合にはこの差は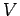 指数定理により
指数定理により
の形で与えられる。ただし右辺の和は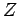 の特異点
の特異点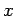 からのある寄与
からのある寄与
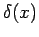 (
(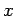 の近傍上の局所的データで決まる量)の和である。
各
の近傍上の局所的データで決まる量)の和である。
各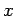 の近傍は3次元球面型多様体
の近傍は3次元球面型多様体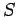 上の錐
上の錐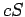 であり、
であり、
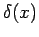 は
は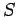 とその上のスピン構造
とその上のスピン構造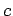 を与えると一意的に定まる(そこで
これを
を与えると一意的に定まる(そこで
これを
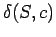 と書く)。この
と書く)。この
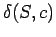 を完全に決定し、上記の問題への応用を
与えるのが今回の話のテーマである。
を完全に決定し、上記の問題への応用を
与えるのが今回の話のテーマである。
3次元多様体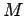 が球面型多様体
が球面型多様体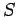 そのものである場合は上記の
そのものである場合は上記の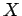 として
として
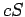 をとれる。これにより
3次元球面型多様体とそのスピン構造の対
をとれる。これにより
3次元球面型多様体とそのスピン構造の対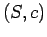 を境界とする4次元スピン多様体
を境界とする4次元スピン多様体
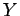 に対し
に対し
となる。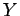 に
に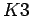 曲面(またはその向きを逆にしたもの)を連結和で加えると
曲面(またはその向きを逆にしたもの)を連結和で加えると
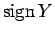 は
任意の16の倍数だけずらせるので一般にはこれ以上のことは言い得ない。しかし
は
任意の16の倍数だけずらせるので一般にはこれ以上のことは言い得ない。しかし
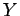 の交叉形式を定値なものに限ると10/8定理の
の交叉形式を定値なものに限ると10/8定理の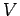 多様体版によって
結果は強まる.
多様体版によって
結果は強まる.
-
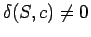 ならば
ならば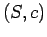 の連結和は
の連結和は
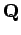 acyclicスピン多様体の境界にならない.
特に
acyclicスピン多様体の境界にならない.
特に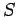 が
が
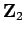 ホモロジー3球面のときは
ホモロジーコボルディズム群
ホモロジー3球面のときは
ホモロジーコボルディズム群
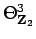 の中で無限位数.
の中で無限位数.
-
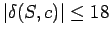 かつ
かつ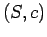 が定値スピン多様体
が定値スピン多様体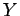 の境界ならば
の境界ならば
多くの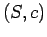 の例がこれらの条件をみたす.ただし,
の例がこれらの条件をみたす.ただし,
-
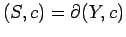 なるスピン定値4次元多様体
なるスピン定値4次元多様体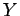 は存在するか?
は存在するか?
- 上記の
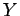 の交叉形式は一意か?
の交叉形式は一意か?
という問題が残る.いずれについてもある場合は正しく,ある場合は正しくないことが
具体例により示せるが、より一般的に答えるにはまだ手段が不足していると思われる。
これ以外の応用についても時間に余裕があればふれたい.
![]() 上の2次形式の中でどのようなものが4次元スピン閉多様体の交叉形式に
なりうるかについてはSeiberg-Witten理論に基づく古田氏の”10/8"定理を
始め深い結果がある。この定理は4次元スピン閉
上の2次形式の中でどのようなものが4次元スピン閉多様体の交叉形式に
なりうるかについてはSeiberg-Witten理論に基づく古田氏の”10/8"定理を
始め深い結果がある。この定理は4次元スピン閉![]() 多様体
多様体![]() に対しても成り立つ
ことが知られており、
に対しても成り立つ
ことが知られており、![]() 上のディラック作用素
上のディラック作用素![]() の指数
の指数
![]() に関する
不等式として与えられる。
に関する
不等式として与えられる。
![]() に対して
に対して
![]() が球面型多様体
が球面型多様体![]() そのものである場合は上記の
そのものである場合は上記の![]() として
として
![]() をとれる。これにより
3次元球面型多様体とそのスピン構造の対
をとれる。これにより
3次元球面型多様体とそのスピン構造の対![]() を境界とする4次元スピン多様体
を境界とする4次元スピン多様体
![]() に対し
に対し
![]() の例がこれらの条件をみたす.ただし,
の例がこれらの条件をみたす.ただし,