4.1 Van Putten’s approach
Relying on a formulation of Maxwell’s equations as a hyperbolic system in divergence form, van
Putten [285] has devised a numerical method to solve the equations of relativistic ideal MHD in flat
spacetime [287 ]. Here we only discuss the basic principles of the method in one spatial dimension. In van
Putten’s approach, the state vector
]. Here we only discuss the basic principles of the method in one spatial dimension. In van
Putten’s approach, the state vector 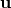 and the fluxes
and the fluxes 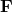 of the conservation laws are decomposed into a
spatially constant mean (subscript 0) and a spatially dependent variational (subscript 1) part,
The RMHD equations then become a system of evolution equations for the integrated variational parts
of the conservation laws are decomposed into a
spatially constant mean (subscript 0) and a spatially dependent variational (subscript 1) part,
The RMHD equations then become a system of evolution equations for the integrated variational parts
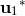 , which reads
together with the conservation condition
The quantities
, which reads
together with the conservation condition
The quantities 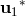 are defined as
They are continuous, and standard methods can be used to integrate the system (53). Van Putten uses a
leapfrog method.
are defined as
They are continuous, and standard methods can be used to integrate the system (53). Van Putten uses a
leapfrog method.
The new state vector 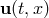 is then obtained from
is then obtained from 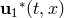 by numerical differentiation.
This process can lead to oscillations in the case of strong shocks and a smoothing algorithm
should be applied. Details of this smoothing algorithm and of the numerical method in one
and two spatial dimensions can be found in [286
by numerical differentiation.
This process can lead to oscillations in the case of strong shocks and a smoothing algorithm
should be applied. Details of this smoothing algorithm and of the numerical method in one
and two spatial dimensions can be found in [286 ] together with results on a large variety of
tests.
] together with results on a large variety of
tests.
Van Putten has applied his method to simulate relativistic hydrodynamic and magneto-hydrodynamic
jets with moderate flow Lorentz factors (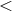 4.25) [288
4.25) [288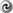 , 291
, 291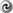 ].
].
![]() is then obtained from
is then obtained from ![]() by numerical differentiation.
This process can lead to oscillations in the case of strong shocks and a smoothing algorithm
should be applied. Details of this smoothing algorithm and of the numerical method in one
and two spatial dimensions can be found in [286
by numerical differentiation.
This process can lead to oscillations in the case of strong shocks and a smoothing algorithm
should be applied. Details of this smoothing algorithm and of the numerical method in one
and two spatial dimensions can be found in [286![]() ] together with results on a large variety of
tests.
] together with results on a large variety of
tests.
![]() 4.25) [288
4.25) [288![]() , 291
, 291![]() ].
].