3.3 The brane viewpoint: A 1+3-covariant analysis
Following [218 ], a systematic analysis can be developed from the viewpoint of a brane-bound observer.
The effects of bulk gravity are conveyed, from a brane observer viewpoint, via the local (
], a systematic analysis can be developed from the viewpoint of a brane-bound observer.
The effects of bulk gravity are conveyed, from a brane observer viewpoint, via the local (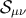 ) and
nonlocal (
) and
nonlocal ( ) corrections to Einstein’s equations. (In the more general case, bulk effects on the brane are
also carried by
) corrections to Einstein’s equations. (In the more general case, bulk effects on the brane are
also carried by  , which describes any 5D fields.) The
, which describes any 5D fields.) The 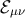 term cannot in general be determined from
data on the brane, and the 5D equations above (or their equivalent) need to be solved in order to find
term cannot in general be determined from
data on the brane, and the 5D equations above (or their equivalent) need to be solved in order to find
 .
.
The general form of the brane energy-momentum tensor for any matter fields (scalar fields, perfect
fluids, kinetic gases, dissipative fluids, etc.), including a combination of different fields, can be covariantly
given in terms of a chosen 4-velocity  as
as
Here 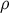 and
and  are the energy density and isotropic pressure, respectively, and
projects into the comoving rest space orthogonal to
are the energy density and isotropic pressure, respectively, and
projects into the comoving rest space orthogonal to 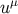 on the brane. The momentum density and
anisotropic stress obey
where angled brackets denote the spatially projected, symmetric, and tracefree part:
In an inertial frame at any point on the brane, we have
where
on the brane. The momentum density and
anisotropic stress obey
where angled brackets denote the spatially projected, symmetric, and tracefree part:
In an inertial frame at any point on the brane, we have
where 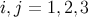 .
.
The tensor  , which carries local bulk effects onto the brane, may then be irreducibly decomposed
as
, which carries local bulk effects onto the brane, may then be irreducibly decomposed
as
This simplifies for a perfect fluid or minimally-coupled scalar field to
The tracefree  carries nonlocal bulk effects onto the brane, and contributes an effective “dark”
radiative energy-momentum on the brane, with energy density
carries nonlocal bulk effects onto the brane, and contributes an effective “dark”
radiative energy-momentum on the brane, with energy density 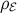 , pressure
, pressure 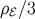 , momentum density
, momentum density
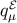 , and anisotropic stress
, and anisotropic stress 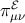 :
:
We can think of this as a KK or Weyl “fluid”. The brane “feels” the bulk gravitational field through this
effective fluid. More specifically:
- The KK (or Weyl) anisotropic stress
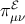 incorporates the scalar or spin-0 (“Coulomb”), the
vector (transverse) or spin-1 (gravimagnetic), and the tensor (transverse traceless) or spin-2
(gravitational wave) 4D modes of the spin-2 5D graviton.
incorporates the scalar or spin-0 (“Coulomb”), the
vector (transverse) or spin-1 (gravimagnetic), and the tensor (transverse traceless) or spin-2
(gravitational wave) 4D modes of the spin-2 5D graviton.
- The KK momentum density
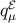 incorporates spin-0 and spin-1 modes, and defines a velocity
incorporates spin-0 and spin-1 modes, and defines a velocity
 of the Weyl fluid relative to
of the Weyl fluid relative to 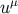 via
via 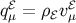 .
.
- The KK energy density
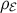 , often called the “dark radiation”, incorporates the spin-0 mode.
, often called the “dark radiation”, incorporates the spin-0 mode.
In special cases, symmetry will impose simplifications on this tensor. For example, it must vanish for a
conformally flat bulk, including 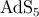 ,
,
The RS models have a Minkowski brane in an  bulk. This bulk is also compatible with an FRW
brane. However, the most general vacuum bulk with a Friedmann brane is Schwarzschild-anti-de Sitter
spacetime [32
bulk. This bulk is also compatible with an FRW
brane. However, the most general vacuum bulk with a Friedmann brane is Schwarzschild-anti-de Sitter
spacetime [32 , 249
, 249 ]. Then it follows from the FRW symmetries that
where
]. Then it follows from the FRW symmetries that
where 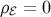 only if the mass of the black hole in the bulk is zero. The presence of the bulk black hole
generates via Coulomb effects the dark radiation on the brane.
only if the mass of the black hole in the bulk is zero. The presence of the bulk black hole
generates via Coulomb effects the dark radiation on the brane.
For a static spherically symmetric brane (e.g., the exterior of a static star or black hole) [72 ],
],
This condition also holds for a Bianchi I brane [221 ]. In these cases,
]. In these cases, 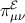 is not determined by the
symmetries, but by the 5D field equations. By contrast, the symmetries of a Gödel brane fix
is not determined by the
symmetries, but by the 5D field equations. By contrast, the symmetries of a Gödel brane fix
 [20].
[20].
The brane-world corrections can conveniently be consolidated into an effective total energy density,
pressure, momentum density, and anisotropic stress:
These general expressions simplify in the case of a perfect fluid (or minimally coupled scalar field, or
isotropic one-particle distribution function), i.e., for 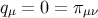 , to
Note that nonlocal bulk effects can contribute to effective imperfect fluid terms even when the matter on
the brane has perfect fluid form: There is in general an effective momentum density and anisotropic stress
induced on the brane by massive KK modes of the 5D graviton.
, to
Note that nonlocal bulk effects can contribute to effective imperfect fluid terms even when the matter on
the brane has perfect fluid form: There is in general an effective momentum density and anisotropic stress
induced on the brane by massive KK modes of the 5D graviton.
The effective total equation of state and sound speed follow from Equations (98) and (99) as
where 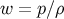 and
and 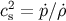 . At very high energies, i.e.,
. At very high energies, i.e.,  , we can generally neglect
, we can generally neglect 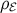 (e.g.,
in an inflating cosmology), and the effective equation of state and sound speed are stiffened:
This can have important consequences in the early universe and during gravitational collapse. For example,
in a very high-energy radiation era,
(e.g.,
in an inflating cosmology), and the effective equation of state and sound speed are stiffened:
This can have important consequences in the early universe and during gravitational collapse. For example,
in a very high-energy radiation era,  , the effective cosmological equation of state is
ultra-stiff:
, the effective cosmological equation of state is
ultra-stiff:  . In late-stage gravitational collapse of pressureless matter,
. In late-stage gravitational collapse of pressureless matter, 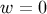 , the
effective equation of state is stiff,
, the
effective equation of state is stiff, 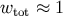 , and the effective pressure is nonzero and dynamically
important.
, and the effective pressure is nonzero and dynamically
important.
![]() as
as ![]() , which carries local bulk effects onto the brane, may then be irreducibly decomposed
as
, which carries local bulk effects onto the brane, may then be irreducibly decomposed
as ![]() carries nonlocal bulk effects onto the brane, and contributes an effective “dark”
radiative energy-momentum on the brane, with energy density
carries nonlocal bulk effects onto the brane, and contributes an effective “dark”
radiative energy-momentum on the brane, with energy density ![]() , pressure
, pressure ![]() , momentum density
, momentum density
![]() , and anisotropic stress
, and anisotropic stress ![]() :
: ![]() ,
, ![]() ],
],
![]() ) and (99
) and (99![]() ) as
) as