1.2.1 で説明した FFT は,周波数領域の添字 k を偶数と奇数とに分ける ことで,半分の長さの DFT に変換するという方法ですが,時間領域の 添字 j を偶数と奇数とに分けることでも半分の長さの DFT
N/2-1 jk k N/2-1 jk
A = Σ a W + W Σ a W
k j=0 2j N/2 j=0 2j+1 N/2
N/2-1 jk k N/2-1 jk
A = Σ a W − W Σ a W
N/2+k j=0 2j N/2 j=0 2j+1 N/2
に分解することができます.次に,この分解による時間間引き FFT ルーチンの 例を示します.
| リスト1.2.2-1. 基数 2 の時間間引き FFT |
|---|
#include <math.h>
void fft(int n, double theta, double ar[], double ai[])
{
int m, mh, i, j, k;
double wr, wi, xr, xi;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
xr = ar[j];
xi = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = xr;
ai[i] = xi;
}
}
theta *= n;
for (mh = 1; (m = mh << 1) <= n; mh = m) {
theta *= 0.5;
for (i = 0; i < mh; i++) {
wr = cos(theta * i);
wi = sin(theta * i);
for (j = i; j < n; j += m) {
k = j + mh;
xr = wr * ar[k] - wi * ai[k];
xi = wr * ai[k] + wi * ar[k];
ar[k] = ar[j] - xr;
ai[k] = ai[j] - xi;
ar[j] += xr;
ai[j] += xi;
}
}
}
}
|
 |
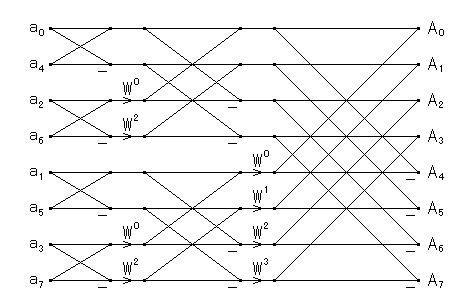
| 図1.2.2-1. 基数 2 の時間間引き FFT のフローグラフ |
|---|
時間間引き FFT は,回転因子 W を掛けてからデータを足し引きするという バタフライ演算からなり,周波数間引きの FFT のデータフローを逆に たどったものに相当します.したがって,時間間引き FFT と周波数間引き FFT の計算量は全く同じで,複素数データの DFT ではどちらを使っても 結果はほぼ同じになります.しかし,拡張 DFT や離散コサイン変換などの 順方向の変換と逆方向の変換が異なる変換では,時間間引きの FFT と 周波数間引きの FFT は互いに逆変換として使われます. 離散コサイン変換では,DCT-II を周波数間引きで,DCT-III を時間間引きで 計算します.実数データの DFT では,順変換を時間間引きで,逆変換を 周波数間引きで計算します.ただし,工夫をすれば実数データの DFT は どちらの間引きでも計算は可能です.これらの設計法は後に示します.
また,畳み込みの計算では,時間間引きの FFT と周波数間引きの FFT の 使い分けによりビット反転並べ替えが省略できます.これは,変換後の データに対するビット反転を省略し,ビット反転の状態で乗算を行い, ビット反転を省略した逆変換でもとに戻すという方法になります.これで 多少の時間の節約ができます.