これまでに示した FFT は,DFT の添字を偶数と奇数に分けることで, 半分の長さの DFT に分解するという方法に基づいています.当然これは 拡張することができ,例えば,R で割り切れる長さの DFT は,1/R の長さの R 個の DFT に分解することができます.一般に基数 R の分解は
N/R-1 R-1 jk
A = Σ ( Σ a ) W
Rk j=0 r=0 Nr/R+j N/R
N/R-1 R-1 r j jk
A = Σ ( Σ a W ) W W
Rk+1 j=0 r=0 Nr/R+j R N N/R
N/R-1 R-1 2r 2j jk
A = Σ ( Σ a W ) W W
Rk+2 j=0 r=0 Nr/R+j R N N/R
・・・
のようにします.一般には
N/R-1 R-1 mr mj jk
A = Σ ( Σ a W ) W W
Rk+m j=0 r=0 Nr/R+j R N N/R
となります.この分解を繰り返すことで,基数 R の FFT が構成されます. この分解の式をよく見ると,長さ N の一次元データ a_j は,R × N/R の 二次元データ a_r,j = a_(N/R)r+j に変換されています.この変換により, 長さ N の DFT は,二重にネストされた長さ N/R の DFT と,長さ R の DFT に分解されます.途中の係数 W_N^mj は,バタフライ演算での 回転因子で,Cooley-Tukey 型 FFT 特有のものです.
次に,この分解による FFT の演算量について考えてみます.長さ N を R の整数乗と仮定して,この分解を log_R(N) 回繰り返すことを考えます. このときの複素乗算回数は
N log N
--- ------- ((R-1) + (長さ R の DFT の乗算回数))
R log R
となることがわかります.これは,基数 R の 1 バタフライルーチンの 乗算回数です.もし,長さ R の DFT の計算に R^2 の乗算回数が必要であると 仮定しても,全体の乗算回数は N*log(N) 回のオーダーしか必要としません. また,この仮定のもとで上の乗算回数の式は,R = e (自然対数の底) で最小と なり,e = 2.718... に近い R = 3 が最適な基数ということになります. これは,Cooley and Tukey による最初の論文でも示されています.しかし 実際には,長さが 2 または 4 の DFT は,±1 または ±i の乗算のみで 実行でき,この乗算は省略できます.したがって,基数 4 の算法は, 基数 2 のに比べて乗算回数が 3/4 に減少します.さらに,基数 8 では 2/3 に,基数 16 では 5/8 に減少し,基数を大きくすると乗算回数は減少する 傾向にあります.一方,実数の加算回数は,基数が 4 のときに最小に なります.例として,基数 4 のルーチンを以下に示します.
| リスト1.2.3-1. 基数 4 の FFT |
|---|
#include <math.h>
void fft(int n, double ar[], double ai[])
{
int m, mq, i, j, j1, j2, j3, k;
double theta, w1r, w1i, w2r, w2i, w3r, w3i;
double x0r, x0i, x1r, x1i, x2r, x2i, x3r, x3i;
/* ---- radix 4 butterflies ---- */
theta = -8 * atan(1.0) / n;
for (m = n; (mq = m >> 2) >= 1; m = mq) {
for (i = 0; i < mq; i++) {
w1r = cos(theta * i);
w1i = sin(theta * i);
w2r = cos(theta * 2 * i);
w2i = sin(theta * 2 * i);
w3r = cos(theta * 3 * i);
w3i = sin(theta * 3 * i);
for (j = i; j < n; j += m) {
j1 = j + mq;
j2 = j1 + mq;
j3 = j2 + mq;
x0r = ar[j] + ar[j2];
x0i = ai[j] + ai[j2];
x1r = ar[j] - ar[j2];
x1i = ai[j] - ai[j2];
x2r = ar[j1] + ar[j3];
x2i = ai[j1] + ai[j3];
x3r = ar[j3] - ar[j1];
x3i = ai[j3] - ai[j1];
ar[j] = x0r + x2r;
ai[j] = x0i + x2i;
x0r = x0r - x2r;
x0i = x0i - x2i;
ar[j1] = w2r * x0r - w2i * x0i;
ai[j1] = w2r * x0i + w2i * x0r;
x0r = x1r - x3i;
x0i = x1i + x3r;
ar[j2] = w1r * x0r - w1i * x0i;
ai[j2] = w1r * x0i + w1i * x0r;
x0r = x1r + x3i;
x0i = x1i - x3r;
ar[j3] = w3r * x0r - w3i * x0i;
ai[j3] = w3r * x0i + w3i * x0r;
}
}
theta *= 4;
}
/* ---- radix 2 butterflies (n % 4 == 2) ---- */
if (m == 2) {
for (j = 0; j < n; j += 2) {
x0r = ar[j] - ar[j + 1];
x0i = ai[j] - ai[j + 1];
ar[j] += ar[j + 1];
ai[j] += ai[j + 1];
ar[j + 1] = x0r;
ai[j + 1] = x0i;
}
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
x0r = ar[j];
x0i = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = x0r;
ai[i] = x0i;
}
}
}
|
 |
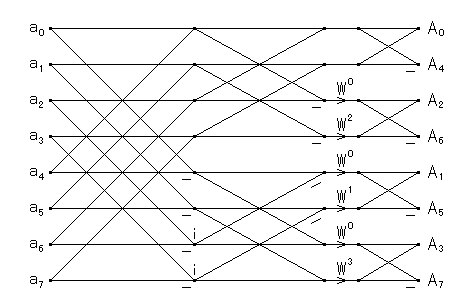
| 図1.2.3-1. 基数 4 の FFT のフローグラフ |
|---|
このルーチンは,基数 4 と基数 2 の混合基数ルーチンです.すなわち, N が 4 の整数乗で割り切れないときは,最後に基数 2 のバタフライ演算が 付け足されます.さらに,4 進数のワード反転と 2 進数のビット反転との 混合を避けるため,基数 4 のバタフライ演算の二番目と三番目の入力を入れ 換え,常にビット反転になるようにしてあります.これらの大きいの基数の FFT は,小さいの基数のルーチンの変形でも機械的に得ることができます. 例えば,基数 4 のルーチンは,基数 2 のルーチンのバタフライ演算の外側の 二つのループを同時に展開し,この 4 個のバタフライ演算に含まれる 回転因子をくくり出し,3 個の回転因子に減らしたものに相当します. この技法は,可換な加算と乗算の演算を交換し,乗算部の演算をひとまとめに するという方法で,Winograd DFT アルゴリズムや,Vector-Radix FFT での 演算の削減技法と似ています.
次に,この基数 4 の FFT の演算量について考えます.N 点の複素 DFT の 計算に必要な実数乗算回数 μ と実数加算回数 α は次のようになります.
3
μ = --- N log N - 5N + 8
2
11 13 8
α = ---- N log N - ---- N + ---
4 6 3
ただし,これは 5 バタフライルーチンを用いて不要な演算を取り除き, 複素乗算を 4 回の実数乗算と 2 回の実数加算で計算したときの値です. これは,基数 2 の FFT に比べて乗算回数が約 3/4 に減り,加算回数が 約 11/12 に減っています.
次に,長さが 2 の整数乗以外の FFT について考えます.実際の 計算では,DFT の長さは 3 の倍数や 10 の倍数などに選ばれることが よくあります.このとき,混合基数 FFT を用います.もし,DFT の長さ N が特定の因数に分解できることがわかっている場合は,それらの因数の 基数の演算をあらかじめ用意し,組み合わせて使います.さらに,N の因数が あらかじめわからない場合は可変長の基数を用います.例として,任意の 長さの FFT ルーチンを示します.
| リスト1.2.3-2. 任意の長さの FFT |
|---|
/*
F[k]=Σ_j=0^n-1 a[j]*exp(±2*pi*i*j*k/n),0<=k<n を計算する.
n はデータ数で任意, theta は ±2*PI/n,
ar[0...n-1], ai[0...n-1], はデータの実部, 虚部,
tmpr[0...n-1], tmpi[0...n-1] は作業領域.
*/
#include <math.h>
void fft(int n, double theta, double ar[], double ai[],
double tmpr[], double tmpi[])
{
int radix, n_radix, j, m, r;
double xr, xi, wr, wi;
if (n <= 1) return;
/* ---- factorization ---- */
for (radix = 2; radix * radix <= n; radix++) {
if (n % radix == 0) break;
}
if (n % radix != 0) radix = n;
n_radix = n / radix;
/* ---- butterflies ---- */
for (j = 0; j < n_radix; j++) {
for (m = 0; m < radix; m++) {
xr = ar[j];
xi = ai[j];
for (r = n_radix; r < n; r += n_radix) {
wr = cos(theta * m * r);
wi = sin(theta * m * r);
xr += wr * ar[r + j] - wi * ai[r + j];
xi += wr * ai[r + j] + wi * ar[r + j];
}
wr = cos(theta * m * j);
wi = sin(theta * m * j);
tmpr[m * n_radix + j] = xr * wr - xi * wi;
tmpi[m * n_radix + j] = xi * wr + xr * wi;
}
}
for (r = 0; r < n; r += n_radix) {
fft(n_radix, theta * radix, &tmpr[r], &tmpi[r], ar, ai);
}
for (j = 0; j < n_radix; j++) {
for (m = 0; m < radix; m++) {
ar[radix * j + m] = tmpr[n_radix * m + j];
ai[radix * j + m] = tmpi[n_radix * m + j];
}
}
}
|
このルーチンは,長さ R の短い DFT を R^2 の計算量の算法で行っています. しかも,再帰呼び出しを用い,三角関数はその場で計算するという無駄の 多いルーチンです.しかし,演算量のオーダーは他の実用的な改良を行った Cooley-Tukey 型の混合基数ルーチンと同じです.一般に,DFT の長さ N が 合成数で小さい数の素因数に分解されるならば,混合基数 FFT の演算量は N*log(N) に比例する程度になります.しかし,DFT の長さが素数のときは 最悪となり,演算量は N^2 のオーダーになります.