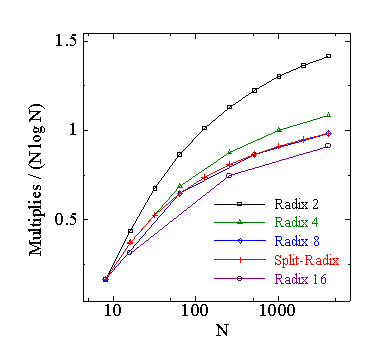
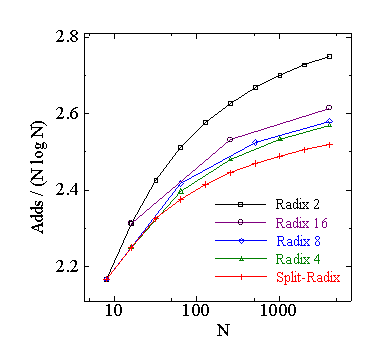
まず,Cooley-Tukey 型 FFT の演算量の比較を行ってみます.基数 2, 4, 8, 16 の Cooley-Tukey FFT と,Split-radix FFT の実数乗算回数と 実数加算回数の表を次に示します.この演算量は,複素数乗算を 4 回の 実数乗算と 2 回の実数加算で計算し,すべての不要な乗算を除去する 5 バタフライルーチンを用いた値です.
| リスト1.2.6-1. 複素 FFT に必要な実数の乗算と加算の回数 |
|---|
| radix 2 FFT | radix 4 FFT | radix 8 FFT | radix 16 FFT |Split-Radix FFT|
N | Mul Add | Mul Add | Mul Add | Mul Add | Mul Add |
-------+---------------+---------------+---------------+---------------+---------------+
2 | 0 4 | - - | - - | - - | 0 4 |
4 | 0 16 | 0 16 | - - | - - | 0 16 |
8 | 4 52 | - - | 4 52 | - - | 4 52 |
16 | 28 148 | 24 144 | - - | 20 148 | 24 144 |
32 | 108 388 | - - | - - | - - | 84 372 |
64 | 332 964 | 264 920 | 248 928 | - - | 248 912 |
128 | 908 2308 | - - | - - | - - | 660 2164 |
256 | 2316 5380 | 1800 5080 | - - | 1528 5184 | 1656 5008 |
512 | 5644 12292 | - - | 3992 11632 | - - | 3988 11380 |
1024 | 13324 27652 | 10248 25944 | - - | - - | 9336 25488 |
2048 | 30732 61444 | - - | - - | - - | 21396 56436 |
4096 | 69644 135172 | 53256 126296 | 48280 126832 | 44856 128480 | 48248 123792 |
|
 |
 |
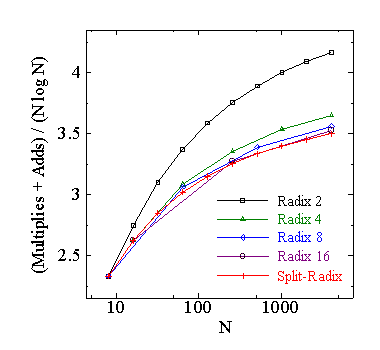
| 図1.2.6-1. 各 FFT の乗算と加算回数 | |
|---|---|
 |
| 図1.2.6-2. 各 FFT の総演算回数 |
|---|
この表より,乗算回数は大きい基数の FFT が少なくなります.加算回数は, Split-Radix FFT が最も少なく,次に基数 4 の FFT となります.加算回数と 乗算回数を足した総演算回数は Split-Radix FFT が最も少なくなります. 次に,バタフライの数に対する演算回数の表を示します.
| リスト1.2.6-2. バタフライの数に対する実数乗算と加算の回数 |
|---|
radix 2 FFT
| 1 butterfly | 2 butterflies | 3 butterflies | 5 butterflies |
N | Mul Add | Mul Add | Mul Add | Mul Add |
-------+---------------+---------------+---------------+---------------+
2 | 4 6 | 0 4 | 0 4 | 0 4 |
4 | 16 24 | 4 18 | 0 16 | 0 16 |
8 | 48 72 | 20 58 | 8 52 | 4 52 |
16 | 128 192 | 68 162 | 40 148 | 28 148 |
32 | 320 480 | 196 418 | 136 388 | 108 388 |
64 | 768 1152 | 516 1026 | 392 964 | 332 964 |
128 | 1792 2688 | 1284 2434 | 1032 2308 | 908 2308 |
256 | 4096 6144 | 3076 5634 | 2568 5380 | 2316 5380 |
512 | 9216 13824 | 7172 12802 | 6152 12292 | 5644 12292 |
1024 | 20480 30720 | 16388 28674 | 14344 27652 | 13324 27652 |
2048 | 45056 67584 | 36868 63490 | 32776 61444 | 30732 61444 |
4096 | 98304 147456 | 81924 139266 | 73736 135172 | 69644 135172 |
radix 4 FFT
| 1 butterfly | 2 butterflies | 3 butterflies | 5 butterflies |
N | Mul Add | Mul Add | Mul Add | Mul Add |
-------+---------------+---------------+---------------+---------------+
4 | 12 22 | 0 16 | 0 16 | 0 16 |
16 | 96 176 | 36 146 | 28 144 | 24 144 |
64 | 576 1056 | 324 930 | 284 920 | 264 920 |
256 | 3072 5632 | 2052 5122 | 1884 5080 | 1800 5080 |
1024 | 15360 28160 | 11268 26114 | 10588 25944 | 10248 25944 |
4096 | 73728 135168 | 57348 126978 | 54620 126296 | 53256 126296 |
radix 8 FFT
| 1 butterfly | 2 butterflies | 3 butterflies | 5 butterflies |
N | Mul Add | Mul Add | Mul Add | Mul Add |
-------+---------------+---------------+---------------+---------------+
8 | 32 66 | 4 52 | 4 52 | 4 52 |
64 | 512 1056 | 260 930 | 252 928 | 248 928 |
512 | 6144 12672 | 4100 11650 | 4028 11632 | 3992 11632 |
4096 | 65536 135168 | 49156 126978 | 48572 126832 | 48280 126832 |
|
この表より,バタフライの数が基数と同じくらい演算量に寄与している ことがわかります.また,大きい基数では演算量に対するバタフライの数の 寄与は小さくなります.基数 4 の FFT では,バタフライの数が 3 を越えると 演算量はほとんど減少しなくなり,基数 8 の FFT では,バタフライの数が 2 を越えると演算量はほとんど減少しなくなります.
次に,実際の FFT の設計について考えます.Cooley-Tukey 型 FFT の 演算量を削減するための基本的な方法は,バタフライの数を増やして, 基数を大きくすることです.しかし,これらの方法をむやみに用いると, バタフライループが巨大で複雑なものになってしまいます.このとき,CPU の レジスタやキャッシュに入り切らない場合は,極端に遅くなります.そこで, ハードウエアやコンパイラに応じて適切なバタフライ数や基数を決めることが 必要になります.個人的な経験では,基数 4 の 3 バタフライルーチンまたは 基数 8 の 2 バタフライルーチンが多くの場合で最適となるようです.また, Split-Radix FFT は Cooley-Tukey 型 FFT の中で演算量は最小ですが, ループ構造が複雑になるため,必ずしも有利になるとはいえないようです.
大きい基数の FFT の設計では,N の値が飛び飛びになるのを防ぐために, 混合基数ルーチンにします.このとき,演算量を少なくするためにちょっとした 注意が必要です.例えば,周波数間引きの基数 4, 2 の混合基数ルーチンで, N=128 のときは因数を 4,4,4,2 という順に分解し実行します.時間間引きの 場合は逆の順にします.また,周波数間引きの基数 8, 4, 2 の混合基数 ルーチンで,N=128 の場合は 8,8,2 という分解でなく,8,4,4 という 変則的な分解をします.演算量を少なくする分解には順序があるので 注意してください.
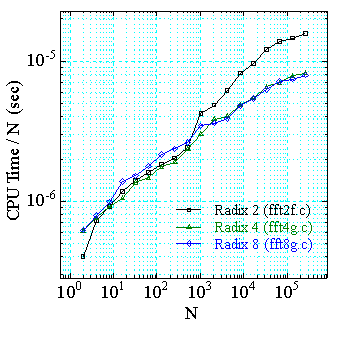
基数 2 の 2 バタフライルーチンと,基数 2,4 の 3 バタフライルーチン, 基数 2,4,8 の 3 バタフライルーチンの具体的な計算時間の比較は次の図の ようになります.これらは,FFT パッケージ内の ルーチンです.
 |
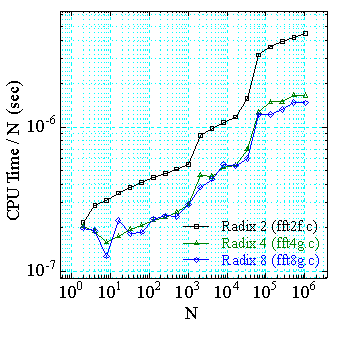 |
| Pentium 90 MHz | Ultra SPARC 200 MHz |
|---|---|
| 図1.2.6-2. 各 FFT の一点あたりの実行時間 | |
乗算回数を削減する別の方法に,複素乗算を 3 回の実数乗算と 3 回の実数加算で計算する方法があります.これは よく知られた方法で,通常の複素乗算
yr = xr * wr - xi * wi
yi = xi * wr + xr * wi
を次のように変形することで得られます.
tmp = (xr + xi) * wr
yr = tmp - xi * (wr + wi)
yi = tmp - xr * (wr - wi)
ここで,wr+wi, wr-wi はあらかじめ計算しておきます.この方法で, 乗算回数は 3/4 に減りますが,乗算回数と加算回数を足した総演算量は 同じです.この方法は,乗算が加算に比べて高くつく場合に有効です. しかし,最近の計算機では乗算と加算のコストはそれほど違いません. むしろ,計算が複雑になることから,多くの状況でこの方法は不利になる ようです.
FFT の設計では,四則演算以外に三角関数の計算が問題になります. 通常,三角関数はあらかじめ計算して表にしておきます.この三角関数表は, データと同じ程度の大きさが必要です.余計なメモリを使いたくなく,かつ 高速に計算したいのならば,三角関数は簡単な漸化式で計算します.例えば, 等間隔の角度の三角関数は,三項漸化式
cos((k+1)*h) = -(2*sin(h)) * sin(k*h) + cos((k-1)*h)
sin((k+1)*h) = (2*sin(h)) * cos(k*h) + sin((k-1)*h)
で計算できます.(2*sin(h)) と初期の項はあらかじめ計算しておきます.この 方法は,三角関数 1 回あたり,1 回の乗算と 1 回の加算を必要とします. これと同じ計算量をもつ他の方法に,チェビシェフ多項式の三項漸化式
cos((k+1)*h) = (2*cos(h)) * cos(k*h) - cos((k-1)*h)
sin((k+1)*h) = (2*cos(h)) * sin(k*h) - sin((k-1)*h)
を用いる方法があります.しかし,この方法は桁落ち防止の変形が必要で, 加算が 1 回増えてしまいます.このほかにもいろいろな漸化式があります. 一般に,漸化式による三角関数の計算は,丸め誤差の影響を受けます.非常に 長い FFT の計算では,この丸め誤差は蓄積されて大きくなります.最悪の 場合,この丸め誤差は長さ N に比例します.しかし,経験では N=8192 で 1 桁から 2 桁くらいの精度が落ちる程度で済みます.
次に,FFT ルーチンでのデータ転送について考えます.階層的な メモリ構造をもつ計算機では,演算量よりもメモリアクセスの方が重要に なります.これは,FFT に限らず大きな配列を扱う計算には常につきまとう 問題です.例えば,CPU にキャッシュを持つような計算機では,外部の メモリアクセスに多くの時間を費やします.このような場合は,多少の 演算量を犠牲にしても,メモリアクセスを局所化した方がずっと高速に なります.この局所化の最も単純な方法は,複素数データの実部と虚部を 隣り合わせにすることです.これは,以外と効果があるようです.また, メモリアクセスの局所化は in-place 演算にすることでもなされます. in-place 演算は,非 in-place 演算に比べて半分のデータの読み書きに なります.しかし,これと引き換えに普通の in-place 演算ではスクランブラ が必要になります.このスクランブルでのメモリアクセスはランダムに近く, 通常スクランブルに要する時間は全体の時間の一割以上になってしまいます. 確実なメモリアクセスの高速化は,最も内側のバタフライループで メモリアクセスを連続にすることです.この連続化には,ちょっとした ループ構造の変形やアルゴリズムの変更が必要になります.このとき, 三角関数表のデータ参照も同時に考えなければなりません.さらに, キャッシュミスを最小限に減らすために,バタフライを単純な ループではなく階層的にアクセスする tree 構造にする場合があります. これは,FFT の原理に従って再起呼び出しをすることで実現できますが, 基数の選び方や細かいインプリメントの仕方によって性能が大きく異なるので 注意が必要です.このようなメモリの高速化は,ハードウエアとコンパイラに 依存するため,実際に使用するシステムで実行してみる必要があります.