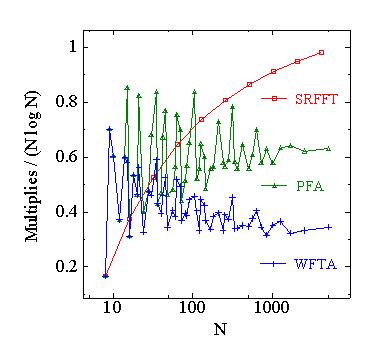
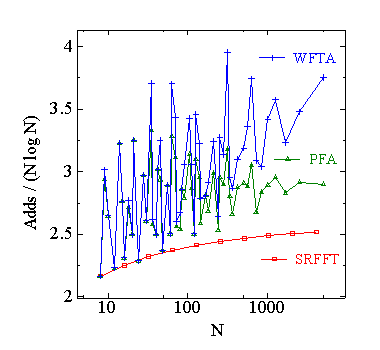
まず,PFA と WFTA の演算量の比較を行います.次の表に,長さ N に対する PFA と WFTA の実乗算回数と実加算回数と総演算回数を示します.WFTA では, 1 による乗算は無視し,加算回数が最も少なくなる因数の分解を行っています.
| リスト1.3.5-1. PFA と WFTA の実数乗算と加算の回数 |
|---|
| PFA | WFTA |
N | Mul Add Total | Mul Add Total |
-------+-----------------------+-----------------------+
2 | 0 4 4 | 0 4 4 |
3 | 4 12 16 | 4 12 16 |
4 | 0 16 16 | 0 16 16 |
5 | 10 34 44 | 10 34 44 |
6 | 8 36 44 | 8 36 44 |
7 | 16 72 88 | 16 72 88 |
8 | 4 52 56 | 4 52 56 |
9 | 20 84 104 | 20 86 106 |
10 | 20 88 108 | 20 88 108 |
12 | 16 96 112 | 16 96 112 |
14 | 32 172 204 | 32 172 204 |
15 | 50 162 212 | 34 162 196 |
16 | 20 148 168 | 20 148 168 |
18 | 40 204 244 | 40 208 248 |
20 | 40 216 256 | 40 216 256 |
21 | 76 300 376 | 52 300 352 |
24 | 44 252 296 | 36 252 288 |
28 | 64 400 464 | 64 400 464 |
30 | 100 384 484 | 68 384 452 |
35 | 150 598 748 | 106 666 772 |
36 | 80 480 560 | 80 488 568 |
40 | 100 532 632 | 84 532 616 |
42 | 152 684 836 | 104 684 788 |
45 | 190 726 916 | 130 804 934 |
48 | 124 636 760 | 92 636 728 |
56 | 156 940 1096 | 132 940 1072 |
60 | 200 888 1088 | 136 888 1024 |
63 | 284 1236 1520 | 196 1394 1590 |
70 | 300 1336 1636 | 212 1472 1684 |
72 | 196 1140 1336 | 164 1156 1320 |
80 | 260 1284 1544 | 200 1352 1552 |
84 | 304 1536 1840 | 208 1536 1744 |
90 | 380 1632 2012 | 260 1788 2048 |
105 | 590 2214 2804 | 322 2418 2740 |
112 | 396 2188 2584 | 308 2332 2640 |
120 | 460 2076 2536 | 276 2076 2352 |
126 | 568 2724 3292 | 392 3040 3432 |
140 | 600 2952 3552 | 424 3224 3648 |
144 | 500 2676 3176 | 380 2880 3260 |
168 | 692 3492 4184 | 420 3492 3912 |
180 | 760 3624 4384 | 520 3936 4456 |
210 | 1180 4848 6028 | 644 5256 5900 |
240 | 1100 4812 5912 | 632 5016 5648 |
252 | 1136 5952 7088 | 784 6584 7368 |
280 | 1340 6604 7944 | 852 7148 8000 |
315 | 2050 8322 10372 | 1186 10336 11522 |
336 | 1636 7908 9544 | 956 8340 9296 |
360 | 1700 8148 9848 | 1044 8772 9816 |
420 | 2360 10536 12896 | 1288 11352 12640 |
504 | 2524 13164 15688 | 1572 14428 16000 |
560 | 3100 14748 17848 | 1928 17168 19096 |
630 | 4100 17904 22004 | 2372 21932 24304 |
720 | 3940 18276 22216 | 2360 21132 23492 |
840 | 5140 23172 28312 | 2580 24804 27384 |
1008 | 5804 29100 34904 | 3548 34416 37964 |
1260 | 8200 38328 46528 | 4744 46384 51128 |
1680 | 11540 50964 62504 | 5816 58224 64040 |
2520 | 17660 82956 100616 | 9492 99068 108560 |
5040 | 39100 179772 218872 | 21368 232668 254036 |
|
この表から WFTA は N=15 以上で PFA に対して効果を発揮することが わかります.N=100 程度までの長さならば WFTA は加算回数の増加無しで 乗算回数を減らすことができます.しかし,N が 1000 を越すと WFTA は 乗算回数の減少よりも加算回数の増加の方が上回ってしまいます. WFTA は乗算が加算よりも非常に高くつく場合に有効な方法です. 総演算量で考えると WFTA は PFA と比較して必ずしも有利にはなりません. 実際の Prime Factor 型 FFT の設計では,短い長さに関しては WFTA で 設計しておいて,それを PFA で組み合わせて長い長さに対応させる という方法が用いられることがあるようです.しかし,この方法による 高速算法の設計は,相当な努力を必要とします.
次に,長さ N に対する PFA と WFTA の実乗算回数と実加算回数と 総演算回数の図を示します.参考のため Split-Radix FFT の演算回数も 入れてあります.
 |
 |
| 図1.3.5-1. 各 FFT の乗算と加算回数 | |
|---|---|
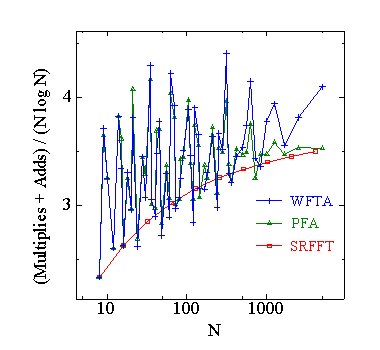 |
| 図1.3.5-2. 各 FFT の総演算回数 |
|---|
実乗算回数では WFTA が最も少なく,次に PFA となります.実加算回数では Split-Radix FFT が最も少なく,次に PFA となります.総演算回数では, PFA と WFTA と Split-Radix FFT の三つはほぼ同じになります.
次に,演算量以外の計算について考えます.WFTA は乗算部の前後に 加算ブロックがあり,PFA に比べて段数が倍になります.したがって, メモリアクセスが倍になり,データの添字の処理も複雑になります. WFTA はまた,非常に大きな乗算係数の表を必要とします.N=1000 程度の 長さの計算では,この表の大きさは 3000 以上の長さになります.一方, PFA では必要な三角関数表のデータきわめて少なく,N=1000 程度で数十程度で 済みます.また,PFA はセルフソートの in-place 演算ができるのに対して, WFTA は in-place 演算ができません.したがって,WFTA は通常の計算機では オーバーヘッドが大きく,DSP チップなどのハードウエア的な目的にしか 使われないようです.
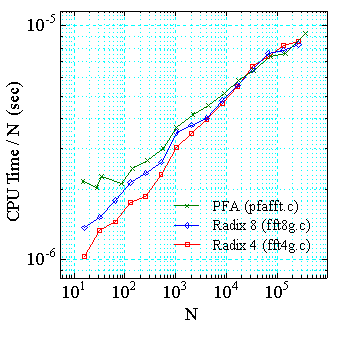
次に,実際の計算機で高速になるように設計された Cooley-Tukey 型 FFT と Prime Factor 型 FFT の実行時間 (CPU 時間) の比較を示します.比較に用いた 計算機は,Pentium 90 MHz の PC と SUN / Ultra-SPARC 200 MHz の二つで, コンパイラは gcc 2.7.2 と SUN WS cc 4.2.1 です.比較を行ったルーチンは, 3 バタフライの基数 2,4 または基数 2,4,8 のループ構造の Cooley-Tukey 型 FFT ルーチンとセルフソートの in-place 型 PFA ルーチンで,ともに高速に 設計されたものです.
 |
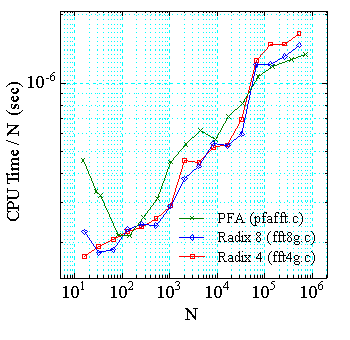 |
| Pentium 90 MHz | Ultra SPARC 200 MHz |
|---|---|
| 図1.3.5-3. 各 FFT の一点あたりの実行時間 | |
この例から,高速に設計された Cooley-Tukey 型 FFT と Prime Factor 型 FFT の実行時間はほぼ互角になるようです.