対称なデータの DFT は,FFT を用いる多くの状況で現れます.この 対称なデータの DFT は離散コサイン変換に相当します.これに対して 何も考えずに FFT を行うと,半分のデータと計算量が無駄になります. ここでは,離散コサイン変換,離散サイン変換に対する無駄のない 高速算法を考えます.
通常,離散コサイン変換・離散サイン変換は離散化方法の違いにより, 次の四つのタイプに分けられます.これらのタイプの変換はすべて直交変換で, 積分で書かれた連続版のコサイン変換やサイン変換でのいろいろな性質を 保存します.
| リスト2.3.1-1. DCT のタイプ | |
|---|---|
| DCT-I |
1/2 N
A = (2/N) Σ s s a cos(πjk/N) , 0 <= k <= N
k j=0 j k j
|
| DCT-II |
1/2 N-1
A = (2/N) Σ s a cos(π(j+1/2)k/N) , 0 <= k <= N-1
k j=0 k j
|
| DCT-III |
1/2 N-1
A = (2/N) Σ s a cos(πj(k+1/2)/N) , 0 <= k <= N-1
k j=0 j j
|
| DCT-IV |
1/2 N-1
A = (2/N) Σ a cos(π(j+1/2)(k+1/2)/N) , 0 <= k <= N-1
k j=0 j
|
| リスト2.3.1-2. DST のタイプ | |
|---|---|
| DST-I |
1/2 N-1
A = (2/N) Σ a sin(πjk/N) , 1 <= k <= N-1
k j=1 j
|
| DST-II |
1/2 N
A = (2/N) Σ s a sin(π(j-1/2)k/N) , 1 <= k <= N
k j=1 k j
|
| DST-III |
1/2 N
A = (2/N) Σ s a sin(πj(k-1/2)/N) , 1 <= k <= N
k j=1 j j
|
| DST-IV |
1/2 N-1
A = (2/N) Σ a sin(π(j+1/2)(k+1/2)/N) , 0 <= k <= N-1
k j=0 j
|
上の表で,s_j は正規化の係数で
s = s = sqrt(1/2)
0 N
s = 1 , 0 < j < N
j
となります.このスケーリングの方法は,書物によって異なることがあるので 注意してください.高速演算の説明では簡単のため,このスケーリングは 無視します.
次に,DCT/DST の性質について少し考えます.DCT-I は対称データの DFT に 相当し,DST-I は反対称データの DFT に相当します.DCT-II, DCT-III, DCT-IV は対称データの拡張 DFT に相当し,DST-II, DST-III, DST-IV は 反対称データの拡張 DFT に相当します.特に,DCT-II はチェビシェフ補間の 係数を求める変換に相当し,DCT-III はチェビシェフ補間の係数から補間点を 求める変換に相当します.タイプ II, III, IV の変換は N 点の変換であるのに 対して,DCT-I は N+1 点の変換で,DST-I は N-1 点の変換になり非対称と なります.タイプ I とタイプ IV の変換はそれ自身が逆変換となり, タイプ II とタイプ III の変換はお互いが逆変換となります.画像圧縮などの 分野では,離散コサイン変換は DCT-II をさし,逆離散コサイン変換は DCT-III をさします.また重要な性質として,タイプ II, III, IV の サイン変換はデータの符号の付け替えと並べ替えでコサイン変換になります. たとえば,偶数番目の入力データの符号を付け替えた DST-II は,出力を 逆に並べ替えた DCT-II に相当します.DST-III, DST-IV に対しても同様に, 符号の付け換えと添字の変換で DCT-III, DCT-IV になります.すなわち, II, III, IV の変換に関する FFT アルゴリズムはコサイン変換だけで 十分ということになります.
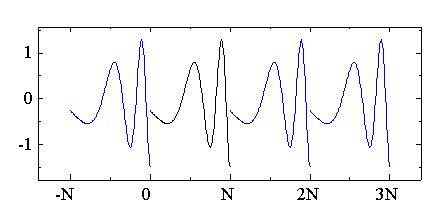
次に,DFT と DCT の直感的な違いについて考えます.長さ N の DFT は, N の周期で無限に拡張した関数のフーリエ変換に相当します.すなわち, 長さ N のデータの DFT を計算する場合,N の周期で無限に繰り返す関数の 周波数を計算していることになります.それに対して,長さ N の DCT は N または N+1/2 を鏡の面とみなして対称に折り返したデータの DFT または 拡張 DFT に相当します.したがって,DCT は N の周期で折り返した関数の 周波数を計算していることになります.
 |
| 図2.3.1-1. DFT のデータの拡張 |
|---|
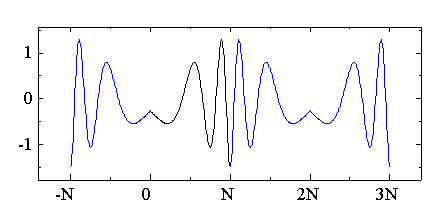 |
| 図2.3.1-2. DCT のデータの拡張 |
|---|
DCT はこのような対称データのフーリエ変換に相当するので,変換後のデータの 虚部が消えて実数の変換になります.DFT は一般につなぎ目で不連続に 拡張されますが,DCT は連続に拡張されます.DFT では不連続な点に含まれる 高周波のノイズを取り除くために窓関数をかけたりするのですが,DCT は 連続になるために窓関数がなくても高周波成分はある程度小さくなります. これは,DCT が画像データの圧縮などによく用いられる主な理由と 考えられます.