Vector-Radix FFT は,一次元の Cooley-Tukey 型 FFT の分解を そのまま多次元に拡張したものです.この Vector-Radix FFT は, 同じ基数の Row-Column 法による FFT と比較して複素数乗算回数が 少なくなるという利点があります.
例えば,二次元 DFT
N1-1 N2-1 j1 k1 j2 k2
A = Σ Σ a W W
k1, k2 j1=0 j2=0 j1, j2 N1 N2
に対する,周波数間引きの基数 2 の分解は次のようになります.
N1/2-1 N2/2-1 j1 k1 j2 k2
A = Σ Σ p W W
2k1, 2k2 j1=0 j2=0 j1, j2 N1/2 N2/2
N1/2-1 N2/2-1 j1 k1 j2 k2
A = Σ Σ q W W
2k1, 2k2+1 j1=0 j2=0 j1, j2 N1/2 N2/2
N1/2-1 N2/2-1 j1 k1 j2 k2
A = Σ Σ r W W
2k1+1, 2k2 j1=0 j2=0 j1, j2 N1/2 N2/2
N1/2-1 N2/2-1 j1 k1 j2 k2
A = Σ Σ s W W
2k1+1, 2k2+1 j1=0 j2=0 j1, j2 N1/2 N2/2
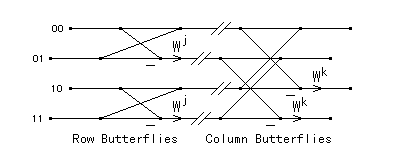
すなわち,Vector-Radix FFT は行方向と列方向の分解を同時に行ったものに 相当します.ここで,p,q,r,s は一次元の分解と同様に a から 求められます.この Vector-Radix FFT のバタフライは,次の図のように なります.比較のため,基数 2 の Row-Column 法による FFT のバタフライも 示します.
 |
| 図3.2-1. Row-Column FFT のバタフライ |
|---|
 |
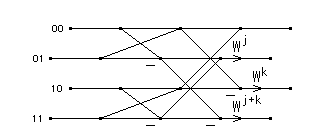
| 図3.2-2. Vector-Radix FFT のバタフライ |
この図から,Vector Radix FFT の一つのバタフライは,Row-Column FFT の 四つのバタフライに相当することがわかります.このバタフライを比較すると, Row-Column FFT では四つあった複素数乗算が,Vector-Radix FFT では演算の 順序の交換により,三つに減っていることがわかります.したがって, 基数 2 の二次元 Vector-Radix FFT は,Row-Column FFT に比べて複素数 乗算回数が 3/4 に減ります.
次に,基数 2 の N x N 二次元 Vector-Radix FFT のルーチン例を示します.
| リスト3.2-1. 基数 2 の二次元 Vector-Radix FFT |
|---|
/*
n x n 二次元 DFT :
F[k1][k2]=Σ_j1=0^n-1 Σ_j2=0^n-1
a[j1][a2] * exp(±2*pi*i*j1*k1/n)
* exp(±2*pi*i*j2*k2/n)
を計算する.
n はデータ数で 2 の整数乗, theta は ±2*pi/n .
*/
#include <math.h>
void fft2dr(int n, double theta, double **ar, double **ai)
{
int m, mh, i1, i2, j1, j2, k1, k2;
double w1r, w1i, w2r, w2i, w12r, w12i;
double xr, xi, xjjr, xjji, xkjr, xkji, xjkr, xjki, xkkr, xkki;
for (m = n; (mh = m >> 1) >= 1; m = mh) {
for (i1 = 0; i1 < mh; i1++) {
w1r = cos(theta * i1);
w1i = sin(theta * i1);
for (i2 = 0; i2 < mh; i2++) {
w2r = cos(theta * i2);
w2i = sin(theta * i2);
w12r = cos(theta * (i1 + i2));
w12i = sin(theta * (i1 + i2));
for (j1 = i1; j1 < n; j1 += m) {
k1 = j1 + mh;
for (j2 = i2; j2 < n; j2 += m) {
k2 = j2 + mh;
xjjr = ar[j1][j2] + ar[k1][j2];
xjji = ai[j1][j2] + ai[k1][j2];
xkjr = ar[j1][j2] - ar[k1][j2];
xkji = ai[j1][j2] - ai[k1][j2];
xjkr = ar[j1][k2] + ar[k1][k2];
xjki = ai[j1][k2] + ai[k1][k2];
xkkr = ar[j1][k2] - ar[k1][k2];
xkki = ai[j1][k2] - ai[k1][k2];
ar[j1][j2] = xjjr + xjkr;
ai[j1][j2] = xjji + xjki;
xr = xjjr - xjkr;
xi = xjji - xjki;
ar[j1][k2] = w2r * xr - w2i * xi;
ai[j1][k2] = w2r * xi + w2i * xr;
xr = xkjr + xkkr;
xi = xkji + xkki;
ar[k1][j2] = w1r * xr - w1i * xi;
ai[k1][j2] = w1r * xi + w1i * xr;
xr = xkjr - xkkr;
xi = xkji - xkki;
ar[k1][k2] = w12r * xr - w12i * xi;
ai[k1][k2] = w12r * xi + w12i * xr;
}
}
}
}
theta *= 2;
}
/* ---- unscrambler ---- */
i1 = 0;
for (j1 = 1; j1 < n - 1; j1++) {
for (k1 = n >> 1; k1 > (i1 ^= k1); k1 >>= 1);
if (j1 < i1) {
for (j2 = 0; j2 < n; j2++) {
xr = ar[j1][j2];
xi = ai[j1][j2];
ar[j1][j2] = ar[i1][j2];
ai[j1][j2] = ai[i1][j2];
ar[i1][j2] = xr;
ai[i1][j2] = xi;
}
}
}
for (j1 = 0; j1 < n; j1++) {
i2 = 0;
for (j2 = 1; j2 < n - 1; j2++) {
for (k2 = n >> 1; k2 > (i2 ^= k2); k2 >>= 1);
if (j2 < i2) {
xr = ar[j1][j2];
xi = ai[j1][j2];
ar[j1][j2] = ar[j1][i2];
ai[j1][j2] = ai[j1][i2];
ar[j1][i2] = xr;
ai[j1][i2] = xi;
}
}
}
}
|
このルーチンの基数は 2 ですが,さらに基数を 4 にすると同じ基数の Row-Column FFT に比べて複素数乗算回数は 5/8 に減ります.ただし, バタフライのループはとてつもなく巨大になります.実用の多次元 FFT ルーチンでの実行時間は,演算量よりもメモリーアクセスに強く 依存します.したがって,実際の応用ではあまり演算量にこだわらずに, メモリーアクセスを連続にするなどの工夫をする方がよいかもしれません.
この Vector-Radix FFT はさらに実数データの FFT や離散コサイン変換 などにも適用できます.