Next: Bibliography
Up: Schröder Triangles, Paths, and
Previous: 6. Generating function considerations
7. An algorithm for a product of zebras
We conclude with an algorithm for forming a product of two zebras, which provides
a combinatorial interpretation of the convolution related to
S(k)(x) = S(j-1)(x)S(k-j)(x),
or equivalently,
sk+1(x) = sj(x) sk-j+1(x),
for
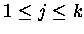 (
S(j)(x) is defined in
Subsection 6.2).
With S[k] denoting
(
S(j)(x) is defined in
Subsection 6.2).
With S[k] denoting
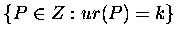 ,
our interpretation will involve defining a bijection
,
our interpretation will involve defining a bijection
Figure 6:
The first 3 steps of the algorithm.
 |
For fixed j and k,
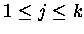 ,
the following algorithm, which
we will see is
invertible, produces a zebra
,
the following algorithm, which
we will see is
invertible, produces a zebra
![$P_3 \in {
S}^{[k]}$](img106.gif) for each
for each
![$ ( P_1, P_2 ) \in {S}^{[j-1]} \times {
S}^{[k-j]}$](img107.gif) :
:
- 1.
- We decompose P1 into two parts: the polyomino lying under the top row,
denoted by B1 and the remaining one, denoted by A1 (see
fig. 6 (a));
- 2.
- We construct the polyomino P3'''(which need not be "parallelogram") by attaching the polyomino P2 to A1 so the lower left cell of P2 takes the previous
position of the
lower left cell of B1.
(see fig. 6 (b));
- 3.
- We compose P3''' and B1, obtaining P3'',
by attaching the lower left cell of B1 beside the rightmost top cell
of P3''' (see fig. 6 (c));
- 4.
- We attach a column of length one less than that of the first column of B1above each
column of P2, contained in P3'', to obtain P3' (see fig. 6 (d)).
- 5.
- Finally, we obtain
the product
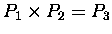 from P3' by:
from P3' by:
-
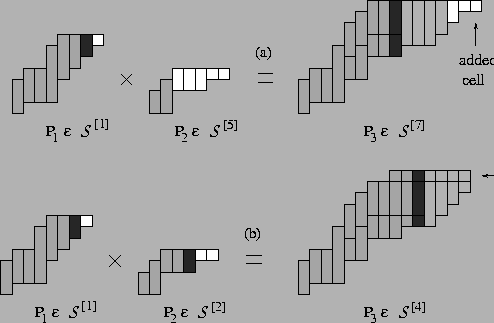
appending a white cell to the right of the top row of P3' if the
top row of P2
is completely white (see fig. 7 (a));
-
placing a new row at the top of P3' if the top row of P2 is not
completely white. It begins above
the rightmost black column of P2 and ends above the right column of
B1 (see fig. 7 (b));
- coloring the k rightmost columns of the resulting
polyomino white, in either case.
The remaining columns intersecting the top row of this polyomino take the same pattern of colors of the columns to the left of the
(j-1) rightmost consecutive white columns of B1.
Figure 7:
The product of P1 and P2.
 |
Given j and k, this construction can be easily reversed by first identifying the part
belonging
to B1 and then using the following observation to identify the
part belonging to A1.
If LA, LB, and Lmin denote, respectively,
the lengths of the right column of A1, the left column of B1, and
minimum length of all the columns P'3 that
intersect P2,
then
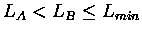 .
.
Next: Bibliography
Up: Schröder Triangles, Paths, and
Previous: 6. Generating function considerations
![]() ,
the following algorithm, which
we will see is
invertible, produces a zebra
,
the following algorithm, which
we will see is
invertible, produces a zebra
![]() for each
for each
![]() :
:
![]() .
.