 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.4.3 |
 |
Journal of Integer Sequences, Vol. 12 (2009), Article 09.4.3 |
Abstract:
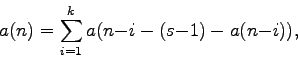
(Concerned with sequences A001511 A002572 A004128 A006949 A045412 A046699 A053735 A079559 A091090 A096346 A101925 A120501 A120502 A120503 A120504 A120505 A120506 A120507 A120508 A120509 A120510 A120511 A120512 A120513 A120514 A120515 A120516 A120517 A120518 A120519 A120520 A120521 A120522 A120523 A120524 A120525 A120526 A120527 A120528 A120529 A120530 A120531 and A120532.)
Received March 24 2009; revised version received May 1 2009. Published in Journal of Integer Sequences, May 12 2009.