 |
Journal of Integer Sequences, Vol. 14 (2011), Article 11.5.8 |
 |
Journal of Integer Sequences, Vol. 14 (2011), Article 11.5.8 |
Abstract:
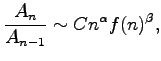
We also obtain some results on the Bell numbers ![]() using well-known formulae.
We compare the Bell numbers with
using well-known formulae.
We compare the Bell numbers with ![]()
![]() and
and ![]()
![]() .
.
Finally, applying the general statements proved in the article we obtain the formula
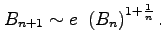
(Concerned with sequence
A000110.)
Received December 9 2010; revised version received March 28 2011; May 4 2011. Published in Journal of Integer Sequences, May 10 2011.