3.5 Falle and Komissarov upwind scheme
Instead of starting from the conservative form of the hydrodynamic equations, one can use a primitive
variable formulation in quasi-linear form,
where 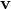 is any set of primitive variables. A local linearization of the above system allows one to obtain
the solution of the Riemann problem, and from this the numerical fluxes needed to advance a conserved
version of the equations in time.
is any set of primitive variables. A local linearization of the above system allows one to obtain
the solution of the Riemann problem, and from this the numerical fluxes needed to advance a conserved
version of the equations in time.
Falle and Komissarov [89 ] have considered two different algorithms to solve the local Riemann problems
in SRHD by extending the methods devised in [87]. In a first algorithm, the intermediate states of the
Riemann problem at both sides of the contact discontinuity,
] have considered two different algorithms to solve the local Riemann problems
in SRHD by extending the methods devised in [87]. In a first algorithm, the intermediate states of the
Riemann problem at both sides of the contact discontinuity, 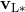 and
and 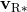 , are obtained by solving the
system
, are obtained by solving the
system
where 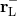 is the right eigenvector of
is the right eigenvector of 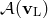 associated with sound waves moving upstream, and
associated with sound waves moving upstream, and 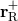 is
the right eigenvector of
is
the right eigenvector of 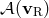 of sound waves moving downstream. The continuity of pressure and of the
normal component of the velocity across the contact discontinuity allows one to obtain the wave strengths
of sound waves moving downstream. The continuity of pressure and of the
normal component of the velocity across the contact discontinuity allows one to obtain the wave strengths
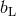 and
and 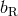 from the above expressions, and hence the linear approximation to the intermediate state
from the above expressions, and hence the linear approximation to the intermediate state
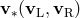 .
.
In the second algorithm proposed by Falle and Komissarov [89 ], a linearization of system (41) is
obtained by constructing a constant matrix
], a linearization of system (41) is
obtained by constructing a constant matrix 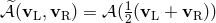 . The solution of the
corresponding Riemann problem is that of a linear system with matrix
. The solution of the
corresponding Riemann problem is that of a linear system with matrix 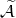 , i.e.,
, i.e.,
or, equivalently,
with
where 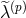 ,
, 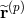 , and
, and 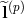 are the eigenvalues and the right and left eigenvectors of
are the eigenvalues and the right and left eigenvectors of 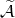 , respectively (p
runs from 1 to the number of equations of the system).
, respectively (p
runs from 1 to the number of equations of the system).
In both algorithms, the final step involves the computation of the numerical fluxes for the conservation
equations,
![]() ] have considered two different algorithms to solve the local Riemann problems
in SRHD by extending the methods devised in [87]. In a first algorithm, the intermediate states of the
Riemann problem at both sides of the contact discontinuity,
] have considered two different algorithms to solve the local Riemann problems
in SRHD by extending the methods devised in [87]. In a first algorithm, the intermediate states of the
Riemann problem at both sides of the contact discontinuity, ![]() and
and ![]() , are obtained by solving the
system
, are obtained by solving the
system ![]() ], a linearization of system (41
], a linearization of system (41![]() ) is
obtained by constructing a constant matrix
) is
obtained by constructing a constant matrix ![]() . The solution of the
corresponding Riemann problem is that of a linear system with matrix
. The solution of the
corresponding Riemann problem is that of a linear system with matrix ![]() , i.e.,
, i.e.,