9.3 Spectral decomposition of the 3D SRHD equations
The full spectral decomposition including the right and left eigenvectors of the Jacobian matrices
associated to the SRHD system in 3D has been first derived by Donat et al. [75]. Previously, Martí
et al. [179] obtained the spectral decomposition in 1D SRHD, and Eulderink [83] and Font
et al. [92] derived the eigenvalues and right eigenvectors in 3D. The Jacobians are given by
where the state vector 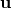 and the flux vector
and the flux vector 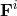 are defined in Equations (6) and (7), respectively. In
the following we explicitly give both the eigenvalues and the right and left eigenvectors of the Jacobi matrix
are defined in Equations (6) and (7), respectively. In
the following we explicitly give both the eigenvalues and the right and left eigenvectors of the Jacobi matrix
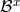 only (the cases i = y, z are easily obtained by symmetry considerations).
only (the cases i = y, z are easily obtained by symmetry considerations).
The eigenvalues of matrix 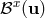 are
are
and
A complete set of right-eigenvectors is
where
The corresponding complete set of left-eigenvectors is
where 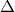 is the determinant of the matrix of right-eigenvectors, i.e.,
For an ideal gas equation of state
is the determinant of the matrix of right-eigenvectors, i.e.,
For an ideal gas equation of state 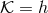 , i.e.,
, i.e., 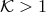 , and hence
, and hence 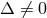 for
for 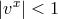 .
.
![]() are
are