2.1 Equations
Using the Einstein summation convention the equations describing the motion of a relativistic fluid are
given by the five conservation laws,
where 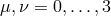 , and where
, and where 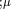 denotes the covariant derivative with respect to coordinate
denotes the covariant derivative with respect to coordinate 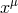 .
Furthermore,
.
Furthermore, 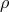 is the proper rest mass density of the fluid,
is the proper rest mass density of the fluid, 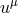 its four-velocity, and
its four-velocity, and 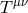 is the
stress-energy tensor, which for a perfect fluid can be written as
Here,
is the
stress-energy tensor, which for a perfect fluid can be written as
Here, 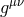 is the metric tensor,
is the metric tensor, 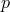 the fluid pressure, and
the fluid pressure, and 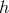 the specific enthalpy of the fluid defined by
where
the specific enthalpy of the fluid defined by
where  is the specific internal energy. Note that we use natural units (i.e., the speed of light c = 1)
throughout this review.
is the specific internal energy. Note that we use natural units (i.e., the speed of light c = 1)
throughout this review.
In Minkowski spacetime and Cartesian coordinates 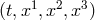 , the conservation equations (1, 2) can
be written in vector form as
, the conservation equations (1, 2) can
be written in vector form as
where i = 1 ,2 ,3. The state vector 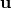 is defined by
and the flux vectors
is defined by
and the flux vectors 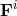 are given by
The five conserved quantities
are given by
The five conserved quantities 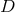 ,
, 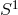 ,
, 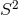 ,
, 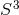 , and
, and 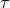 are the rest mass density, the three
components of the momentum density, and the energy density (measured relative to the rest mass energy
density), respectively. They are all measured in the laboratory frame, and are related to quantities in the
local rest frame of the fluid (primitive variables) through
where
are the rest mass density, the three
components of the momentum density, and the energy density (measured relative to the rest mass energy
density), respectively. They are all measured in the laboratory frame, and are related to quantities in the
local rest frame of the fluid (primitive variables) through
where 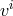 are the components of the three-velocity of the fluid
and
are the components of the three-velocity of the fluid
and 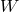 is the Lorentz factor,
The system of Equations (5) with Definitions (6, 7, 8, 9, 10, 11, 12) is closed by means of an equation of
state (EOS), which we shall assume to be given in the form
is the Lorentz factor,
The system of Equations (5) with Definitions (6, 7, 8, 9, 10, 11, 12) is closed by means of an equation of
state (EOS), which we shall assume to be given in the form
In the non-relativistic limit (i.e., 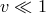 ,
, 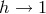 )
) 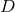 ,
, 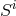 , and
, and 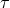 approach their Newtonian
counterparts
approach their Newtonian
counterparts 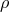 ,
, 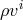 , and
, and 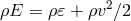 , and Equations (5) reduce to the classical ones. In the
relativistic case the equations of system (5) are strongly coupled via the Lorentz factor and the specific
enthalpy, which gives rise to numerical complications (see Section 2.3).
, and Equations (5) reduce to the classical ones. In the
relativistic case the equations of system (5) are strongly coupled via the Lorentz factor and the specific
enthalpy, which gives rise to numerical complications (see Section 2.3).
In classical numerical hydrodynamics it is very easy to obtain 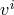 from the conserved quantities (i.e.,
from the conserved quantities (i.e.,
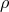 and
and 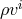 ). In the relativistic case, however, the task to recover
). In the relativistic case, however, the task to recover 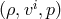 from
from 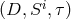 is much
more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the
conserved quantities are advanced in time, it is necessary to compute the primitive variables from the
conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial
ingredient of any algorithm (see Section 9.2).
is much
more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the
conserved quantities are advanced in time, it is necessary to compute the primitive variables from the
conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial
ingredient of any algorithm (see Section 9.2).
![]() , the conservation equations (1
, the conservation equations (1![]() , 2
, 2![]() ) can
be written in vector form as
) can
be written in vector form as ![]() ,
, ![]() )
) ![]() ,
, ![]() , and
, and ![]() approach their Newtonian
counterparts
approach their Newtonian
counterparts ![]() ,
, ![]() , and
, and ![]() , and Equations (5
, and Equations (5![]() ) reduce to the classical ones. In the
relativistic case the equations of system (5
) reduce to the classical ones. In the
relativistic case the equations of system (5![]() ) are strongly coupled via the Lorentz factor and the specific
enthalpy, which gives rise to numerical complications (see Section 2.3).
) are strongly coupled via the Lorentz factor and the specific
enthalpy, which gives rise to numerical complications (see Section 2.3).
![]() from the conserved quantities (i.e.,
from the conserved quantities (i.e.,
![]() and
and ![]() ). In the relativistic case, however, the task to recover
). In the relativistic case, however, the task to recover ![]() from
from ![]() is much
more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the
conserved quantities are advanced in time, it is necessary to compute the primitive variables from the
conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial
ingredient of any algorithm (see Section 9.2).
is much
more complicated. Moreover, as state-of-the-art SRHD codes are based on conservative schemes where the
conserved quantities are advanced in time, it is necessary to compute the primitive variables from the
conserved ones one (or even several) times per numerical cell and time step making this procedure a crucial
ingredient of any algorithm (see Section 9.2).