2.3 Parallel propagator
2.3.1 Tetrad on 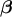
On the geodesic 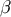 that links
that links 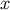 to
to 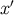 we introduce an orthonormal basis
we introduce an orthonormal basis 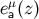 that is parallel transported on the geodesic.
The frame indices
that is parallel transported on the geodesic.
The frame indices
 ,
,  , …, run from 0 to 3, and the frame vectors satisfy
, …, run from 0 to 3, and the frame vectors satisfy
where 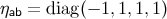 is the Minkowski metric (which we shall use to raise and lower frame
indices). We have the completeness relations
and we define a dual tetrad
is the Minkowski metric (which we shall use to raise and lower frame
indices). We have the completeness relations
and we define a dual tetrad 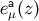 by
this is also parallel transported on
by
this is also parallel transported on 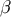 . In terms of the dual tetrad the completeness relations take the form
and it is easy to show that the tetrad and its dual satisfy
. In terms of the dual tetrad the completeness relations take the form
and it is easy to show that the tetrad and its dual satisfy 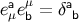 and
and 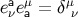 . Equations (68, 69,
70, 71) hold everywhere on
. Equations (68, 69,
70, 71) hold everywhere on 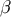 . In particular, with an appropriate change of notation they hold at
. In particular, with an appropriate change of notation they hold at 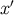 and
and
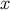 ; for example,
; for example, 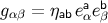 is the metric at
is the metric at 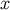 .
.
2.3.2 Definition and properties of the parallel propagator
Any vector field 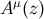 on
on 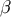 can be decomposed in the basis
can be decomposed in the basis 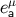 :
: 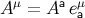 , and the vector’s frame
components are given by
, and the vector’s frame
components are given by 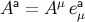 . If
. If 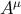 is parallel transported on the geodesic, then the
coefficients
is parallel transported on the geodesic, then the
coefficients 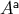 are constants. The vector at
are constants. The vector at 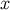 can then be expressed as
can then be expressed as 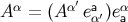 , or
, or
The object 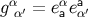 is the parallel propagator: It takes a vector at
is the parallel propagator: It takes a vector at 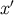 and parallel-transports it to
and parallel-transports it to
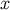 along the unique geodesic that links these points.
along the unique geodesic that links these points.
Similarly, we find that
and we see that 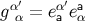 performs the inverse operation: It takes a vector at
performs the inverse operation: It takes a vector at 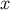 and
parallel-transports it back to
and
parallel-transports it back to 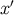 . Clearly,
and these relations formally express the fact that
. Clearly,
and these relations formally express the fact that 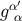 is the inverse of
is the inverse of 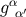 .
.
The relation 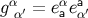 can also be expressed as
can also be expressed as  , and this reveals that
, and this reveals that
The ordering of the indices, and the ordering of the arguments, are therefore arbitrary.
The action of the parallel propagator on tensors of arbitrary ranks is easy to figure out. For example,
suppose that the dual vector 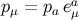 is parallel transported on
is parallel transported on 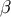 . Then the frame components
. Then the frame components
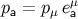 are constants, and the dual vector at
are constants, and the dual vector at 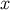 can be expressed as
can be expressed as 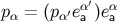 , or
, or
It is therefore the inverse propagator 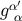 that takes a dual vector at
that takes a dual vector at 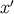 and parallel-transports it to
and parallel-transports it to  .
As another example, it is easy to show that a tensor
.
As another example, it is easy to show that a tensor 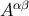 at
at 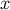 obtained by parallel transport from
obtained by parallel transport from 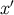 must be given by
Here we need two occurrences of the parallel propagator, one for each tensorial index. Because the metric
tensor is covariantly constant, it is automatically parallel transported on
must be given by
Here we need two occurrences of the parallel propagator, one for each tensorial index. Because the metric
tensor is covariantly constant, it is automatically parallel transported on 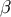 , and a special case of
Equation (77) is therefore
, and a special case of
Equation (77) is therefore 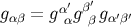 .
.
Because the basis vectors are parallel transported on 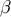 , they satisfy
, they satisfy 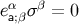 at
at 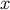 and
and 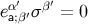 at
at 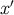 . This immediately implies that the parallel propagators must satisfy
. This immediately implies that the parallel propagators must satisfy
Another useful property of the parallel propagator follows from the fact that if 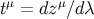 is tangent to
the geodesic connecting
is tangent to
the geodesic connecting 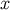 to
to 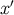 , then
, then 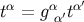 . Using Equations (55) and (56), this observation
gives us the relations
. Using Equations (55) and (56), this observation
gives us the relations
2.3.3 Coincidence limits
Equation (72) and the completeness relations of Equations (69) or (71) imply that
Other coincidence limits are obtained by differentiation of Equations (78). For example, the relation
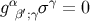 implies
implies 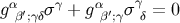 , and at coincidence we have
the second result was obtained by applying Synge’s rule on the first result. Further differentiation
gives
, and at coincidence we have
the second result was obtained by applying Synge’s rule on the first result. Further differentiation
gives
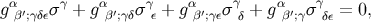
and at coincidence we have ![α α [g β′;γδ] + [gβ′;δγ] = 0](article767x.gif) , or
, or ![α α′ 2 [g β′;γδ] + R β′γ′δ′ = 0](article768x.gif) . The coincidence limit for
. The coincidence limit for
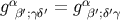 can then be obtained from Synge’s rule, and an additional application of the rule gives
can then be obtained from Synge’s rule, and an additional application of the rule gives
![[gαβ′;γ′δ′]](article770x.gif) . Our results are
. Our results are
![]() that links
that links ![]() to
to ![]() we introduce an orthonormal basis
we introduce an orthonormal basis ![]() that is parallel transported on the geodesic.
The frame indices3
that is parallel transported on the geodesic.
The frame indices3
![]() ,
, ![]() , …, run from 0 to 3, and the frame vectors satisfy
, …, run from 0 to 3, and the frame vectors satisfy ![]() on
on ![]() can be decomposed in the basis
can be decomposed in the basis ![]() :
: ![]() , and the vector’s frame
components are given by
, and the vector’s frame
components are given by ![]() . If
. If ![]() is parallel transported on the geodesic, then the
coefficients
is parallel transported on the geodesic, then the
coefficients ![]() are constants. The vector at
are constants. The vector at ![]() can then be expressed as
can then be expressed as ![]() , or
, or
![]() can also be expressed as
can also be expressed as ![]() , and this reveals that
, and this reveals that
![]() is parallel transported on
is parallel transported on ![]() . Then the frame components
. Then the frame components
![]() are constants, and the dual vector at
are constants, and the dual vector at ![]() can be expressed as
can be expressed as ![]() , or
, or
![]() , they satisfy
, they satisfy ![]() at
at ![]() and
and ![]() at
at ![]() . This immediately implies that the parallel propagators must satisfy
. This immediately implies that the parallel propagators must satisfy
![]() ) and the completeness relations of Equations (69
) and the completeness relations of Equations (69![]() ) or (71
) or (71![]() ) imply that
) imply that ![]() , or
, or ![]() . The coincidence limit for
. The coincidence limit for
![]() can then be obtained from Synge’s rule, and an additional application of the rule gives
can then be obtained from Synge’s rule, and an additional application of the rule gives
![]() . Our results are
. Our results are