Transformation between Fermi and retarded coordinates; advanced point

3.4 Transformation between Fermi and retarded coordinates; advanced point

A point $x$ in the normal convex neighbourhood of a world line $γ$ can be assigned a set of Fermi normal coordinates (as in Section 3.2), or it can be assigned a set of retarded coordinates (see Section 3.3). These coordinate systems can obviously be related to one another, and our first task in this section (which will occupy us in Sections 3.4.1, 3.4.2, and 3.4.3) will be to derive the transformation rules. We begin by refining our notation so as to eliminate any danger of ambiguity.

Figure 8:

The retarded, simultaneous, and advanced points on a world line $γ$ . The retarded point $′ x ≡ z(u)$ is linked to $x$ by a future-directed null geodesic. The simultaneous point $¯x ≡ z(t)$ is linked to $x$ by a spacelike geodesic that intersects $γ$ orthogonally. The advanced point $x′′ ≡ z(v)$ is linked to $x$ by a past-directed null geodesic.

The Fermi normal coordinates of $x$ refer to a point $¯x ≡ z(t)$ on $γ$ that is related to $x$ by a spacelike geodesic that intersects $γ$ orthogonally (see Figure 8 ). We refer to this point as $x$ ’s simultaneous point, and to tensors at $¯x$ we assign indices $¯α$ , $¯β$ , etc. We let $(t,sωa )$ be the Fermi normal coordinates of $x$ , with $t$ denoting the value of $γ$ ’s proper-time parameter at $¯x$ , $∘ -------- s = 2σ(x, ¯x)$ representing the proper distance from $¯x$ to $x$ along the spacelike geodesic, and $a ω$ denoting a unit vector ( $a b δabω ω = 1$ ) that determines the direction of the geodesic. The Fermi normal coordinates are defined by $sωa = − ea¯ασ ¯α$ and $σα¯u ¯α = 0$ . Finally, we denote by $(¯eα,¯eα) 0 a$ the tetrad at $x$ that is obtained by parallel transport of $(u¯α,eα¯) a$ on the spacelike geodesic.

The retarded coordinates of $x$ refer to a point $′ x ≡ z (u )$ on $γ$ that is linked to $x$ by a future-directed null geodesic (see Figure 8 ). We refer to this point as $x$ ’s retarded point, and to tensors at $x ′$ we assign indices $α ′$ , $β′$ , etc. We let $(u,rΩa)$ be the retarded coordinates of $x$ , with $u$ denoting the value of $γ$ ’s proper-time parameter at $x′$ , $r = σ ′u α′ α$ representing the affine-parameter distance from $′ x$ to $x$ along the null geodesic, and $a Ω$ denoting a unit vector ( $a b δabΩ Ω = 1$ ) that determines the direction of the geodesic. The retarded coordinates are defined by $a a α′ rΩ = − eα′σ$ and $σ (x, x′) = 0$ . Finally, we denote by $(eα0,eαa)$ the tetrad at $x$ that is obtained by parallel transport of $(uα′,eαa′)$ on the null geodesic.

The reader not interested in following the details of this discussion can be informed that

our results concerning the transformation from the retarded coordinates $(u,r,Ωa )$ to the Fermi normal coordinates $(t,s,ωa )$ are contained in Equations (218 , 219 , 220 ) below;
our results concerning the transformation from the Fermi normal coordinates $(t,s,ωa)$ to the retarded coordinates $(u,r,Ωa)$ are contained in Equations (221 , 222 , 223 );
the decomposition of each member of $α α (¯e0,¯ea)$ in the tetrad $α α (e0,ea)$ is given in retarded coordinates by Equations (224 ) and (225 ); and
the decomposition of each member of $(eα,eα) 0 a$ in the tetrad $(¯eα,¯eα) 0 a$ is given in Fermi normal coordinates by Equations (226 ) and (227 ).

Our final task will be to define, along with the retarded and simultaneous points, an advanced point $x ′′$ on the world line $γ$ (see Figure 8 ). This is taken on in Section 3.4.4. Throughout this section we shall set $ωab = 0$ , where $ωab$ is the rotation tensor defined by Equation (138 ) – the tetrad vectors $eμ a$ will be assumed to be Fermi–Walker transported on $γ$ .

3.4.1 From retarded to Fermi coordinates

Quantities at $¯x ≡ z(t)$ can be related to quantities at $x′ ≡ z(u)$ by Taylor expansion along the world line $γ$ . To implement this strategy we must first find an expression for $Δ ≡ t − u$ . (Although we use the same notation, this should not be confused with the van Vleck determinant introduced in Section 2.5.)

Consider the function $p(τ)$ of the proper-time parameter $τ$ defined by

μ p(τ) = σμ(x,z (τ ))u (τ),

in which $x$ is kept fixed and in which $z (τ)$ is an arbitrary point on the world line. We have that $p(u ) = r$ and $p(t) = 0$ , and $Δ$ can ultimately be obtained by expressing $p(t)$ as $p(u + Δ)$ and expanding in powers of $Δ$ . Formally,

1 1 p(t) = p(u ) + p˙(u)Δ + --¨p(u)Δ2 + --p(3)(u)Δ3 + 𝒪 (Δ4 ), 2 6

where overdots (or a number within brackets) indicate repeated differentiation with respect to $τ$ . We have

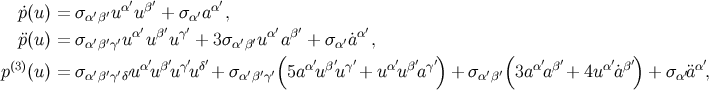
α′ β′ α′ p˙(u ) = σα′β′u u′ +′ σ′α′a , ′ ′ ′ p¨(u ) = σα′β′γ′u αu βuγ + 3σα′β′u αaβ + σα′˙aα , (3) α′β′ γ′δ′ ( α′ β′γ′ α′β′γ′) ( α′β′ α′β′) α′ p (u ) = σα′β′γ′δ′u u u u + σα′β′γ′ 5a u u + u u a + σα′β′ 3a a + 4u ˙a + σ α′¨a ,

where $aμ = Du μ∕d τ$ , $a˙μ = Da μ∕dτ$ , and $¨aμ = D a˙μ∕dτ$ .

We now express all of this in retarded coordinates by invoking the expansion of Equation (88 ) for $σα′β′$ (as well as additional expansions for the higher derivatives of the world function, obtained by further differentiation of this result) and the relation $′ ′ ′ σ α = − r(uα + Ωaeαa )$ first derived in Equation (144 ). With a degree of accuracy sufficient for our purposes we obtain

[ ] a 1- 2 3 p˙(u ) = − 1 + raaΩ + 3 r S + 𝒪 (r ) , a 2 ¨p(u ) = − r (˙a0 + a˙aΩ ) + 𝒪 (r ), p(3)(u ) = a˙0 + 𝒪 (r),

where $a b S = Ra0b0Ω Ω$ was first introduced in Equation (162

), and where $α′ ˙a0 ≡ ˙aα′u$ , $α′ a˙a ≡ ˙aα′ea$ are the frame components of the covariant derivative of the acceleration vector. To arrive at these results we made use of the identity $′ ′ aα′a α + ˙aα′uα = 0$ that follows from the fact that $aμ$ is orthogonal to $uμ$ . Notice that there is no distinction between the two possible interpretations $˙aa ≡ daa ∕dτ$ and $a˙a ≡ ˙aμeμ a$ for the quantity $a˙a (τ )$ ; their equality follows at once from the substitution of $μ μ De a∕dτ = aau$ (which states that the basis vectors are Fermi–Walker transported on the world line) into the identity $daa ∕dτ = D (aνeνa)∕dτ$ .

Collecting our results we obtain

[ ] a 1- 2 3 1- a 2 1- 3 4 r = 1 + raaΩ + 3 r S + 𝒪 (r ) Δ + 2r [˙a0 + a˙aΩ + 𝒪 (r)]Δ − 6 [˙a0 + 𝒪 (r)]Δ + 𝒪 (Δ ),

which can readily be solved for $Δ ≡ t − u$ expressed as an expansion in powers of $r$ . The final result is

{ } t = u + r 1− raa(u)Ωa + r2 [aa(u)Ωa ]2− 1r2a˙0(u ) − 1r2˙aa(u)Ωa − 1-r2Ra0b0(u )ΩaΩb + 𝒪 (r3) , 3 2 3 (218 )

where we show explicitly that all frame components are evaluated at the retarded point $z(u)$ .

To obtain relations between the spatial coordinates we consider the functions

pa(τ) = − σμ (x,z(τ))eμ(τ ), a

in which $x$ is fixed and $z (τ )$ is an arbitrary point on $γ$ . We have that the retarded coordinates are given by $rΩa = pa(u)$ , while the Fermi coordinates are given instead by $sωa = pa(t) = pa(u + Δ )$ . This last expression can be expanded in powers of $Δ$ , producing

a a a 1- a 2 1- a(3) 3 4 sω = p (u ) + p˙(u)Δ + 2 ¨p (u )Δ + 6 p (u)Δ + 𝒪 (Δ ),

with

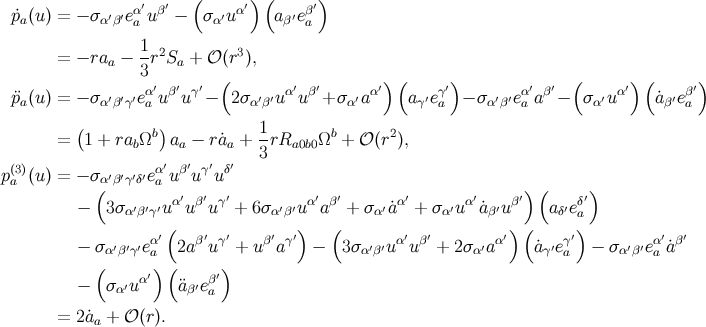
( ) ( ) p˙(u ) = − σ ′′eα′u β′ − σ ′u α′ a ′eβ′ a αβ a α β a 1 2 3 = − raa − 3-r Sa + 𝒪 (r ), ′ ′ ′ ( ′ ′ ′) ( ′) ′ ′ ( ′) ( ′) p¨a(u ) = − σ α′β′γ′eαa uβ uγ − 2σα′β′u αu β+ σα ′aα aγ′eγa − σα′β′eαa aβ − σα′uα ˙aβ′eβa ( ) = 1 + rabΩb aa − ra˙a + 1-rRa0b0Ωb + 𝒪 (r2), 3 p(a3)(u ) = − σ α′β′γ′δ′eαa′uβ′uγ′uδ′ ( ′ ′ ′ ′ ′ ′ ′ ′)( ′) − 3σ α′β′γ′u αuβ uγ + 6σα′β′uα aβ + σα′˙aα + σα′uα ˙aβ′uβ aδ′eδa ′( ′ ′ ′ ′) ( ′ ′ ′)( ′) ′ ′ − σα′β′γ′eαa 2aβ uγ + uβ aγ − 3σα′β′u αuβ + 2σα′aα ˙aγ′eγa − σ α′β′eαaa˙β ( ) ( ) − σ α′uα′ ¨aβ′eβa′ = 2 ˙aa + 𝒪 (r).

To arrive at these results we have used the same expansions as before and re-introduced $b b c Sa = Ra0b0Ω − Rab0cΩ Ω$ , as it was first defined in Equation (161

Collecting our results we obtain

[ ] [ ] sωa = rΩa − r aa + 1rSa + 𝒪 (r2) Δ + 1- (1 + ra Ωb)aa − ra˙a + 1rRa Ωb + 𝒪 (r2) Δ2 3 2 b 3 0b0 1 + --[˙aa + 𝒪 (r)]Δ3 + 𝒪 (Δ4), 3

which becomes

{ 1 [ ] 1 1 1 } sωa = r Ωa − -r 1− rab(u)Ωb aa(u) − -r2˙aa(u) − --r2Ra0b0(u)Ωb + --r2Rab0c(u )Ωb Ωc+ 𝒪 (r3) 2 6 6 3 (219 )

after substituting Equation (218

) for $Δ ≡ t − u$ . From squaring Equation (219

) and using the identity $a b δabω ω = 1$ we can also deduce

{ 1 3 1 1 1 } s = r 1 − -raa(u)Ωa + -r2[aa(u)Ωa ]2 − --r2˙a0(u) − -r2˙aa(u)Ωa − -r2Ra0b0(u)Ωa Ωb + 𝒪 (r3) 2 8 8 6 6 (220 )

for the spatial distance between $x$ and $z(t)$ .

3.4.2 From Fermi to retarded coordinates

The techniques developed in the preceding Section 3.4.2 can easily be adapted to the task of relating the retarded coordinates of $x$ to its Fermi normal coordinates. Here we use $¯x ≡ z(t)$ as the reference point and express all quantities at $′ x ≡ z(u)$ as Taylor expansions about $τ = t$ .

We begin by considering the function

σ(τ ) = σ (x,z(τ ))

of the proper-time parameter $τ$ on $γ$ . We have that $σ (t) = 1s2 2$ and $σ(u) = 0$ , and $Δ ≡ t − u$ is now obtained by expressing $σ(u)$ as $σ(t − Δ )$ and expanding in powers of $Δ$ . Using the fact that $σ˙(τ ) = p(τ)$ , we have

1- 2 1- 3 -1- (3) 4 5 σ(u ) = σ(t) − p(t)Δ + 2p˙(t)Δ − 6¨p(t)Δ + 24 p (t)Δ + 𝒪 (Δ ).

Expressions for the derivatives of $p(τ )$ evaluated at $τ = t$ can be constructed from results derived previously in Section 3.4.1: it suffices to replace all primed indices by barred indices and then substitute the relation $¯α a ¯α σ = − sω ea$ that follows immediately from Equation (116 ). This gives

[ 1 ] ˙p(t) = − 1 + saa ωa +-s2Ra0b0ωa ωb + 𝒪 (s3) , 3 ¨p(t) = − s˙aaωa + 𝒪 (s2), (3) p (t) = ˙a0 + 𝒪 (s),

and then

[ ] s2 = 1 + sa ωa + 1s2R ωa ωb+ 𝒪 (s3) Δ2 − 1-s[˙a ωa + 𝒪 (s)]Δ3 − -1-[˙a + 𝒪(s)]Δ4 + 𝒪 (Δ5 ) a 3 a0b0 3 a 12 0

after recalling that $p(t) = 0$ . Solving for $Δ$ as an expansion in powers of $s$ returns

{ } u = t − s 1 − 1saa(t)ωa + 3s2 [aa (t)ωa]2+ 1-s2˙a0(t) + 1s2˙aa(t)ωa− 1s2Ra0b0(t)ωaωb+ 𝒪(s3) , 2 8 24 6 6 (221 )

in which we emphasize that all frame components are evaluated at the simultaneous point $z(t)$ .

An expression for $r = p(u)$ can be obtained by expanding $p(t − Δ )$ in powers of $Δ$ . We have

1 2 1 (3) 3 4 r = − ˙p(t)Δ + -¨p(t)Δ − --p (t)Δ + 𝒪 (Δ ), 2 6

and substitution of our previous results gives

{ } 1- a 1-2 a 2 1-2 1-2 a 1-2 a b 3 r = s 1 + 2saa (t)ω − 8s [aa(t)ω ] − 8s ˙a0(t) − 3s ˙aa(t)ω + 6s Ra0b0(t)ω ω + 𝒪 (s ) (222 )

for the retarded distance between $x$ and $z (u )$ .

Finally, the retarded coordinates $a a rΩ = p (u)$ can be related to the Fermi coordinates by expanding $a p (t − Δ )$ in powers of $Δ$ , so that

a a a 1- a 2 1-a(3) 3 4 rΩ = p (t) − ˙p (t)Δ + 2 ¨p (t)Δ − 6p (t)Δ + 𝒪(Δ ).

Results from the preceding Section 3.4.2 can again be imported with mild alterations, and we find

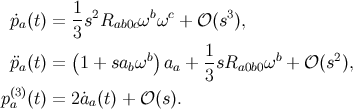
˙pa(t) = 1-s2Rab0cωbωc + 𝒪 (s3), 3 ( b) 1- b 2 ¨pa(t) = 1 + sabω aa + 3sRa0b0ω + 𝒪 (s ), p(3)(t) = 2a˙(t) + 𝒪 (s). a a

This, together with Equation (221

), gives

It may be checked that squaring this equation and using the identity $δabΩaΩb = 1$ returns the same result as Equation (222

3.4.3 Transformation of the tetrads at $x$

Recall that we have constructed two sets of basis vectors at $x$ . The first set is the tetrad $(¯eα,¯eα) 0 a$ that is obtained by parallel transport of $(u¯α,e¯α) a$ on the spacelike geodesic that links $x$ to the simultaneous point $¯x ≡ z (t)$ . The second set is the tetrad $α α (e0 ,ea)$ that is obtained by parallel transport of $α′ α′ (u ,ea )$ on the null geodesic that links $x$ to the retarded point $x′ ≡ z(u)$ . Since each tetrad forms a complete set of basis vectors, each member of $(e¯α0,¯eαa)$ can be decomposed in the tetrad $(eα0,eαa)$ , and correspondingly, each member of $(eα,eα) 0 a$ can be decomposed in the tetrad $(¯eα,¯eα) 0 a$ . These decompositions are worked out in this Section. For this purpose we shall consider the functions

p α(τ) = gαμ (x,z(τ))u μ(τ), pαa(τ ) = g αμ (x,z(τ))eμa(τ),

in which $x$ is a fixed point in a neighbourhood of $γ$ , $z(τ)$ is an arbitrary point on the world line, and $α g μ(x,z)$ is the parallel propagator on the unique geodesic that links $x$ to $z$ . We have $α α ¯e0 = p (t)$ , $¯eαa = p αa(t)$ , $eα0 = pα(u)$ , and $eαa = p αa(u)$ .

We begin with the decomposition of $(¯eα ,¯eα) 0 a$ in the tetrad $(eα ,eα) 0 a$ associated with the retarded point $z(u )$ . This decomposition will be expressed in the retarded coordinates as an expansion in powers of $r$ . As in Section 3.2.1 we express quantities at $z(t)$ in terms of quantities at $z(u)$ by expanding in powers of $Δ ≡ t − u$ . We have

α α α 1-α 2 3 ¯e0 = p (u) + ˙p (u)Δ + 2¨p (u)Δ + 𝒪 (Δ ),

with

˙pα(u) = gα uα′uβ′ + gα aα′ [ α′;β′ α′ ] a 1- a b 2 α = a + 2rR 0b0Ω + 𝒪 (r ) ea, ′ ′ ′ ( ′ ′ ′ ′) ′ ¨pα(u) = gαα′;β′γ′uα uβ uγ + g αα′;β′ 2aα uβ + uα aβ + gαα′a˙α α a α = [− ˙a0 + 𝒪 (r)]e0 + [˙a + 𝒪 (r)]ea ,

where we have used the expansions of Equation (92

) as well as the decompositions of Equation (141

). Collecting these results and substituting Equation (218

) for $Δ$ yields

[ ] [ ( ) ] e¯α0 = 1− 1r2˙a0(u) + 𝒪 (r3) eα0 + r 1− abΩb aa(u) + 1r2a˙a (u ) + 1r2Ra0b0(u)Ωb + 𝒪 (r3) eαa. 2 2 2 (224 )

Similarly, we have

α α α 1 α 2 3 ¯ea = pa(u) + ˙pa(u)Δ + -¨pa(u)Δ + 𝒪 (Δ ), 2

with

( ) ( ) p˙α(u ) = g α eα′uβ′ + gα uα′ a ′eβ′ a α′;β′ a α′ β a [ 1 ] [ 1 ] = aa + -rRa0b0Ωb + 𝒪 (r2) eα0 + − -rRba0cΩc + 𝒪 (r2) eαb , 2 ( 2 ) ( )( ) ( )( ) ¨pα(u ) = g α′ ′ ′eα′uβ′u γ′+ gα ′′ 2uα ′uβ′a ′eγ′+ eα′aβ′ + g α′aα′ a ′eβ′ + gα ′uα′ ˙a ′eβ′ a α ;β γ a [ α ;β ] γ a a α β a α β a = [˙aa + 𝒪 (r)]eα0 + aaab + 𝒪 (r) eαb ,

and all this gives

[ 1 1 ] e¯αa = δba +--r2ab(u)aa(u) − -r2Rba0c(u)Ωc + 𝒪 (r3) eαb [ 2 2 ] ( b) 1 2 1 2 b 3 α + r 1 − rabΩ aa (u ) + -r ˙aa(u) + -r Ra0b0(u)Ω + 𝒪(r ) e0. (225 ) 2 2

We now turn to the decomposition of $(eα,eα) 0 a$ in the tetrad $(¯eα,¯eα) 0 a$ associated with the simultaneous point $z(t)$ . This decomposition will be expressed in the Fermi normal coordinates as an expansion in powers of $s$ . Here, as in Section 3.2.2, we shall express quantities at $z(u)$ in terms of quantities at $z(t)$ . We begin with

eα = pα (t) − ˙pα(t)Δ + 1¨pα(t)Δ2 + 𝒪 (Δ3 ), 0 2

and we evaluate the derivatives of $pα(τ)$ at $τ = t$ . To accomplish this we rely on our previous results (replacing primed indices with barred indices), on the expansions of Equation (92 ), and on the decomposition of $α gα¯(x, ¯x)$ in the tetrads at $x$ and $¯x$ . This gives

[ ] ˙pα(t) = aa + 1sRa ωb + 𝒪 (s2) ¯eα , 2 0b0 a ¨pα(t) = [− ˙a0 + 𝒪 (s)]¯eα+ [˙aa + 𝒪 (s)]¯eα, 0 a

and we finally obtain

[ ] [ ( ) ] α 1 2 3 α 1 b a 1 2 a 1 2 a b 3 α e0 = 1− --s ˙a0(t) + 𝒪 (s ) ¯e0+ − s 1− -sab ω a (t) + -s ˙a (t) − -s R 0b0(t)ω + 𝒪 (s ) ¯ea. 2 2 2 2 (226 )

Similarly, we write

α α α 1-α 2 3 ea = pa (t) − ˙pa(t)Δ + 2¨pa(t)Δ + 𝒪 (Δ ),

in which we substitute

[ ] [ ] α 1 b 2 α 1 b c 2 α p˙a(t) = aa + 2sRa0b0ω + 𝒪 (s ) ¯e0 + − 2-sR a0cω + 𝒪(s ) ¯eb, [ ] p¨αa(t) = [˙aa + 𝒪 (s )]¯eα0 + aaab + 𝒪 (s) ¯eαb,

as well as Equation (221

) for $Δ ≡ t − u$ . Our final result is

[ 1 1 ] eαa = δba + -s2ab(t)aa(t) + --s2Rba0c(t)ωc + 𝒪 (s3) ¯eαb [ 2( ) 2 ] 1 b 1 2 1 2 b 3 α + − s 1 − -sabω aa(t) + -s ˙aa(t) − -s Ra0b0(u)ω + 𝒪 (s ) ¯e0. (227 ) 2 2 2

3.4.4 Advanced point

It will prove convenient to introduce on the world line, along with the retarded and simultaneous points, an advanced point associated with the field point $x$ . The advanced point will be denoted $′′ x ≡ z(v)$ , with $v$ denoting the value of the proper-time parameter at $x′′$ ; to tensors at this point we assign indices $α ′′$ , $β ′′$ , etc. The advanced point is linked to $x$ by a past-directed null geodesic (refer back to Figure 8 ), and it can be located by solving $σ(x,x ′′) = 0$ together with the requirement that $σα′′(x,x′′)$ be a future-directed null vector. The affine-parameter distance between $x$ and $′′ x$ along the null geodesic is given by

and we shall call this the advanced distance between $x$ and the world line. Notice that $radv$ is a positive quantity.

We wish first to find an expression for $v$ in terms of the retarded coordinates of $x$ . For this purpose we define $Δ ′ ≡ v − u$ and re-introduce the function $σ (τ) ≡ σ(x,z(τ ))$ first considered in Section 3.4.2. We have that $σ (v ) = σ(u) = 0$ , and $Δ ′$ can ultimately be obtained by expressing $σ(v)$ as $σ(u + Δ ′)$ and expanding in powers of $Δ′$ . Recalling that $σ˙(τ ) = p(τ)$ , we have

1 1 1 σ(v) = σ(u) + p(u)Δ ′ +--˙p(u)Δ′2 + -¨p(u)Δ ′3 + ---p(3)(u)Δ′4 + 𝒪(Δ ′5). 2 6 24

Using the expressions for the derivatives of $p(τ)$ that were first obtained in Section 3.4.1, we write this as

[ ] 1- a 1-2 3 ′ 1- a ′2 1-- ′3 ′4 r = 2 1 + raaΩ + 3r S + 𝒪 (r ) Δ + 6 r[˙a0 + ˙aaΩ + 𝒪 (r)]Δ − 24 [a˙0 + 𝒪 (r)]Δ + 𝒪 (Δ ).

Solving for $Δ′$ as an expansion in powers of $r$ , we obtain

{ } a 2 a2 1 2 2 2 a 1 2 a b 3 v = u + 2r 1− raa(u)Ω + r [aa(u)Ω ] − 3r ˙a0(u) − 3r a˙a (u )Ω − 3r Ra0b0(u)Ω Ω + 𝒪 (r ) , (229 )

in which all frame components are evaluated at the retarded point $z(u)$ .

Our next task is to derive an expression for the advanced distance $radv$ . For this purpose we observe that $′ radv = − p(v) = − p (u + Δ )$ , which we can expand in powers of $′ Δ ≡ v − u$ . This gives