3.3 Retarded coordinates
3.3.1 Geometrical elements
We introduce the same geometrical elements as in Section 3.2: We have a timelike curve 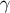 described by
relations
described by
relations 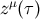 , its normalized tangent vector
, its normalized tangent vector 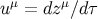 , and its acceleration vector
, and its acceleration vector 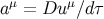 .
We also have an orthonormal triad
.
We also have an orthonormal triad 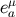 that is transported on the world line according to
that is transported on the world line according to
where  are the frame components of the acceleration vector and
are the frame components of the acceleration vector and 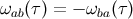 is a
prescribed rotation tensor. Here the triad is not Fermi–Walker transported: For added generality we allow
the spatial vectors to rotate as they are transported on the world line. While
is a
prescribed rotation tensor. Here the triad is not Fermi–Walker transported: For added generality we allow
the spatial vectors to rotate as they are transported on the world line. While 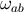 will be set to zero in
most sections of this paper, the freedom to perform such a rotation can be useful and will be exploited in
Section 5.4. It is easy to check that Equation (138) is compatible with the requirement that the tetrad
will be set to zero in
most sections of this paper, the freedom to perform such a rotation can be useful and will be exploited in
Section 5.4. It is easy to check that Equation (138) is compatible with the requirement that the tetrad
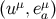 be orthonormal everywhere on
be orthonormal everywhere on 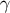 . Finally, we have a dual tetrad
. Finally, we have a dual tetrad 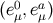 , with
, with
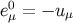 and
and 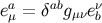 . The tetrad and its dual give rise to the completeness relations
which are the same as in Equation (115).
. The tetrad and its dual give rise to the completeness relations
which are the same as in Equation (115).
The Fermi normal coordinates of Section 3.2 were constructed on the basis of a spacelike geodesic
connecting a field point 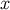 to the world line. The retarded coordinates are based instead on a null geodesic
going from the world line to the field point. We thus let
to the world line. The retarded coordinates are based instead on a null geodesic
going from the world line to the field point. We thus let 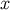 be within the normal convex neighbourhood of
be within the normal convex neighbourhood of
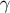 ,
, 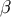 be the unique future-directed null geodesic that goes from the world line to
be the unique future-directed null geodesic that goes from the world line to 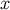 , and
, and 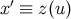 be the point at which
be the point at which 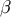 intersects the world line, with
intersects the world line, with 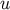 denoting the value of the proper-time
parameter at this point.
denoting the value of the proper-time
parameter at this point.
From the tetrad at 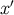 we obtain another tetrad
we obtain another tetrad 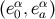 at
at 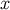 by parallel transport on
by parallel transport on
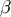 . By raising the frame index and lowering the vectorial index we also obtain a dual tetrad
at
. By raising the frame index and lowering the vectorial index we also obtain a dual tetrad
at 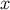 :
: 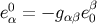 and
and 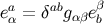 . The metric at
. The metric at 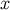 can be then be expressed as
can be then be expressed as
and the parallel propagator from 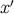 to
to 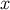 is given by
is given by
3.3.2 Definition of the retarded coordinates
The quasi-Cartesian version of the retarded coordinates are defined by
the last statement indicates that 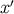 and
and 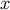 are linked by a null geodesic. From the fact that
are linked by a null geodesic. From the fact that 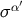 is a
null vector we obtain
and
is a
null vector we obtain
and 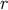 is a positive quantity by virtue of the fact that
is a positive quantity by virtue of the fact that 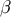 is a future-directed null geodesic – this makes
is a future-directed null geodesic – this makes
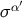 past-directed. In flat spacetime,
past-directed. In flat spacetime, 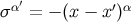 , and in a Lorentz frame that is momentarily
comoving with the world line,
, and in a Lorentz frame that is momentarily
comoving with the world line, 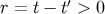 ; with the speed of light set equal to unity,
; with the speed of light set equal to unity, 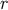 is also the
spatial distance between
is also the
spatial distance between 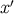 and
and 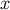 as measured in this frame. In curved spacetime, the quantity
as measured in this frame. In curved spacetime, the quantity
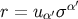 can still be called the retarded distance between the point
can still be called the retarded distance between the point 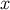 and the world line. Another
consequence of Equation (142) is that
where
and the world line. Another
consequence of Equation (142) is that
where 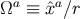 is a spatial vector that satisfies
is a spatial vector that satisfies 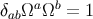 .
.
A straightforward calculation reveals that under a displacement of the point 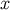 , the retarded
coordinates change according to
, the retarded
coordinates change according to
where 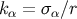 is a future-directed null vector at
is a future-directed null vector at 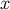 that is tangent to the geodesic
that is tangent to the geodesic 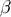 . To obtain
these results we must keep in mind that a displacement of
. To obtain
these results we must keep in mind that a displacement of 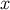 typically induces a simultaneous
displacement of
typically induces a simultaneous
displacement of 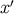 because the new points
because the new points 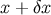 and
and 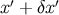 must also be linked by a null
geodesic. We therefore have
must also be linked by a null
geodesic. We therefore have 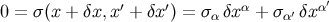 , and the first relation of
Equation (145) follows from the fact that a displacement along the world line is described by
, and the first relation of
Equation (145) follows from the fact that a displacement along the world line is described by
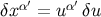 .
.
3.3.3 The scalar field 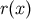 and the vector field
and the vector field 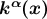
If we keep 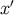 linked to
linked to 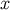 by the relation
by the relation 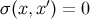 , then the quantity
, then the quantity
can be viewed as an ordinary scalar field defined in a neighbourhood of 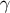 . We can compute the gradient
of
. We can compute the gradient
of 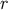 by finding how
by finding how 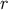 changes under a displacement of
changes under a displacement of 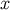 (which again induces a displacement of
(which again induces a displacement of
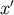 ). The result is
). The result is
Similarly, we can view
as an ordinary vector field, which is tangent to the congruence of null geodesics that emanate from 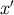 . It
is easy to check that this vector satisfies the identities
from which we also obtain
. It
is easy to check that this vector satisfies the identities
from which we also obtain 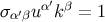 . From this last result and Equation (147) we deduce the
important relation
In addition, combining the general statement
. From this last result and Equation (147) we deduce the
important relation
In addition, combining the general statement 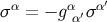 (cf. Equation (79)) with Equation (144)
gives
the vector at
(cf. Equation (79)) with Equation (144)
gives
the vector at 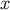 is therefore obtained by parallel transport of
is therefore obtained by parallel transport of 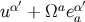 on
on 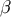 . From this and
Equation (141) we get the alternative expression
which confirms that
. From this and
Equation (141) we get the alternative expression
which confirms that 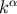 is a future-directed null vector field (recall that
is a future-directed null vector field (recall that 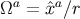 is a unit
vector).
is a unit
vector).
The covariant derivative of 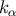 can be computed by finding how the vector changes under a
displacement of
can be computed by finding how the vector changes under a
displacement of 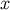 . (It is in fact easier to first calculate how
. (It is in fact easier to first calculate how 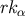 changes, and then substitute our
previous expression for
changes, and then substitute our
previous expression for 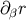 .) The result is
.) The result is
From this we infer that 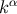 satisfies the geodesic equation in affine-parameter form,
satisfies the geodesic equation in affine-parameter form, 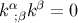 , and
Equation (150) informs us that the affine parameter is in fact
, and
Equation (150) informs us that the affine parameter is in fact 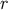 . A displacement along a member of the
congruence is therefore given by
. A displacement along a member of the
congruence is therefore given by 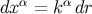 . Specializing to retarded coordinates, and using
Equations (145) and (149), we find that this statement becomes
. Specializing to retarded coordinates, and using
Equations (145) and (149), we find that this statement becomes  and
and 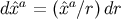 , which
integrate to
, which
integrate to 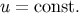 and
and 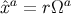 , respectively, with
, respectively, with 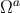 still denoting a constant unit
vector. We have found that the congruence of null geodesics emanating from
still denoting a constant unit
vector. We have found that the congruence of null geodesics emanating from 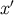 is described by
in the retarded coordinates. Here, the two angles
is described by
in the retarded coordinates. Here, the two angles 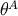 (
(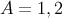 ) serve to parameterize the unit vector
) serve to parameterize the unit vector
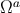 , which is independent of
, which is independent of 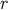 .
.
Equation (153) also implies that the expansion of the congruence is given by
Using the expansion for 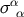 given by Equation (91), we find that this becomes
given by Equation (91), we find that this becomes 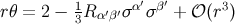 ,
or
after using Equation (144). Here,
,
or
after using Equation (144). Here, 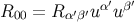 ,
, 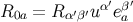 , and
, and 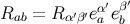 are the
frame components of the Ricci tensor evaluated at
are the
frame components of the Ricci tensor evaluated at 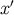 . This result confirms that the congruence is singular
at
. This result confirms that the congruence is singular
at 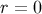 , because
, because 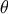 diverges as
diverges as 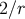 in this limit; the caustic coincides with the point
in this limit; the caustic coincides with the point
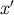 .
.
Finally, we infer from Equation (153) that 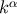 is hypersurface orthogonal. This, together with the
property that
is hypersurface orthogonal. This, together with the
property that 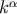 satisfies the geodesic equation in affine-parameter form, implies that there exists a scalar
field
satisfies the geodesic equation in affine-parameter form, implies that there exists a scalar
field 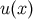 such that
such that
This scalar field was already identified in Equation (145): It is numerically equal to the proper-time
parameter of the world line at 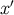 . We conclude that the geodesics to which
. We conclude that the geodesics to which 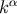 is tangent are the
generators of the null cone
is tangent are the
generators of the null cone 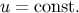 As Equation (154) indicates, a specific generator is selected by
choosing a direction
As Equation (154) indicates, a specific generator is selected by
choosing a direction 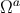 (which can be parameterized by two angles
(which can be parameterized by two angles 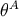 ), and
), and 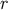 is an affine parameter
on each generator. The geometrical meaning of the retarded coordinates is now completely clear; it is
illustrated in Figure 7.
is an affine parameter
on each generator. The geometrical meaning of the retarded coordinates is now completely clear; it is
illustrated in Figure 7.
3.3.4 Frame components of tensor fields on the world line
The metric at 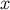 in the retarded coordinates will be expressed in terms of frame components of vectors
and tensors evaluated on the world line
in the retarded coordinates will be expressed in terms of frame components of vectors
and tensors evaluated on the world line 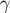 . For example, if
. For example, if 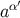 is the acceleration vector at
is the acceleration vector at 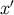 , then as
we have seen,
, then as
we have seen,
are the frame components of the acceleration at proper time  .
.
Similarly,
are the frame components of the Riemann tensor evaluated on 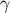 . From these we form the useful
combinations
in which the quantities
. From these we form the useful
combinations
in which the quantities 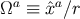 depend on the angles
depend on the angles 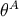 only – they are independent of
only – they are independent of 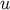 and
and
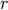 .
.
We have previously introduced the frame components of the Ricci tensor in Equation (156). The
identity
follows easily from Equations (160, 161, 162) and the definition of the Ricci tensor.
In Section 3.2 we saw that the frame components of a given tensor were also the components of this
tensor (evaluated on the world line) in the Fermi normal coordinates. We should not expect this property to
be true also in the case of the retarded coordinates: the frame components of a tensor are not to be
identified with the components of this tensor in the retarded coordinates. The reason is that the retarded
coordinates are in fact singular on the world line. As we shall see, they give rise to a metric that
possesses a directional ambiguity at 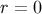 . (This can easily be seen in Minkowski spacetime by
performing the coordinate transformation
. (This can easily be seen in Minkowski spacetime by
performing the coordinate transformation 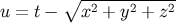 .) Components of tensors are
therefore not defined on the world line, although they are perfectly well defined for
.) Components of tensors are
therefore not defined on the world line, although they are perfectly well defined for 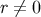 .
Frame components, on the other hand, are well defined both off and on the world line, and
working with them will eliminate any difficulty associated with the singular nature of the retarded
coordinates.
.
Frame components, on the other hand, are well defined both off and on the world line, and
working with them will eliminate any difficulty associated with the singular nature of the retarded
coordinates.
3.3.5 Coordinate displacements near 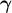
The changes in the quasi-Cartesian retarded coordinates under a displacement of 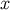 are given by
Equation (145). In these we substitute the standard expansions for
are given by
Equation (145). In these we substitute the standard expansions for 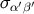 and
and 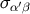 , as given by
Equations (88) and (89), as well as Equations (144) and (151). After a straightforward (but
fairly lengthy) calculation, we obtain the following expressions for the coordinate displacements:
, as given by
Equations (88) and (89), as well as Equations (144) and (151). After a straightforward (but
fairly lengthy) calculation, we obtain the following expressions for the coordinate displacements:
Notice that the result for 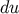 is exact, but that
is exact, but that 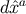 is expressed as an expansion in powers of
is expressed as an expansion in powers of
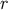 .
.
These results can also be expressed in the form of gradients of the retarded coordinates:
Notice that Equation (166) follows immediately from Equations (152) and (157). From Equation (167)
and the identity 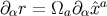 we also infer
where we have used the facts that
we also infer
where we have used the facts that 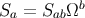 and
and 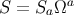 ; these last results were derived in
Equations (161) and (162). It may be checked that Equation (168) agrees with Equation (147).
; these last results were derived in
Equations (161) and (162). It may be checked that Equation (168) agrees with Equation (147).
3.3.6 Metric near 
It is straightforward (but fairly tedious) to invert the relations of Equations (164) and (165) and solve for
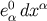 and
and 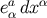 . The results are
. The results are
These relations, when specialized to the retarded coordinates, give us the components of the dual tetrad
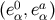 at
at 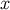 . The metric is then computed by using the completeness relations of Equation (140). We
find
. The metric is then computed by using the completeness relations of Equation (140). We
find
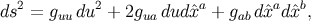
with
We see (as was pointed out in Section 3.3.4) that the metric possesses a directional ambiguity on the world
line: The metric at  still depends on the vector
still depends on the vector 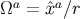 that specifies the direction to the point
that specifies the direction to the point
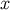 . The retarded coordinates are therefore singular on the world line, and tensor components cannot be
defined on
. The retarded coordinates are therefore singular on the world line, and tensor components cannot be
defined on 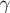 .
.
By setting 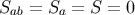 in Equations (171, 172, 173) we obtain the metric of flat spacetime in
the retarded coordinates. This we express as
in Equations (171, 172, 173) we obtain the metric of flat spacetime in
the retarded coordinates. This we express as
In spite of the directional ambiguity, the metric of flat spacetime has a unit determinant everywhere, and it
is easily inverted:
The inverse metric also is ambiguous on the world line.
To invert the curved-spacetime metric of Equations (171, 172, 173) we express it as
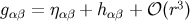 and treat
and treat 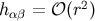 as a perturbation. The inverse metric is then
as a perturbation. The inverse metric is then
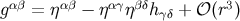 , or
, or
The results for 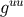 and
and 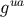 are exact, and they follow from the general relations
are exact, and they follow from the general relations 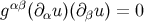 and
and 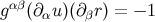 that are derived from Equations (150) and (157).
that are derived from Equations (150) and (157).
The metric determinant is computed from 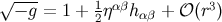 , which gives
, which gives
where we have substituted the identity of Equation (163). Comparison with Equation (156) then gives us
the interesting relation 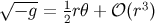 , where
, where 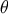 is the expansion of the generators of the null
cones
is the expansion of the generators of the null
cones 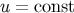 .
.
3.3.7 Transformation to angular coordinates
Because the vector 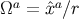 satisfies
satisfies 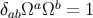 , it can be parameterized by two angles
, it can be parameterized by two angles 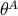 . A
canonical choice for the parameterization is
. A
canonical choice for the parameterization is 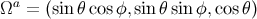 . It is then convenient to
perform a coordinate transformation from
. It is then convenient to
perform a coordinate transformation from 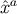 to
to 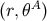 , using the relations
, using the relations  . (Recall
from Section 3.3.3 that the angles
. (Recall
from Section 3.3.3 that the angles 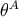 are constant on the generators of the null cones
are constant on the generators of the null cones 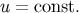 ,
and that
,
and that 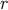 is an affine parameter on these generators. The relations
is an affine parameter on these generators. The relations 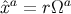 therefore
describe the behaviour of the generators.) The differential form of the coordinate transformation is
therefore
describe the behaviour of the generators.) The differential form of the coordinate transformation is
where the transformation matrix
satisfies the identity 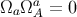 .
.
We introduce the quantities
which act as a (nonphysical) metric in the subspace spanned by the angular coordinates. In the canonical
parameterization, 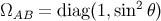 . We use the inverse of
. We use the inverse of 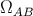 , denoted
, denoted 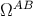 , to raise upper-case
latin indices. We then define the new object
which satisfies the identities
The second result follows from the fact that both sides are simultaneously symmetric in
, to raise upper-case
latin indices. We then define the new object
which satisfies the identities
The second result follows from the fact that both sides are simultaneously symmetric in 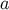 and
and 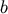 ,
orthogonal to
,
orthogonal to 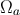 and
and 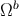 , and have the same trace.
, and have the same trace.
From the preceding results we establish that the transformation from  to
to 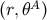 is accomplished
by
is accomplished
by
while the transformation from 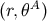 to
to  is accomplished by
With these transformation rules it is easy to show that in the angular coordinates, the metric takes the form
of
is accomplished by
With these transformation rules it is easy to show that in the angular coordinates, the metric takes the form
of
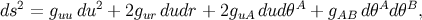
with
The results 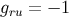 ,
, 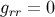 , and
, and 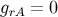 are exact, and they follow from the fact that in the
retarded coordinates,
are exact, and they follow from the fact that in the
retarded coordinates, 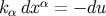 and
and 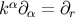 .
.
The nonvanishing components of the inverse metric are
The results 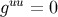 ,
, 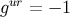 , and
, and 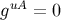 are exact, and they follow from the same reasoning as
before.
are exact, and they follow from the same reasoning as
before.
Finally, we note that in the angular coordinates, the metric determinant is given by
where 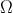 is the determinant of
is the determinant of 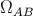 ; in the canonical parameterization,
; in the canonical parameterization, 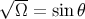 .
.
3.3.8 Specialization to 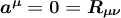
In this section we specialize our previous results to a situation where 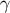 is a geodesic on which the Ricci
tensor vanishes. We therefore set
is a geodesic on which the Ricci
tensor vanishes. We therefore set 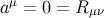 everywhere on
everywhere on 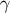 , and for simplicity we also set
, and for simplicity we also set 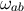 to
zero.
to
zero.
We have seen in Section 3.2.6 that when the Ricci tensor vanishes on 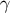 , all frame components of the
Riemann tensor can be expressed in terms of the symmetric-tracefree tensors
, all frame components of the
Riemann tensor can be expressed in terms of the symmetric-tracefree tensors 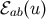 and
and 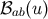 . The
relations are
. The
relations are 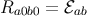 ,
, 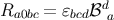 , and
, and 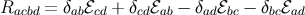 . These can be
substituted into Equations (160, 161, 162) to give
. These can be
substituted into Equations (160, 161, 162) to give
In these expressions the dependence on retarded time  is contained in
is contained in 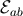 and
and 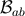 , while the angular
dependence is encoded in the unit vector
, while the angular
dependence is encoded in the unit vector 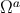 .
.
It is convenient to introduce the irreducible quantities
These are all orthogonal to 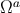 :
: 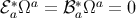 and
and 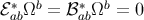 . In terms of these
Equations (196, 197, 198) become
. In terms of these
Equations (196, 197, 198) become
When Equations (204, 205, 206) are substituted into the metric tensor of Equations (171, 172, 173)
– in which 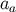 and
and 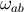 are both set equal to zero – we obtain the compact expressions
are both set equal to zero – we obtain the compact expressions
The metric becomes
after transforming to angular coordinates using the rules of Equation (185). Here we have introduced the
projections
It may be noted that the inverse relations are 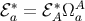 ,
, 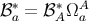 ,
,  , and
, and
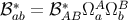 , where
, where 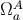 was introduced in Equation (183).
was introduced in Equation (183).
![]() described by
relations
described by
relations ![]() , its normalized tangent vector
, its normalized tangent vector ![]() , and its acceleration vector
, and its acceleration vector ![]() .
We also have an orthonormal triad
.
We also have an orthonormal triad ![]() that is transported on the world line according to
that is transported on the world line according to
![]() to the world line. The retarded coordinates are based instead on a null geodesic
going from the world line to the field point. We thus let
to the world line. The retarded coordinates are based instead on a null geodesic
going from the world line to the field point. We thus let ![]() be within the normal convex neighbourhood of
be within the normal convex neighbourhood of
![]() ,
, ![]() be the unique future-directed null geodesic that goes from the world line to
be the unique future-directed null geodesic that goes from the world line to ![]() , and
, and ![]() be the point at which
be the point at which ![]() intersects the world line, with
intersects the world line, with ![]() denoting the value of the proper-time
parameter at this point.
denoting the value of the proper-time
parameter at this point.
![]() we obtain another tetrad
we obtain another tetrad ![]() at
at ![]() by parallel transport on
by parallel transport on
![]() . By raising the frame index and lowering the vectorial index we also obtain a dual tetrad
at
. By raising the frame index and lowering the vectorial index we also obtain a dual tetrad
at ![]() :
: ![]() and
and ![]() . The metric at
. The metric at ![]() can be then be expressed as
can be then be expressed as
![]() , the retarded
coordinates change according to
, the retarded
coordinates change according to ![]() linked to
linked to ![]() by the relation
by the relation ![]() , then the quantity
, then the quantity ![]() can be computed by finding how the vector changes under a
displacement of
can be computed by finding how the vector changes under a
displacement of ![]() . (It is in fact easier to first calculate how
. (It is in fact easier to first calculate how ![]() changes, and then substitute our
previous expression for
changes, and then substitute our
previous expression for ![]() .) The result is
.) The result is ![]() ) also implies that the expansion of the congruence is given by
) also implies that the expansion of the congruence is given by ![]() ) that
) that ![]() is hypersurface orthogonal. This, together with the
property that
is hypersurface orthogonal. This, together with the
property that ![]() satisfies the geodesic equation in affine-parameter form, implies that there exists a scalar
field
satisfies the geodesic equation in affine-parameter form, implies that there exists a scalar
field ![]() such that
such that ![]() in the retarded coordinates will be expressed in terms of frame components of vectors
and tensors evaluated on the world line
in the retarded coordinates will be expressed in terms of frame components of vectors
and tensors evaluated on the world line ![]() . For example, if
. For example, if ![]() is the acceleration vector at
is the acceleration vector at ![]() , then as
we have seen,
, then as
we have seen, ![]() ). The
identity
). The
identity ![]() . (This can easily be seen in Minkowski spacetime by
performing the coordinate transformation
. (This can easily be seen in Minkowski spacetime by
performing the coordinate transformation ![]() .) Components of tensors are
therefore not defined on the world line, although they are perfectly well defined for
.) Components of tensors are
therefore not defined on the world line, although they are perfectly well defined for ![]() .
Frame components, on the other hand, are well defined both off and on the world line, and
working with them will eliminate any difficulty associated with the singular nature of the retarded
coordinates.
.
Frame components, on the other hand, are well defined both off and on the world line, and
working with them will eliminate any difficulty associated with the singular nature of the retarded
coordinates.
![]() are given by
Equation (145
are given by
Equation (145![]() ). In these we substitute the standard expansions for
). In these we substitute the standard expansions for ![]() and
and ![]() , as given by
Equations (88
, as given by
Equations (88![]() ) and (89
) and (89![]() ), as well as Equations (144
), as well as Equations (144![]() ) and (151
) and (151![]() ). After a straightforward (but
fairly lengthy) calculation, we obtain the following expressions for the coordinate displacements:
). After a straightforward (but
fairly lengthy) calculation, we obtain the following expressions for the coordinate displacements:
![]() ) and (165
) and (165![]() ) and solve for
) and solve for
![]() and
and ![]() . The results are
. The results are ![]() in Equations (171
in Equations (171![]() , 172
, 172![]() , 173
, 173![]() ) we obtain the metric of flat spacetime in
the retarded coordinates. This we express as
) we obtain the metric of flat spacetime in
the retarded coordinates. This we express as ![]() , 172
, 172![]() , 173
, 173![]() ) we express it as
) we express it as
![]() and treat
and treat ![]() as a perturbation. The inverse metric is then
as a perturbation. The inverse metric is then
![]() , or
, or ![]() , which gives
, which gives ![]() satisfies
satisfies ![]() , it can be parameterized by two angles
, it can be parameterized by two angles ![]() . A
canonical choice for the parameterization is
. A
canonical choice for the parameterization is ![]() . It is then convenient to
perform a coordinate transformation from
. It is then convenient to
perform a coordinate transformation from ![]() to
to ![]() , using the relations
, using the relations ![]() . (Recall
from Section 3.3.3 that the angles
. (Recall
from Section 3.3.3 that the angles ![]() are constant on the generators of the null cones
are constant on the generators of the null cones ![]() ,
and that
,
and that ![]() is an affine parameter on these generators. The relations
is an affine parameter on these generators. The relations ![]() therefore
describe the behaviour of the generators.) The differential form of the coordinate transformation is
therefore
describe the behaviour of the generators.) The differential form of the coordinate transformation is
![]() to
to ![]() is accomplished
by
is accomplished
by ![]() is a geodesic on which the Ricci
tensor vanishes. We therefore set
is a geodesic on which the Ricci
tensor vanishes. We therefore set ![]() everywhere on
everywhere on ![]() , and for simplicity we also set
, and for simplicity we also set ![]() to
zero.
to
zero.
![]() , all frame components of the
Riemann tensor can be expressed in terms of the symmetric-tracefree tensors
, all frame components of the
Riemann tensor can be expressed in terms of the symmetric-tracefree tensors ![]() and
and ![]() . The
relations are
. The
relations are ![]() ,
, ![]() , and
, and ![]() . These can be
substituted into Equations (160
. These can be
substituted into Equations (160![]() , 161
, 161![]() , 162
, 162![]() ) to give
) to give ![]() , 205
, 205![]() , 206
, 206![]() ) are substituted into the metric tensor of Equations (171
) are substituted into the metric tensor of Equations (171![]() , 172
, 172![]() , 173
, 173![]() )
– in which
)
– in which ![]() and
and ![]() are both set equal to zero – we obtain the compact expressions
are both set equal to zero – we obtain the compact expressions