Electromagnetic Green’s functions

4.4 Electromagnetic Green’s functions

4.4.1 Equations of electromagnetism

The electromagnetic field tensor $F αβ = ∇ αA β − ∇ βA α$ is expressed in terms of a vector potential $Aα$ . In the Lorenz gauge $α ∇ αA = 0$ , the vector potential satisfies the wave equation

where $□ = gαβ∇ ∇ α β$ is the wave operator, $R α β$ the Ricci tensor, and $jα$ a prescribed current density. The wave equation enforces the condition $α ∇ αj = 0$ , which expresses charge conservation.

The solution to the wave equation is written as

in terms of a Green’s function $α ′ G β′(x, x)$ that satisfies

where $gα ′(x,x ′) β$ is a parallel propagator and $δ (x, x′) 4$ an invariant Dirac distribution. The parallel propagator is inserted on the right-hand side of Equation (316

) to keep the index structure of the equation consistent from side to side; because $α ′ ′ g β′(x, x)δ4(x,x )$ is distributionally equal to $[gαβ′]δ4(x,x′) = δαβ′′δ4(x,x′)$ , it could have been replaced by either $δα′β′$ or $δαβ$ . It is easy to check that by virtue of Equation (316

), the vector potential of Equation (315

) satisfies the wave equation of Equation (314

We will assume that the retarded Green’s function $α ′ G +β′(x, x)$ , which is nonzero if $x$ is in the causal future of $x ′$ , and the advanced Green’s function $G−αβ′(x,x ′)$ , which is nonzero if $x$ is in the causal past of $x ′$ , exist as distributions and can be defined globally in the entire spacetime.

4.4.2 Hadamard construction of the Green’s functions

Assuming throughout this section that $x$ is in the normal convex neighbourhood of $x ′$ , we make the ansatz

where $θ±(− σ)$ , $δ±(σ)$ are the light-cone distributions introduced in Section 4.2.2, and where $U αβ′(x,x ′)$ , $Vαβ′(x,x ′)$ are smooth bitensors.

To conveniently manipulate the Green’s functions we shift $σ$ by a small positive quantity $ε$ . The Green’s functions are then recovered by the taking the limit of

Gε± αβ′(x,x′) ≡ U αβ′(x,x′)δ± (σ + ε) + V αβ′(x,x′)θ±(− σ − ε)

as $+ ε → 0$ . When we substitute this into the left-hand side of Equation (316 ) and then take the limit, we obtain

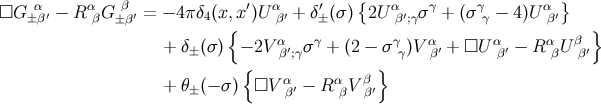
□G α′ − R αG β′ = − 4πδ4(x,x ′)U α′ + δ′(σ){2U α′ σγ + (σγ − 4)U α′} ±β β ±β { β ± β ;γ γ β } + δ± (σ) − 2Vαβ′;γσγ + (2 − σγγ)V αβ′ + □U αβ′ − R αβU β′ { } β + θ (− σ ) □V α′ − R αV β′ ± β β β

after a routine computation similar to the one presented at the beginning of Section 4.3.2. Comparison with Equation (316

) returns

the equations

and

that determine $α ′ U β′(x,x )$ ;
the equation

that determines $ˇV αβ′(x,x′)$ , the restriction of $V αβ′(x,x′)$ on the light cone $σ(x, x′) = 0$ ; and
the wave equation

that determines $V α′(x,x′) β$ inside the light cone.

Equation (319 ) can be integrated along the unique geodesic $β$ that links $′ x$ to $x$ . The initial conditions are provided by Equation (318 ), and if we set $α ′ α ′ ′ U β′(x, x) = g β′(x,x )U(x,x )$ , we find that these equations reduce to Equations (272 ) and (271 ), respectively. According to Equation (273 ), then, we have

which reduces to

near coincidence, with $λ$ denoting the affine-parameter distance between $′ x$ and $x$ . Differentiation of this relation gives

( ) α 1 γ′ α α′ 1 α δ′ 2 U β′;γ = 2g γ g α′R β′γ′δ′ − 3g β′R γ′δ′ σ + 𝒪 (λ ), (324 ) ( ) α 1- α α′ 1- α δ′ 2 U β′;γ′ = 2 g α′R β′γ′δ′ + 3 gβ′R γ′δ′ σ + 𝒪 (λ ), (325 )

and eventually,

Similarly, Equation (320 ) can be integrated along each null geodesic that generates the null cone $′ σ(x,x ) = 0$ . The initial values are obtained by taking the coincidence limit of this equation, using Equations (318 ), (326 ), and the additional relation $γ [σ γ] = 4$ . We arrive at

With the characteristic data obtained by integrating Equation (320

), the wave equation of Equation (321

) admits a unique solution.

To summarize, the retarded and advanced electromagnetic Green’s functions are given by Equation (317 ) with $U α′(x,x′) β$ given by Equation (322 ) and $V α′(x, x′) β$ determined by Equation (321 ) and the characteristic data constructed with Equations (320 ) and (327 ). It should be emphasized that the construction provided in this section is restricted to $𝒩 (x′)$ , the normal convex neighbourhood of the reference point $x ′$ .

4.4.3 Reciprocity and Kirchhoff representation

Like their scalar counterparts, the (globally defined) electromagnetic Green’s functions satisfy a reciprocity relation, the statement of which is

The derivation of Equation (328

) is virtually identical to what was presented in Section 4.3.3, and we shall not present the details. It suffices to mention that it is based on the identities

( ) G+αβ′(x, x′) □G −αγ′′(x, x′′) − RαγG −γγ′′(x,x ′′) = − 4πG+αβ′(x,x′)gαγ′′(x,x′′)δ4(x,x′&#x203

and

( γ ) G−αγ′′(x,x ′′) □G α+β′(x, x′) − R αγG +β′(x,x′) = − 4πG −αγ′′(x,x′′)gαβ′(x, x′)δ4(x,x ′).

A direct consequence of the reciprocity relation is

the statement that the bitensor $V ′(x,x′) αβ$ is symmetric in its indices and arguments.

The Kirchhoff representation for the electromagnetic vector potential is formulated as follows. Suppose that $A α(x)$ satisfies the homogeneous version of Equation (314 ) and that initial values $′ A α(x′)$ , $n β′∇ β′Aα′(x′)$ are specified on a spacelike hypersurface $Σ$ . Then the value of the potential at a point $x$ in the future of $Σ$ is given by

where $dΣ ′ = − n ′dV γ γ$ is a surface element on $Σ$ ; $n ′ γ$ is the future-directed unit normal and $dV$ is the invariant volume element on the hypersurface. The derivation of Equation (330

) is virtually identical to what was presented in Section 4.3.4.

4.4.4 Singular and radiative Green’s functions

We shall now construct singular and radiative Green’s functions for the electromagnetic field. The treatment here parallels closely what was presented in Section 4.3.5, and the reader is referred to that section for a more complete discussion.

We begin by introducing the bitensor $H αβ′(x,x ′)$ with properties

Em.H1: $α ′ H β′(x, x)$ satisfies the homogeneous wave equation,

Em.H2: $H αβ′(x, x′)$ is symmetric in its indices and arguments,

Em.H3: $α ′ H β′(x, x)$ agrees with the retarded Green’s function if $x$ is in the chronological future of $x′$ ,

Em.H4: $H α ′(x, x′) β$ agrees with the advanced Green’s function if $x$ is in the chronological past of $x′$ ,

It is easy to prove that Property Em.H4 follows from Property Em.H2, Property Em.H3, and the reciprocity relation (328 ) satisfied by the retarded and advanced Green’s functions. That such a bitensor exists can be argued along the same lines as those presented in Section 4.3.5.

Equipped with the bitensor $α ′ H β′(x, x)$ we define the singular Green’s function to be

This comes with the properties

Em.S1: $α ′ G Sβ′(x, x)$ satisfies the inhomogeneous wave equation,

Em.S2: $G Sαβ′(x, x′)$ is symmetric in its indices and arguments,

Em.S3: $G Sαβ′(x, x′)$ vanishes if $x$ is in the chronological past or future of $x ′$ ,

These can be established as consequences of Properties Em.H1, Em.H2, Em.H3, and Em.H4, and the properties of the retarded and advanced Green’s functions.

The radiative Green’s function is then defined by

and it comes with the properties

Em.R1: $α ′ G Rβ′(x,x )$ satisfies the homogeneous wave equation,

Em.R2: $G Rαβ′(x,x′)$ agrees with the retarded Green’s function if $x$ is in the chronological future of $x ′$

Em.R3: $G α′(x,x′) Rβ$ vanishes if $x$ is in the chronological past of $x′$ ,

Those follow immediately from Properties Em.S1, Em.S2, and Em.S3 and the properties of the retarded Green’s function.

When $x$ is restricted to the normal convex neighbourhood of $′ x$ , we have the explicit relations

H αβ′(x, x′) = V αβ′(x,x′), (343 ) 1 1 G αSβ′(x, x′) = -U αβ′(x,x′)δ(σ ) − -V αβ′(x,x′)θ(σ), (344 ) 2 2 [ ] α ′ 1- α ′ α ′ 1- GR β′(x, x) = 2U β′(x,x )[δ+(σ) − δ− (σ)] + V β′(x,x ) θ+(− σ) + 2θ(σ ) . (345 )

From these we see clearly that the singular Green’s function does not distinguish between past and future (Property Em.S2), and that its support excludes $I±(x′)$ (Property Em.S3). We see also that the radiative Green’s function coincides with $G α ′(x,x ′) + β$ in $I+(x′)$ (Property Em.R2), and that its support does not include $I− (x ′)$ (Property Em.R3).