2 Randall–Sundrum Brane-Worlds
RS brane-worlds do not rely on compactification to localize gravity at the brane, but on the
curvature of the bulk (sometimes called “warped compactification”). What prevents gravity from
‘leaking’ into the extra dimension at low energies is a negative bulk cosmological constant,
where 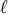 is the curvature radius of
is the curvature radius of 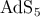 and
and 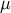 is the corresponding energy scale. The curvature
radius determines the magnitude of the Riemann tensor:
The bulk cosmological constant acts to “squeeze” the gravitational field closer to the brane. We can see this
clearly in Gaussian normal coordinates
is the corresponding energy scale. The curvature
radius determines the magnitude of the Riemann tensor:
The bulk cosmological constant acts to “squeeze” the gravitational field closer to the brane. We can see this
clearly in Gaussian normal coordinates 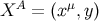 based on the brane at
based on the brane at 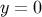 , for which the
, for which the 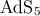 metric takes the form
with
metric takes the form
with  being the Minkowski metric. The exponential warp factor reflects the confining role of the bulk
cosmological constant. The
being the Minkowski metric. The exponential warp factor reflects the confining role of the bulk
cosmological constant. The 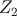 -symmetry about the brane at
-symmetry about the brane at 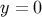 is incorporated via the
is incorporated via the 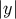 term.
In the bulk, this metric is a solution of the 5D Einstein equations,
i.e.,
term.
In the bulk, this metric is a solution of the 5D Einstein equations,
i.e.,  in Equation (2). The brane is a flat Minkowski spacetime,
in Equation (2). The brane is a flat Minkowski spacetime, 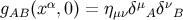 , with
self-gravity in the form of brane tension. One can also use Poincare coordinates, which bring the metric into
manifestly conformally flat form,
where
, with
self-gravity in the form of brane tension. One can also use Poincare coordinates, which bring the metric into
manifestly conformally flat form,
where 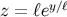 .
.
The two RS models are distinguished as follows:
-
RS 2-brane:
- There are two branes in this model [266], at
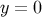 and
and 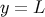 , with
, with 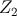 -symmetry
identifications
The branes have equal and opposite tensions
-symmetry
identifications
The branes have equal and opposite tensions 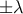 , where
The positive-tension brane has fundamental scale
, where
The positive-tension brane has fundamental scale 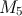 and is “hidden”. Standard model fields are
confined on the negative tension (or “visible”) brane. Because of the exponential warping factor, the
effective scale on the visible brane at
and is “hidden”. Standard model fields are
confined on the negative tension (or “visible”) brane. Because of the exponential warping factor, the
effective scale on the visible brane at 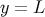 is
is  , where
So the RS 2-brane model gives a new approach to the hierarchy problem. Because of the finite
separation between the branes, the KK spectrum is discrete. Furthermore, at low energies gravity on
the branes becomes Brans–Dicke-like, with the sign of the Brans–Dicke parameter equal to the sign of
the brane tension [106
, where
So the RS 2-brane model gives a new approach to the hierarchy problem. Because of the finite
separation between the branes, the KK spectrum is discrete. Furthermore, at low energies gravity on
the branes becomes Brans–Dicke-like, with the sign of the Brans–Dicke parameter equal to the sign of
the brane tension [106 ]. In order to recover 4D general relativity at low energies, a mechanism is
required to stabilize the inter-brane distance, which corresponds to a scalar field degree of freedom
known as the radion [120, 202
]. In order to recover 4D general relativity at low energies, a mechanism is
required to stabilize the inter-brane distance, which corresponds to a scalar field degree of freedom
known as the radion [120, 202 , 248
, 248 , 305
, 305 ].
].
-
RS 1-brane:
- In this model [265
 ], there is only one, positive tension, brane. It may be thought of as arising
from sending the negative tension brane off to infinity,
], there is only one, positive tension, brane. It may be thought of as arising
from sending the negative tension brane off to infinity, 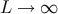 . Then the energy scales are related
via
The infinite extra dimension makes a finite contribution to the 5D volume because of the warp factor:
Thus the effective size of the extra dimension probed by the 5D graviton is
. Then the energy scales are related
via
The infinite extra dimension makes a finite contribution to the 5D volume because of the warp factor:
Thus the effective size of the extra dimension probed by the 5D graviton is 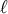 .
.
I will concentrate mainly on RS 1-brane from now on, referring to RS 2-brane occasionally. The
RS 1-brane models are in some sense the most simple and geometrically appealing form of
a brane-world model, while at the same time providing a framework for the AdS/CFT
correspondence [87 , 125
, 125 , 136
, 136 , 210
, 210 , 254
, 254 , 259
, 259 , 282
, 282 , 289
, 289 , 293
, 293 ]. The RS 2-brane introduce the added
complication of radion stabilization, as well as possible complications arising from negative tension.
However, they remain important and will occasionally be discussed.
]. The RS 2-brane introduce the added
complication of radion stabilization, as well as possible complications arising from negative tension.
However, they remain important and will occasionally be discussed.
In RS 1-brane, the negative  is offset by the positive brane tension
is offset by the positive brane tension  . The fine-tuning in
Equation (25) ensures that there is a zero effective cosmological constant on the brane, so that
the brane has the induced geometry of Minkowski spacetime. To see how gravity is localized
at low energies, we consider the 5D graviton perturbations of the metric [81, 106
. The fine-tuning in
Equation (25) ensures that there is a zero effective cosmological constant on the brane, so that
the brane has the induced geometry of Minkowski spacetime. To see how gravity is localized
at low energies, we consider the 5D graviton perturbations of the metric [81, 106 , 117, 265],
, 117, 265],
(see Figure 3). This is the RS gauge, which is different from the gauge used in Equation (15), but which
also has no remaining gauge freedom. The 5 polarizations of the 5D graviton are contained in the 5
independent components of 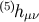 in the RS gauge.
in the RS gauge.
We split the amplitude  of
of 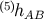 into 3D Fourier modes, and the linearized 5D Einstein equations
lead to the wave equation (
into 3D Fourier modes, and the linearized 5D Einstein equations
lead to the wave equation ( )
)
Separability means that we can write
and the wave equation reduces to
The zero mode solution is
and the  solutions are
The boundary condition for the perturbations arises from the junction conditions, Equation (62), discussed
below, and leads to
solutions are
The boundary condition for the perturbations arises from the junction conditions, Equation (62), discussed
below, and leads to 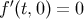 , since the transverse traceless part of the perturbed energy-momentum
tensor on the brane vanishes. This implies
The zero mode is normalizable, since
Its contribution to the gravitational potential
, since the transverse traceless part of the perturbed energy-momentum
tensor on the brane vanishes. This implies
The zero mode is normalizable, since
Its contribution to the gravitational potential  gives the 4D result,
gives the 4D result, 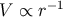 . The
contribution of the massive KK modes sums to a correction of the 4D potential. For
. The
contribution of the massive KK modes sums to a correction of the 4D potential. For 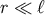 , one obtains
which simply reflects the fact that the potential becomes truly 5D on small scales. For
, one obtains
which simply reflects the fact that the potential becomes truly 5D on small scales. For 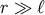 ,
which gives the small correction to 4D gravity at low energies from extra-dimensional effects. These effects
serve to slightly strengthen the gravitational field, as expected.
,
which gives the small correction to 4D gravity at low energies from extra-dimensional effects. These effects
serve to slightly strengthen the gravitational field, as expected.
Table-top tests of Newton’s laws currently find no deviations down to 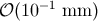 , so that
, so that
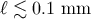 in Equation (41). Then by Equations (25) and (27), this leads to lower limits on the brane
tension and the fundamental scale of the RS 1-brane model:
in Equation (41). Then by Equations (25) and (27), this leads to lower limits on the brane
tension and the fundamental scale of the RS 1-brane model:
These limits do not apply to the 2-brane case.
For the 1-brane model, the boundary condition, Equation (38), admits a continuous spectrum 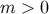 of KK modes. In the 2-brane model,
of KK modes. In the 2-brane model, 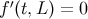 must hold in addition to Equation (38). This leads to
conditions on
must hold in addition to Equation (38). This leads to
conditions on 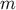 , so that the KK spectrum is discrete:
, so that the KK spectrum is discrete:
The limit Equation (42) indicates that there are no observable collider, i.e., 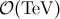 , signatures for
the RS 1-brane model. The 2-brane model by contrast, for suitable choice of
, signatures for
the RS 1-brane model. The 2-brane model by contrast, for suitable choice of 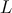 and
and 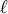 so
that
so
that 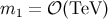 , does predict collider signatures that are distinct from those of the ADD
models [132, 137].
, does predict collider signatures that are distinct from those of the ADD
models [132, 137].
![]() , 125
, 125![]() , 136
, 136![]() , 210
, 210![]() , 254
, 254![]() , 259
, 259![]() , 282
, 282![]() , 289
, 289![]() , 293
, 293![]() ]. The RS 2-brane introduce the added
complication of radion stabilization, as well as possible complications arising from negative tension.
However, they remain important and will occasionally be discussed.
]. The RS 2-brane introduce the added
complication of radion stabilization, as well as possible complications arising from negative tension.
However, they remain important and will occasionally be discussed.
![]() is offset by the positive brane tension
is offset by the positive brane tension ![]() . The fine-tuning in
Equation (25
. The fine-tuning in
Equation (25![]() ) ensures that there is a zero effective cosmological constant on the brane, so that
the brane has the induced geometry of Minkowski spacetime. To see how gravity is localized
at low energies, we consider the 5D graviton perturbations of the metric [81, 106
) ensures that there is a zero effective cosmological constant on the brane, so that
the brane has the induced geometry of Minkowski spacetime. To see how gravity is localized
at low energies, we consider the 5D graviton perturbations of the metric [81, 106![]() , 117, 265],
, 117, 265],
![]() of
of ![]() into 3D Fourier modes, and the linearized 5D Einstein equations
lead to the wave equation (
into 3D Fourier modes, and the linearized 5D Einstein equations
lead to the wave equation (![]() )
) ![]() , so that
, so that
![]() in Equation (41
in Equation (41![]() ). Then by Equations (25
). Then by Equations (25![]() ) and (27
) and (27![]() ), this leads to lower limits on the brane
tension and the fundamental scale of the RS 1-brane model:
), this leads to lower limits on the brane
tension and the fundamental scale of the RS 1-brane model: ![]() ), admits a continuous spectrum
), admits a continuous spectrum ![]() of KK modes. In the 2-brane model,
of KK modes. In the 2-brane model, ![]() must hold in addition to Equation (38
must hold in addition to Equation (38![]() ). This leads to
conditions on
). This leads to
conditions on ![]() , so that the KK spectrum is discrete:
, so that the KK spectrum is discrete: