5.1 Brane-world inflation
In 1-brane RS-type brane-worlds, where the bulk has only a vacuum energy, inflation on the brane must
be driven by a 4D scalar field trapped on the brane. In more general brane-worlds, where the bulk contains
a 5D scalar field, it is possible that the 5D field induces inflation on the brane via its effective
projection [13 , 33
, 33 , 100
, 100 , 103
, 103 , 138
, 138 , 139
, 139 , 140
, 140 , 141
, 141 , 158
, 158 , 165
, 165 , 180
, 180 , 195
, 195 , 229
, 229 , 238
, 238 , 276
, 276 , 304
, 304 , 318
, 318 ].
].
More exotic possibilities arise from the interaction between two branes, including possible collision,
which is mediated by a 5D scalar field and which can induce either inflation [90 , 157
, 157 ] or a hot big-bang
radiation era, as in the “ekpyrotic” or cyclic scenario [154
] or a hot big-bang
radiation era, as in the “ekpyrotic” or cyclic scenario [154 , 163
, 163 , 193
, 193 , 231
, 231 , 251
, 251 , 301
, 301 , 307
, 307 ], or in colliding
bubble scenarios [29
], or in colliding
bubble scenarios [29 , 107
, 107 , 108
, 108 ]. (See also [21
]. (See also [21 , 69
, 69 , 214
, 214 ] for colliding branes in an M theory approach.) Here
we discuss the simplest case of a 4D scalar field
] for colliding branes in an M theory approach.) Here
we discuss the simplest case of a 4D scalar field  with potential
with potential 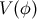 (see [207] for a
review).
(see [207] for a
review).
High-energy brane-world modifications to the dynamics of inflation on the brane have been
investigated [23, 24, 25, 63, 74, 135, 156, 184, 204, 221, 222 , 233, 234, 240, 270, 302]. Essentially, the
high-energy corrections provide increased Hubble damping, since
, 233, 234, 240, 270, 302]. Essentially, the
high-energy corrections provide increased Hubble damping, since 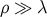 implies that
implies that  is larger for a
given energy than in 4D general relativity. This makes slow-roll inflation possible even for potentials that
would be too steep in standard cosmology [70
is larger for a
given energy than in 4D general relativity. This makes slow-roll inflation possible even for potentials that
would be too steep in standard cosmology [70 , 145
, 145 , 206
, 206 , 222
, 222 , 226
, 226 , 258
, 258 , 277
, 277 ].
].
The field satisfies the Klein–Gordon equation
In 4D general relativity, the condition for inflation, 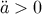 , is
, is 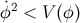 , i.e.,
, i.e., 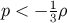 , where
, where
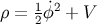 and
and  . The modified Friedmann equation leads to a stronger condition for
inflation: Using Equation (188), with
. The modified Friedmann equation leads to a stronger condition for
inflation: Using Equation (188), with 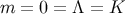 , and Equation (198), we find that
where the square brackets enclose the brane correction to the general relativity result. As
, and Equation (198), we find that
where the square brackets enclose the brane correction to the general relativity result. As 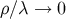 , the
4D result
, the
4D result 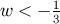 is recovered, but for
is recovered, but for  ,
,  must be more negative for inflation. In the very
high-energy limit
must be more negative for inflation. In the very
high-energy limit 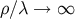 , we have
, we have 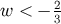 . When the only matter in the universe is a
self-interacting scalar field, the condition for inflation becomes
which reduces to
. When the only matter in the universe is a
self-interacting scalar field, the condition for inflation becomes
which reduces to 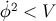 when
when 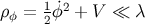 .
.
In the slow-roll approximation, we get
The brane-world correction term  in Equation (201) serves to enhance the Hubble rate for a given
potential energy, relative to general relativity. Thus there is enhanced Hubble ‘friction’ in Equation (202),
and brane-world effects will reinforce slow-roll at the same potential energy. We can see this by
defining slow-roll parameters that reduce to the standard parameters in the low-energy limit:
Self-consistency of the slow-roll approximation then requires
in Equation (201) serves to enhance the Hubble rate for a given
potential energy, relative to general relativity. Thus there is enhanced Hubble ‘friction’ in Equation (202),
and brane-world effects will reinforce slow-roll at the same potential energy. We can see this by
defining slow-roll parameters that reduce to the standard parameters in the low-energy limit:
Self-consistency of the slow-roll approximation then requires 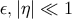 . At low energies,
. At low energies, 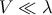 , the
slow-roll parameters reduce to the standard form. However at high energies,
, the
slow-roll parameters reduce to the standard form. However at high energies, 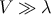 , the extra
contribution to the Hubble expansion helps damp the rolling of the scalar field, and the new factors in
square brackets become
, the extra
contribution to the Hubble expansion helps damp the rolling of the scalar field, and the new factors in
square brackets become 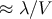 :
where
:
where  are the standard general relativity slow-roll parameters. In particular, this means that steep
potentials which do not give inflation in general relativity, can inflate the brane-world at high energy and
then naturally stop inflating when
are the standard general relativity slow-roll parameters. In particular, this means that steep
potentials which do not give inflation in general relativity, can inflate the brane-world at high energy and
then naturally stop inflating when 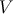 drops below
drops below 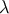 . These models can be constrained because
they typically end inflation in a kinetic-dominated regime and thus generate a blue spectrum
of gravitational waves, which can disturb nucleosynthesis [70
. These models can be constrained because
they typically end inflation in a kinetic-dominated regime and thus generate a blue spectrum
of gravitational waves, which can disturb nucleosynthesis [70 , 206
, 206 , 226
, 226 , 258
, 258 , 277
, 277 ]. They also
allow for the novel possibility that the inflaton could act as dark matter or quintessence at low
energies [4, 43, 70
]. They also
allow for the novel possibility that the inflaton could act as dark matter or quintessence at low
energies [4, 43, 70 , 206
, 206 , 208, 226
, 208, 226 , 239, 258
, 239, 258 , 277
, 277 , 285].
, 285].
The number of e-folds during inflation, 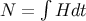 , is, in the slow-roll approximation,
, is, in the slow-roll approximation,
Brane-world effects at high energies increase the Hubble rate by a factor 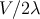 , yielding more inflation
between any two values of
, yielding more inflation
between any two values of 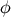 for a given potential. Thus we can obtain a given number of e-folds for a
smaller initial inflaton value
for a given potential. Thus we can obtain a given number of e-folds for a
smaller initial inflaton value  . For
. For  , Equation (206) becomes
, Equation (206) becomes
The key test of any modified gravity theory during inflation will be the spectrum of perturbations
produced due to quantum fluctuations of the fields about their homogeneous background values. We will
discuss brane-world cosmological perturbations in the next Section 6. In general, perturbations
on the brane are coupled to bulk metric perturbations, and the problem is very complicated.
However, on large scales on the brane, the density perturbations decouple from the bulk metric
perturbations [102 , 122
, 122 , 191
, 191 , 218
, 218 ]. For 1-brane RS-type models, there is no scalar zero-mode
of the bulk graviton, and in the extreme slow-roll (de Sitter) limit, the massive scalar modes
are heavy and stay in their vacuum state during inflation [102
]. For 1-brane RS-type models, there is no scalar zero-mode
of the bulk graviton, and in the extreme slow-roll (de Sitter) limit, the massive scalar modes
are heavy and stay in their vacuum state during inflation [102 ]. Thus it seems a reasonable
approximation in slow-roll to neglect the KK effects carried by
]. Thus it seems a reasonable
approximation in slow-roll to neglect the KK effects carried by  when computing the density
perturbations.
when computing the density
perturbations.
To quantify the amplitude of scalar (density) perturbations we evaluate the usual gauge-invariant
quantity
which reduces to the curvature perturbation 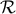 on uniform density hypersurfaces (
on uniform density hypersurfaces ( ). This is
conserved on large scales for purely adiabatic perturbations as a consequence of energy conservation
(independently of the field equations) [317
). This is
conserved on large scales for purely adiabatic perturbations as a consequence of energy conservation
(independently of the field equations) [317 ]. The curvature perturbation on uniform density
hypersurfaces is given in terms of the scalar field fluctuations on spatially flat hypersurfaces
]. The curvature perturbation on uniform density
hypersurfaces is given in terms of the scalar field fluctuations on spatially flat hypersurfaces 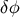 by
The field fluctuations at Hubble crossing (
by
The field fluctuations at Hubble crossing ( ) in the slow-roll limit are given by
) in the slow-roll limit are given by  ,
a result for a massless field in de Sitter space that is also independent of the gravity theory [317]. For a
single scalar field the perturbations are adiabatic and hence the curvature perturbation
,
a result for a massless field in de Sitter space that is also independent of the gravity theory [317]. For a
single scalar field the perturbations are adiabatic and hence the curvature perturbation  can be related
to the density perturbations when modes re-enter the Hubble scale during the matter dominated era
which is given by
can be related
to the density perturbations when modes re-enter the Hubble scale during the matter dominated era
which is given by  . Using the slow-roll equations and Equation (209), this gives
Thus the amplitude of scalar perturbations is increased relative to the standard result at a fixed value of
. Using the slow-roll equations and Equation (209), this gives
Thus the amplitude of scalar perturbations is increased relative to the standard result at a fixed value of
 for a given potential.
for a given potential.
The scale-dependence of the perturbations is described by the spectral tilt
where the slow-roll parameters are given in Equations (203) and (204). Because these slow-roll parameters
are both suppressed by an extra factor  at high energies, we see that the spectral index is driven
towards the Harrison–Zel’dovich spectrum,
at high energies, we see that the spectral index is driven
towards the Harrison–Zel’dovich spectrum,  , as
, as  ; however, as explained below, this
does not necessarily mean that the brane-world case is closer to scale-invariance than the general relativity
case.
; however, as explained below, this
does not necessarily mean that the brane-world case is closer to scale-invariance than the general relativity
case.
As an example, consider the simplest chaotic inflation model 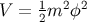 . Equation (206) gives the
integrated expansion from
. Equation (206) gives the
integrated expansion from 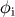 to
to  as
as
The new high-energy term on the right leads to more inflation for a given initial inflaton value
 .
.
The standard chaotic inflation scenario requires an inflaton mass 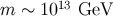 to match the
observed level of anisotropies in the cosmic microwave background (see below). This corresponds to
an energy scale
to match the
observed level of anisotropies in the cosmic microwave background (see below). This corresponds to
an energy scale 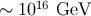 when the relevant scales left the Hubble scale during inflation,
and also to an inflaton field value of order
when the relevant scales left the Hubble scale during inflation,
and also to an inflaton field value of order 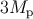 . Chaotic inflation has been criticised for
requiring super-Planckian field values, since these can lead to nonlinear quantum corrections in the
potential.
. Chaotic inflation has been criticised for
requiring super-Planckian field values, since these can lead to nonlinear quantum corrections in the
potential.
If the brane tension  is much below
is much below 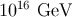 , corresponding to
, corresponding to 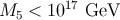 ,
then the terms quadratic in the energy density dominate the modified Friedmann equation. In
particular the condition for the end of inflation given in Equation (200) becomes
,
then the terms quadratic in the energy density dominate the modified Friedmann equation. In
particular the condition for the end of inflation given in Equation (200) becomes  . In the
slow-roll approximation (using Equations (201) and (202))
. In the
slow-roll approximation (using Equations (201) and (202)) 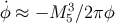 , and this yields
, and this yields
In order to estimate the value of  when scales corresponding to large-angle anisotropies on the
microwave background sky left the Hubble scale during inflation, we take
when scales corresponding to large-angle anisotropies on the
microwave background sky left the Hubble scale during inflation, we take  in Equation (212)
and
in Equation (212)
and  . The second term on the right of Equation (212) dominates, and we obtain
Imposing the COBE normalization on the curvature perturbations given by Equation (210) requires
Substituting in the value of
. The second term on the right of Equation (212) dominates, and we obtain
Imposing the COBE normalization on the curvature perturbations given by Equation (210) requires
Substituting in the value of  given by Equation (214) shows that in the limit of strong brane
corrections, observations require
Thus for
given by Equation (214) shows that in the limit of strong brane
corrections, observations require
Thus for 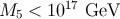 , chaotic inflation can occur for field values below the 4D Planck scale,
, chaotic inflation can occur for field values below the 4D Planck scale,
 , although still above the 5D scale
, although still above the 5D scale  . The relation determined by COBE constraints for
arbitrary brane tension is shown in Figure 5, together with the high-energy approximation used above,
which provides an excellent fit at low brane tension relative to
. The relation determined by COBE constraints for
arbitrary brane tension is shown in Figure 5, together with the high-energy approximation used above,
which provides an excellent fit at low brane tension relative to  .
.
It must be emphasized that in comparing the high-energy brane-world case to the standard 4D case, we
implicitly require the same potential energy. However, precisely because of the high-energy effects,
large-scale perturbations will be generated at different values of 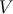 than in the standard case, specifically
at lower values of
than in the standard case, specifically
at lower values of 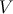 , closer to the reheating minimum. Thus there are two competing effects, and it turns
out that the shape of the potential determines which is the dominant effect [203
, closer to the reheating minimum. Thus there are two competing effects, and it turns
out that the shape of the potential determines which is the dominant effect [203 ]. For the quadratic
potential, the lower location on
]. For the quadratic
potential, the lower location on 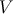 dominates, and the spectral tilt is slightly further from
scale invariance than in the standard case. The same holds for the quartic potential. Data from
WMAP and 2dF can be used to constrain inflationary models via their deviation from scale
invariance, and the high-energy brane-world versions of the quadratic and quartic potentials
are thus under more pressure from data than their standard counterparts [203
dominates, and the spectral tilt is slightly further from
scale invariance than in the standard case. The same holds for the quartic potential. Data from
WMAP and 2dF can be used to constrain inflationary models via their deviation from scale
invariance, and the high-energy brane-world versions of the quadratic and quartic potentials
are thus under more pressure from data than their standard counterparts [203 ], as shown in
Figure 6.
], as shown in
Figure 6.
Other perturbation modes have also been investigated:
- High-energy inflation on the brane also generates a zero-mode (4D graviton mode) of tensor
perturbations, and stretches it to super-Hubble scales, as will be discussed below. This
zero-mode has the same qualitative features as in general relativity, remaining frozen
at constant amplitude while beyond the Hubble horizon. Its amplitude is enhanced at
high energies, although the enhancement is much less than for scalar perturbations [192
 ]:
Equation (218) means that brane-world effects suppress the large-scale tensor contribution to CMB
anisotropies. The tensor spectral index at high energy has a smaller magnitude than in general
relativity,
but remarkably the same consistency relation as in general relativity holds [145]:
This consistency relation persists when
]:
Equation (218) means that brane-world effects suppress the large-scale tensor contribution to CMB
anisotropies. The tensor spectral index at high energy has a smaller magnitude than in general
relativity,
but remarkably the same consistency relation as in general relativity holds [145]:
This consistency relation persists when  symmetry is dropped [146] (and in a two-brane
model with stabilized radion [118]). It holds only to lowest order in slow-roll, as in general
relativity, but the reason for this [286] and the nature of the corrections [44] are not
settled.
symmetry is dropped [146] (and in a two-brane
model with stabilized radion [118]). It holds only to lowest order in slow-roll, as in general
relativity, but the reason for this [286] and the nature of the corrections [44] are not
settled.
The massive KK modes of tensor perturbations remain in the vacuum state during slow-roll
inflation [121 , 192
, 192 ]. The evolution of the super-Hubble zero mode is the same as in general relativity,
so that high-energy brane-world effects in the early universe serve only to rescale the amplitude.
However, when the zero mode re-enters the Hubble horizon, massive KK modes can be
excited.
]. The evolution of the super-Hubble zero mode is the same as in general relativity,
so that high-energy brane-world effects in the early universe serve only to rescale the amplitude.
However, when the zero mode re-enters the Hubble horizon, massive KK modes can be
excited.
- Vector perturbations in the bulk metric can support vector metric perturbations on the brane, even in
the absence of matter perturbations (see the next Section 6). However, there is no normalizable zero
mode, and the massive KK modes stay in the vacuum state during brane-world inflation [39].
Therefore, as in general relativity, we can neglect vector perturbations in inflationary
cosmology.
Brane-world effects on large-scale isocurvature perturbations in 2-field inflation have also been
considered [12]. Brane-world (p)reheating after inflation is discussed in [5, 67, 309, 310, 321].
![]() , 157
, 157![]() ] or a hot big-bang
radiation era, as in the “ekpyrotic” or cyclic scenario [154
] or a hot big-bang
radiation era, as in the “ekpyrotic” or cyclic scenario [154![]() , 163
, 163![]() , 193
, 193![]() , 231
, 231![]() , 251
, 251![]() , 301
, 301![]() , 307
, 307![]() ], or in colliding
bubble scenarios [29
], or in colliding
bubble scenarios [29![]() , 107
, 107![]() , 108
, 108![]() ]. (See also [21
]. (See also [21![]() , 69
, 69![]() , 214
, 214![]() ] for colliding branes in an M theory approach.) Here
we discuss the simplest case of a 4D scalar field
] for colliding branes in an M theory approach.) Here
we discuss the simplest case of a 4D scalar field ![]() with potential
with potential ![]() (see [207] for a
review).
(see [207] for a
review).
![]() , 233, 234, 240, 270, 302]. Essentially, the
high-energy corrections provide increased Hubble damping, since
, 233, 234, 240, 270, 302]. Essentially, the
high-energy corrections provide increased Hubble damping, since ![]() implies that
implies that ![]() is larger for a
given energy than in 4D general relativity. This makes slow-roll inflation possible even for potentials that
would be too steep in standard cosmology [70
is larger for a
given energy than in 4D general relativity. This makes slow-roll inflation possible even for potentials that
would be too steep in standard cosmology [70![]() , 145
, 145![]() , 206
, 206![]() , 222
, 222![]() , 226
, 226![]() , 258
, 258![]() , 277
, 277![]() ].
].
![]() , is, in the slow-roll approximation,
, is, in the slow-roll approximation,
![]() , 122
, 122![]() , 191
, 191![]() , 218
, 218![]() ]. For 1-brane RS-type models, there is no scalar zero-mode
of the bulk graviton, and in the extreme slow-roll (de Sitter) limit, the massive scalar modes
are heavy and stay in their vacuum state during inflation [102
]. For 1-brane RS-type models, there is no scalar zero-mode
of the bulk graviton, and in the extreme slow-roll (de Sitter) limit, the massive scalar modes
are heavy and stay in their vacuum state during inflation [102![]() ]. Thus it seems a reasonable
approximation in slow-roll to neglect the KK effects carried by
]. Thus it seems a reasonable
approximation in slow-roll to neglect the KK effects carried by ![]() when computing the density
perturbations.
when computing the density
perturbations.
![]() . Equation (206
. Equation (206![]() ) gives the
integrated expansion from
) gives the
integrated expansion from ![]() to
to ![]() as
as ![]() to match the
observed level of anisotropies in the cosmic microwave background (see below). This corresponds to
an energy scale
to match the
observed level of anisotropies in the cosmic microwave background (see below). This corresponds to
an energy scale ![]() when the relevant scales left the Hubble scale during inflation,
and also to an inflaton field value of order
when the relevant scales left the Hubble scale during inflation,
and also to an inflaton field value of order ![]() . Chaotic inflation has been criticised for
requiring super-Planckian field values, since these can lead to nonlinear quantum corrections in the
potential.
. Chaotic inflation has been criticised for
requiring super-Planckian field values, since these can lead to nonlinear quantum corrections in the
potential.
![]() is much below
is much below ![]() , corresponding to
, corresponding to ![]() ,
then the terms quadratic in the energy density dominate the modified Friedmann equation. In
particular the condition for the end of inflation given in Equation (200
,
then the terms quadratic in the energy density dominate the modified Friedmann equation. In
particular the condition for the end of inflation given in Equation (200![]() ) becomes
) becomes ![]() . In the
slow-roll approximation (using Equations (201
. In the
slow-roll approximation (using Equations (201![]() ) and (202
) and (202![]() ))
)) ![]() , and this yields
, and this yields
![]() than in the standard case, specifically
at lower values of
than in the standard case, specifically
at lower values of ![]() , closer to the reheating minimum. Thus there are two competing effects, and it turns
out that the shape of the potential determines which is the dominant effect [203
, closer to the reheating minimum. Thus there are two competing effects, and it turns
out that the shape of the potential determines which is the dominant effect [203![]() ]. For the quadratic
potential, the lower location on
]. For the quadratic
potential, the lower location on ![]() dominates, and the spectral tilt is slightly further from
scale invariance than in the standard case. The same holds for the quartic potential. Data from
WMAP and 2dF can be used to constrain inflationary models via their deviation from scale
invariance, and the high-energy brane-world versions of the quadratic and quartic potentials
are thus under more pressure from data than their standard counterparts [203
dominates, and the spectral tilt is slightly further from
scale invariance than in the standard case. The same holds for the quartic potential. Data from
WMAP and 2dF can be used to constrain inflationary models via their deviation from scale
invariance, and the high-energy brane-world versions of the quadratic and quartic potentials
are thus under more pressure from data than their standard counterparts [203![]() ], as shown in
Figure 6
], as shown in
Figure 6![]() .
.
![]() , 192
, 192![]() ]. The evolution of the super-Hubble zero mode is the same as in general relativity,
so that high-energy brane-world effects in the early universe serve only to rescale the amplitude.
However, when the zero mode re-enters the Hubble horizon, massive KK modes can be
excited.
]. The evolution of the super-Hubble zero mode is the same as in general relativity,
so that high-energy brane-world effects in the early universe serve only to rescale the amplitude.
However, when the zero mode re-enters the Hubble horizon, massive KK modes can be
excited.