- The simplest example arises from considering a charged bulk black hole, leading to the
Reissner–Nordström
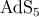 bulk metric [17
bulk metric [17 ]. This has the form of Equation (178), with
where
]. This has the form of Equation (178), with
where 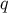 is the “electric” charge parameter of the bulk black hole. The metric is a solution of the 5D
Einstein–Maxwell equations, so that
is the “electric” charge parameter of the bulk black hole. The metric is a solution of the 5D
Einstein–Maxwell equations, so that 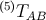 in Equation (44) is the energy-momentum tensor of a
radial static 5D “electric” field. In order for the field lines to terminate on the boundary brane, the
brane should carry a charge
in Equation (44) is the energy-momentum tensor of a
radial static 5D “electric” field. In order for the field lines to terminate on the boundary brane, the
brane should carry a charge  . Since the RN
. Since the RN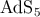 metric is 4-isotropic, it is still possible to
embed a FRW brane in it, which is moving in the coordinates of Equation (178). The effect of the
black hole charge on the brane arises via the junction conditions and leads to the modified Friedmann
equation [17],
The field lines that terminate on the brane imprint on the brane an effective negative
energy density
metric is 4-isotropic, it is still possible to
embed a FRW brane in it, which is moving in the coordinates of Equation (178). The effect of the
black hole charge on the brane arises via the junction conditions and leads to the modified Friedmann
equation [17],
The field lines that terminate on the brane imprint on the brane an effective negative
energy density  , which redshifts like stiff matter (
, which redshifts like stiff matter (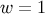 ). The negativity
of this term introduces the possibility that at high energies it can bring the expansion
rate to zero and cause a turn-around or bounce (but see [144] for problems with such
bounces).
). The negativity
of this term introduces the possibility that at high energies it can bring the expansion
rate to zero and cause a turn-around or bounce (but see [144] for problems with such
bounces).
Apart from negativity, the key difference between this “dark stiff matter” and the dark
radiation term  is that the latter arises from the bulk Weyl curvature via the
is that the latter arises from the bulk Weyl curvature via the  tensor, while the former arises from non-vacuum stresses in the bulk via the
tensor, while the former arises from non-vacuum stresses in the bulk via the  tensor
in Equation (63). The dark stiff matter does not arise from massive KK modes of the
graviton.
tensor
in Equation (63). The dark stiff matter does not arise from massive KK modes of the
graviton.
- Another example is provided by the Vaidya–
 metric, which can be written after transforming
to a new coordinate
metric, which can be written after transforming
to a new coordinate 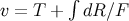 in Equation (178), so that
in Equation (178), so that 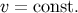 are null surfaces, and
This model has a moving FRW brane in a 4-isotropic bulk (which is not static), with either a
radiating bulk black hole (
are null surfaces, and
This model has a moving FRW brane in a 4-isotropic bulk (which is not static), with either a
radiating bulk black hole (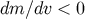 ), or a radiating brane (
), or a radiating brane ( ) [53, 197, 198, 199]. The
metric satisfies the 5D field equations (44) with a null-radiation energy-momentum tensor,
where
) [53, 197, 198, 199]. The
metric satisfies the 5D field equations (44) with a null-radiation energy-momentum tensor,
where 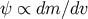 . It follows that
In this case, the same effect, i.e., a varying mass parameter
. It follows that
In this case, the same effect, i.e., a varying mass parameter 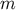 , contributes to both
, contributes to both 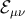 and
and  in the brane field equations. The modified Friedmann equation has the standard 1-brane
RS-type form, but with a dark radiation term that no longer behaves strictly like radiation:
in the brane field equations. The modified Friedmann equation has the standard 1-brane
RS-type form, but with a dark radiation term that no longer behaves strictly like radiation:
By Equations (68) and (228), we arrive at the matter conservation equations,
This shows how the brane loses (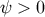 ) or gains (
) or gains (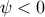 ) energy in exchange with the bulk black
hole. For an FRW brane, this equation reduces to
The evolution of
) energy in exchange with the bulk black
hole. For an FRW brane, this equation reduces to
The evolution of 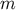 is governed by the 4D contracted Bianchi identity, using Equation (229):
For an FRW brane, this yields
where
is governed by the 4D contracted Bianchi identity, using Equation (229):
For an FRW brane, this yields
where  .
.
- A more complicated bulk metric arises when there is a self-interacting scalar field
 in the
bulk [16
in the
bulk [16 , 35
, 35 , 97
, 97 , 98
, 98 , 194
, 194 , 225
, 225 , 236
, 236 ]. In the simplest case, when there is no coupling between the bulk
field and brane matter, this gives
where
]. In the simplest case, when there is no coupling between the bulk
field and brane matter, this gives
where  satisfies the 5D Klein–Gordon equation,
The junction conditions on the field imply that
Then Equations (68) and (235) show that matter conservation continues to hold on the brane in this
simple case:
From Equation (235) one finds that
where
so that the modified Friedmann equation becomes
satisfies the 5D Klein–Gordon equation,
The junction conditions on the field imply that
Then Equations (68) and (235) show that matter conservation continues to hold on the brane in this
simple case:
From Equation (235) one finds that
where
so that the modified Friedmann equation becomes
When there is coupling between brane matter and the bulk scalar field, then the Friedmann and
conservation equations are more complicated [16 , 35
, 35 , 97
, 97 , 98
, 98 , 194
, 194 , 225
, 225 , 236
, 236 ].
].
![]() is that the latter arises from the bulk Weyl curvature via the
is that the latter arises from the bulk Weyl curvature via the ![]() tensor, while the former arises from non-vacuum stresses in the bulk via the
tensor, while the former arises from non-vacuum stresses in the bulk via the ![]() tensor
in Equation (63
tensor
in Equation (63![]() ). The dark stiff matter does not arise from massive KK modes of the
graviton.
). The dark stiff matter does not arise from massive KK modes of the
graviton.
![]() ) and (228
) and (228![]() ), we arrive at the matter conservation equations,
), we arrive at the matter conservation equations, ![]() , 35
, 35![]() , 97
, 97![]() , 98
, 98![]() , 194
, 194![]() , 225
, 225![]() , 236
, 236![]() ].
].