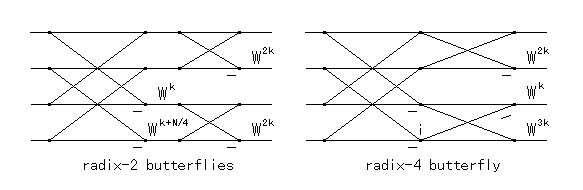
Split-Radix FFT は,いかなる基数の Cooley-Tukey FFT よりも 浮動小数点演算回数が少ないアルゴリズムとして知られています [参考文献]. Split-Radix FFT の説明の前に,なぜ大きい基数の FFT の演算量が 削減されるのかについて少し考えてみます.具体例として基数 4 の FFT の バタフライの構造について調べます.基数 4 の FFT は,基数 2 の FFT の 四つのバタフライ演算を,一つにまとめたものに相当します.このとき, 四つあった乗算は,三つに減ります.この変形は次のようになります.
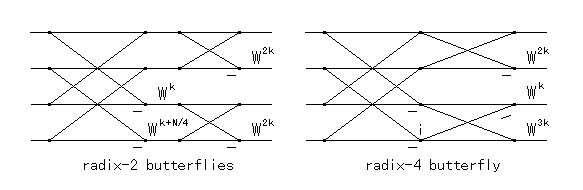 |
| 図1.2.4-1. 基数 2 と基数 4 のバタフライ |
|---|
この演算量の削減は,下半分のデータのバタフライ演算での,重なった 回転因子を一つにまとめることで行っていることがわかります.一方, 上半分のデータのバタフライ演算では演算の削減は行われておらず, 無意味な展開をしていることになります.この無意味な展開を削除したものが Split-Radix FFT アルゴリズムです.
Split-Radix FFT アルゴリズムは,偶数の添字の項に対しては,基数 2 の 分解を用い,奇数の添字の項に対しては,基数 4 の分解を用います. すなわち,DFT の基本式
N-1 jk -2πi / N
A = Σ a W , W = e
k j=0 j N N
を偶数項に関しては
N/2-1 jk
A = Σ (a + a ) W
2k j=0 j N/2+j N/2
と分解し,奇数項に対しては
N/4-1 j jk
A = Σ (a − a − i(a − a )) W W
4k+1 j=0 j N/2+j N/4+j 3N/4+j N N/4
N/4-1 3j jk
A = Σ (a − a + i(a − a )) W W
4k+3 j=0 j N/2+j N/4+j 3N/4+j N N/4
と分解します.この分解による Split-Radix FFT は L 字の形をした,異なる 深さのバタフライ演算で構成されます.このため,log(N) 段ある演算は, 単純に一段ずつ終了させることができず,構造が多少複雑になります.例えば, N = 8 の場合のフローグラフは次のようになります.
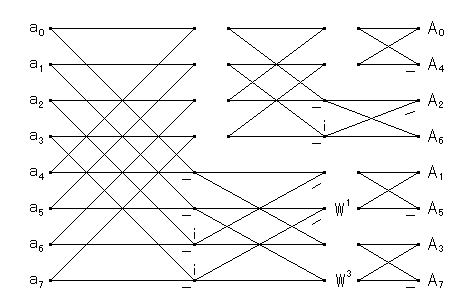 |
| 図1.2.4-2. Split-Radix FFT のデータフロー |
|---|
この L 字のバタフライ演算は,基数 2 の分解の部分では一段階しか進まず, 基数 4 の分解の部分で二段階進みます.また,最後の段で演算を完了させる ために,基数 2 の演算が別に必要になります.
次に,周波数間引きの Split-Radix FFT のルーチン例を示します.
| リスト1.2.4-1. Split-Radix FFT |
|---|
#include <math.h>
void fft(int n, double ar[], double ai[])
{
int m, mq, i, j, j1, j2, j3, k;
double theta, w1r, w1i, w3r, w3i;
double x0r, x0i, x1r, x1i, x3r, x3i;
/* ---- L shaped butterflies ---- */
theta = -8 * atan(1.0) / n;
for (m = n; m > 2; m >>= 1) {
mq = m >> 2;
for (i = 0; i < mq; i++) {
w1r = cos(theta * i);
w1i = sin(theta * i);
w3r = cos(theta * 3 * i);
w3i = sin(theta * 3 * i);
for (k = m; k <= n; k <<= 2) {
for (j = k - m + i; j < n; j += 2 * k) {
j1 = j + mq;
j2 = j1 + mq;
j3 = j2 + mq;
x1r = ar[j] - ar[j2];
x1i = ai[j] - ai[j2];
ar[j] += ar[j2];
ai[j] += ai[j2];
x3r = ar[j3] - ar[j1];
x3i = ai[j3] - ai[j1];
ar[j1] += ar[j3];
ai[j1] += ai[j3];
x0r = x1r - x3i;
x0i = x1i + x3r;
ar[j2] = w1r * x0r - w1i * x0i;
ai[j2] = w1r * x0i + w1i * x0r;
x0r = x1r + x3i;
x0i = x1i - x3r;
ar[j3] = w3r * x0r - w3i * x0i;
ai[j3] = w3r * x0i + w3i * x0r;
}
}
}
theta *= 2;
}
/* ---- radix 2 butterflies ---- */
for (k = 2; k <= n; k <<= 2) {
for (j = k - 2; j < n; j += 2 * k) {
x0r = ar[j] - ar[j + 1];
x0i = ai[j] - ai[j + 1];
ar[j] += ar[j + 1];
ai[j] += ai[j + 1];
ar[j + 1] = x0r;
ai[j + 1] = x0i;
}
}
/* ---- unscrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
x0r = ar[j];
x0i = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = x0r;
ai[i] = x0i;
}
}
}
|
このルーチンには,W=1,exp(πi/4) の場合に不要な乗算が含まれます. これらの不要な演算を取り除くためには,場合分けを行い,さらに二つの バタフライを追加します.基数が 2 のベキ乗の FFT の場合は 5 個の バタフライが必要ですが,Split-Radix FFT の場合は 3 個のバタフライで 済みます.さらに,高速化するためには内側のループでデータ参照を 連続にします.次に,これらの変更を施したルーチンの一例を示します.
| リスト1.2.4-2. 3バタフライの Split-Radix FFT |
|---|
#include <math.h>
void fft(int n, double ar[], double ai[])
{
int m, mq, irev, i, j, j1, j2, j3, k;
double theta, w1r, w1i, w3r, w3i;
double x0r, x0i, x1r, x1i, x3r, x3i;
/* ---- scrambler ---- */
i = 0;
for (j = 1; j < n - 1; j++) {
for (k = n >> 1; k > (i ^= k); k >>= 1);
if (j < i) {
x0r = ar[j];
x0i = ai[j];
ar[j] = ar[i];
ai[j] = ai[i];
ar[i] = x0r;
ai[i] = x0i;
}
}
/* ---- L shaped butterflies ---- */
theta = -2 * atan(1.0) / n;
for (m = 4; m <= n; m <<= 1) {
mq = m >> 2;
/* ---- W == 1 ---- */
for (k = mq; k >= 1; k >>= 2) {
for (j = mq - k; j < mq - (k >> 1); j++) {
j1 = j + mq;
j2 = j1 + mq;
j3 = j2 + mq;
x1r = ar[j] - ar[j1];
x1i = ai[j] - ai[j1];
ar[j] += ar[j1];
ai[j] += ai[j1];
x3r = ar[j3] - ar[j2];
x3i = ai[j3] - ai[j2];
ar[j2] += ar[j3];
ai[j2] += ai[j3];
ar[j1] = x1r - x3i;
ai[j1] = x1i + x3r;
ar[j3] = x1r + x3i;
ai[j3] = x1i - x3r;
}
}
if (m == n) continue;
/* ---- W == exp(-pi*i/4) ---- */
irev = n >> 1;
w1r = cos(theta * irev);
for (k = mq; k >= 1; k >>= 2) {
for (j = m + mq - k; j < m + mq - (k >> 1); j++) {
j1 = j + mq;
j2 = j1 + mq;
j3 = j2 + mq;
x1r = ar[j] - ar[j1];
x1i = ai[j] - ai[j1];
ar[j] += ar[j1];
ai[j] += ai[j1];
x3r = ar[j3] - ar[j2];
x3i = ai[j3] - ai[j2];
ar[j2] += ar[j3];
ai[j2] += ai[j3];
x0r = x1r - x3i;
x0i = x1i + x3r;
ar[j1] = w1r * (x0r + x0i);
ai[j1] = w1r * (x0i - x0r);
x0r = x1r + x3i;
x0i = x1i - x3r;
ar[j3] = w1r * (-x0r + x0i);
ai[j3] = w1r * (-x0i - x0r);
}
}
/* ---- W != 1, exp(-pi*i/4) ---- */
for (i = 2 * m; i < n; i += m) {
for (k = n >> 1; k > (irev ^= k); k >>= 1);
w1r = cos(theta * irev);
w1i = sin(theta * irev);
w3r = cos(theta * 3 * irev);
w3i = sin(theta * 3 * irev);
for (k = mq; k >= 1; k >>= 2) {
for (j = i + mq - k; j < i + mq - (k >> 1); j++) {
j1 = j + mq;
j2 = j1 + mq;
j3 = j2 + mq;
x1r = ar[j] - ar[j1];
x1i = ai[j] - ai[j1];
ar[j] += ar[j1];
ai[j] += ai[j1];
x3r = ar[j3] - ar[j2];
x3i = ai[j3] - ai[j2];
ar[j2] += ar[j3];
ai[j2] += ai[j3];
x0r = x1r - x3i;
x0i = x1i + x3r;
ar[j1] = w1r * x0r - w1i * x0i;
ai[j1] = w1r * x0i + w1i * x0r;
x0r = x1r + x3i;
x0i = x1i - x3r;
ar[j3] = w3r * x0r - w3i * x0i;
ai[j3] = w3r * x0i + w3i * x0r;
}
}
}
}
/* ---- radix 2 butterflies ---- */
mq = n >> 1;
for (k = mq; k >= 1; k >>= 2) {
for (j = mq - k; j < mq - (k >> 1); j++) {
j1 = mq + j;
x0r = ar[j] - ar[j1];
x0i = ai[j] - ai[j1];
ar[j] += ar[j1];
ai[j] += ai[j1];
ar[j1] = x0r;
ai[j1] = x0i;
}
}
}
|
次に,Split-Radix FFT の演算量について考えます.長さ N の複素 DFT の計算に必要な実数乗算回数 μ と実数加算回数 α は次のように なります.
4 38 2 log N
μ = --- N log N - ---- N + 6 + --- (-1)
3 9 9
8 16 2 log N
α = --- N log N - ---- N + 2 - --- (-1)
3 9 9
これは不要な演算を取り除く 3 バタフライルーチンを用いて,複素乗算を 4 回の実数乗算と 2 回の実数加算で計算したときの値です.これは,基数 4 の FFT に比べて乗算回数が約 8/9 に減り,加算回数が約 32/33 に減ります. さらに,複素乗算を 3 回の実数乗算と 3 回の実数加算で計算する方法を用いると,
μ = N log N - 3N + 4
α = 3N log N - 3N + 4
となります.これは,基数 2 の FFT に比べて加算回数はそのままで 乗算回数を約半分にした値です.Split-Radix FFT は,通常の Cooley-Tukey 型 FFT よりも複雑なループ構造となります.しかし,浮動小数点演算量は他の いかなる基数の FFT よりも少なくなります.また,長さが 16 以下の 場合には,Split-Radix FFT は理論的に最適な演算回数となることが わかっています.