The ADM representation

4.1 The ADM representation

In the ADM formulation of Einstein’s equations, the fields involved are detached from the under-laying space-time and brought into an abstract three dimensional manifold product a segment of the real line. To obtain the relation between these abstract fields and the metric tensor defining a solution of Einstein’s equations, we start by pretending we have such a solution, that is a space-time $(M, gab)$ . In this space-time we look at a Cauchy surface, $Σ 0$ , that is, an everywhere space-like hypersurface such that any in-extendible time-like piece-wise smooth curve pierces it once and only once, and a time flow, that is, a smooth time-like vector field, $ta$ . From the definition of the Cauchy surface, $ta$ is never tangent to it and every point of $M$ falls in an integral curve of $ta$ . Thus, in assuming the existence of $Σ0$ we are restricting attention to manifolds of the type $S × ℜ$ . To make this structure more apparent we define a function $t$ by setting to zero the parameter defining the integral curves of $a t$ at $Σ0$ , that is, the value of $t$ at $p ∈ M$ is defined as the value of the parameter the integral curve of $ta$ takes at $p$ if defined in such a way that at $Σ0$ is takes the value $0$ . We shall call the surfaces of constant $t$ by $Σt$ . Thus $ta∇at = 1$ , notice that nevertheless, in general, they are not space-like. When they are space-like, we shall call $t$ a time function. In this case we also say we have a space-like foliation of space-time $ab (M, g )$ . We shall assume that this is the case, but one must take into account that when we are solving for a space-time we do not know for how long this would continue to hold. Using this structure we can split tensor into “space” and “time” parts with respect to the surfaces $Σ t$ . If $na$ is the normal to them, that is, $na := − gab√--∇bt--- gcd∇ct∇dt$ then $hab := gab − nanb$ is the induced metric on each $Σt$ . We also define the lapse-shift pair, $(N, N a)$ , as the “time-like” and “space-like” parts of $ta$ with respect to $Σt$ , that is, $a a a t := N n + N$ .

Given the foliation, and the triad $(hab,N, N a)$ we can reconstruct the metric as $gab = hab − N −2(ta − N a)(tb − N b)$ . Given another foliation, $(Σ ,t′a) 0$ , but the same triad, we get another metric tensor, the relation between both is a diffeomorphism which leaves invariant $Σ0$ and is generated by the integral curves of $ta − t′a$ . Alternatively we can choose another pair $(N, N a)$ and so construct another metric tensor, the relation between both metric thus obtained is also a diffeomorphism. Since one is interested in geometries, that is in metric tensors up to diffeomorphisms, both metric obtained are equivalent, but one needs to pick up an specific one in order to write down, (and solve), Einstein’s equations.

Using the above splitting vacuum Einstein’s equations become two evolution equations:

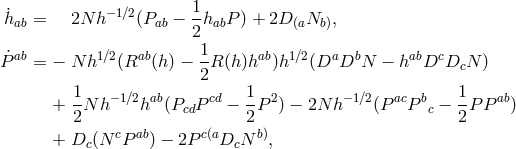
1 ˙hab = 2N h −1∕2(Pab − --habP) + 2D (aNb), 2 P˙ab = − N h1∕2(Rab(h) − 1-R(h)hab)h1∕2(DaDbN − habDcD N ) 2 c 1 −1∕2 ab cd 1 2 −1∕2 ac b 1 ab + --N h h (PcdP − -P ) − 2N h (P P c − -P P ) 2 c ab c(a 2b) 2 + Dc (N P ) − 2P DcN ,

where the dot means a Lie derivative with respect to $ta$ , $√ -- P ab := h(Kab − Khab )$ and $Kab$ is the extrinsic curvature of $Σt$ with respect to the four-geometry, that is, $ab ac b K := h ∇cn$ . $Da$ is the covariant derivative associated with $ab h$ on each $Σt$ , and $ab R$ its Ricci tensor.

And two constraint equations:

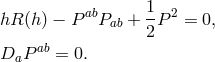
Note that there are two “dynamical” variables, $h ab$ , and $P ab$ , while the lapse-shift pair $(N, N a)$ , although necessary to determine the evolution, is undetermined by the equations. Note also that they do not enter into the constraint equations, for as said above a change on the lapse-shift pair leave the fields at initial surface unchanged.

It is important step back now and see that these equations can be thought as “living” in a structure completely detached from space-time. To see this, identify all points laying in the same integral curve of $a t$ , thus the equivalence class is a three dimensional manifold $S$ , homeomorphic to any $Σt$ . On it, for each $t$ we can induce space-contravariant tensors, such as $hab(t)$ , $Pab(t)$ , $Na (t)$ , and scalars, as $N (t)$ . As long as the surfaces are space-like, the induced metric is negative definite and we can invert it, thus we can perform all kinds of contractions and write the above equations as dynamical equations on the parameter $t$ on fields on the same manifold, $S$ . This is of course the setting in which one sets most of the schemes to solve the equations, and it is hard to keep control, even awareness, that the surfaces defining the foliation can become null or nearly so. Einstein’s equations “feel” that effect since they are causal, and this is abruptly fed back via the development of singularities on the solutions. They do not have any thing to do with real singularities of space-time, but rather with foliations becoming null.

The first application of this idea to Einstein’s equations appears to have been [18 ]. There a hyperbolic system consisting of wave equations for the time derivative of the variable $hhab$ is obtained when the shift is taken to vanish and the lapse is chosen so as to impose the time component of the harmonic gauge. The shift is set to zero, but, as stated in the paper, this is an unnecessary condition. Thus, it is clear that one gains in flexibility compared with the standard method above. This seems to correspond with the fact that in one of the equations forming the system, the time derivative of the evolution equation for the momentum, the momentum constraint has been suitably added, thus modifying the evolution flow outside the constraint sub-manifold. As stated in the paper, they could not use the other constraint, the Hamiltonian one, to modify that equation.

The condition for that system to be (symmetric) hyperbolic is that the term below should not have second derivatives of $ab P$ .

ab a b N˙- N-- (h Δ − D D )(N − 2 P),

where $ab h$ is the induced three metric on a hypersurface, $Da$ is the covariant derivative at that hypersurface compatible with $hab$ , $Δ := habDaDb$ , $N$ is the lapse function, and $P := habP ab$ , with $P ab$ the momentum field conjugated to $hab$ .

The simplest condition to guarantee this is:

2 ˙ N-- N = 2 P,

which in view of the definition of $ab P$ , which implies $h˙= hN P$ , has as a solution,

N = (h)1∕2, e

where $h e$ is the determinant of the metric $ab h$ with respect to a constant in time background metric $ab e$ . This is precisely the harmonic condition for the time component of $b Ψ$ in notation introduced in the paper’s introduction. That is, $Ψbnb ≡ 0$ , where $nb$ it the normal to the foliation. If the determinant of $eab$ is not taken to be constant in time, then one gets,

N˙-− N-P = ˙e, N 2 e

and so the system remains hyperbolic. Thus, we see that, up to the determinant of the metric, the lapse can be prescribed freely. This freedom is very important because it gives ductility to the approach, since this function can be specified according to the needs of applications. We shall call this a generalized harmonic time gauge.

Although in the introduction of [18 ] there is a remark dedicated to numerical relativists about the possible importance of having a stable system, the paper did not spark interest until recently, when applications required these results to proceed. In recent years, a number of papers have appeared which further elaborate on this system [2 , 3 , 4 ]. In particular, I would like to mention [3 ], where the authors look at the system in detail, writing it as a first order system, and introduce all variables which are needed for that. In these recent papers, the generalized harmonic time gauge has been included, as well as arbitrarily prescribed shift vectors. If one attempts attempts to write down the system as a first order one, that is, to give new names to the derivatives of the basic fields until bringing the system to the form of Equation 1 , the resulting system is rather big, it has fifty four variables, without counting the lapse-shift pair. We shall see that there are first order hyperbolic systems with half that number of variables.

Two similar results are of interest: In [9 ] a system is introduced with basically the same properties, but of lower order, that is, only first derivatives of the basic variables are taken as new independent variables in making the system first order. In this paper, it is realized that the same trick of modifying the evolution equations using the constraints can be done by modifying, instead of the second time derivative of the momentum, the extra equation which appears when making the ADM equations a first order system, that is the equation which fixes the time evolution of the space derivatives of the metric, or alternatively the time evolution of the Christoffel symbols. When this equation is suitably modified by adding a term proportional to the momentum constraint, and when the harmonic gauge in the generalized sense used above is imposed, a symmetric hyperbolic system results. In [10 ] the generalized harmonic time gauge is included, as well as arbitrarily prescribed shift vectors. For the latest on this approach see [11 ]. I shall comment more on this in Section 4.

In [30 ] a similar system is presented. In this case, the focus is on establishing some rigorous results in the Newtonian limit. So a conformal rescaling of the metric is employed using the lapse function as conformal factor. The immediate consequence of this transformation is to eliminate from the evolution equation for $Pab$ the term with second space derivatives of the lapse function, precisely the term giving rise to one of the terms in Equation 4.1. The end consequence is that the conformal metric is flatter to higher order. With this re-scaling, and using the same type of modification of the evolution equation for the space derivatives of the metric that the above two approaches use, a symmetric hyperbolic system is found, for arbitrary shift and lapse.⁸ This freedom of the lapse and shift was used to cancel several divergent terms of the energy integrals in the Newtonian limit by imposing an elliptic gauge condition on the shift, which also determined uniquely the lapse. This resulted in a mixed symmetric hyperbolic-elliptic system of equations. In [32 ] an attempt is made to explore what other possibilities there are of making symmetric hyperbolic systems for general relativity with arbitrarily prescribed lapse-shift pairs. A set of parametrized changes of field variables and of linear combinations of equations are made, and it is shown that there exists at least a one parameter family of symmetric hyperbolic systems. In these systems generalized harmonic time gauge is replaced by:

h N := (--)δ δ > 0. e

So, the dependence of the lapse on the determinant of the metric can be modified, but never suppressed. Since the changes in the parameter imply changes in the dynamical variables, while the factor proportional to the momentum added to the evolution equation for the connection is unique, and so fixed, it is not clear whether this can be of help for improving numerical algorithms. We shall see this type of dependence arise in one of the developments of one of the above mentioned approaches.

In [29 ] a similar system, in the sense of using variables from the 3+1 decomposition, is obtained by imposing also the same generalized harmonic time gauge. This system, as is the original system of [18 ], is of higher order because it includes the electric and magnetic parts of the Weyl tensor in the 3+1 decomposition. As such, it contains more variables (fifty) than the two discussed above (thirty).