) is that it is hyperbolic for causal EOS [8
]. For hyperbolic systems
of conservation laws, the Jacobians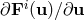 
have real eigenvalues and a complete set of eigenvectors
(see Section 9.3). Information about the solution propagates at finite velocities given by the eigenvalues of
the Jacobians. Hence, if the solution is known (in some spatial domain) at some given time, this fact can be
used to advance the solution to some later time (initial value problem). However, in general, it is not
possible to derive the exact solution for this problem. Instead one has to rely on numerical
methods which provide an approximation to the solution. Moreover, these numerical methods
must be able to handle discontinuous solutions, which are inherent to nonlinear hyperbolic
systems.
The simplest initial value problem with discontinuous data is called a Riemann problem, where the one-dimensional initial state consists of two constant states separated by a discontinuity. The majority of modern numerical methods, the so-called Godunov-type methods, are based on exact or approximate solutions of Riemann problems. Because of its theoretical and numerical importance, we discuss the solution of the special relativistic Riemann problem in the next Section 2.3.
 |
 |
 |
| http://www.livingreviews.org/lrr-2003-7 |
© Max Planck Society and the author(s)
Problems/comments to |