4.4 Realistic black holes
Thus a simple brane-based approach, while giving useful insights, does not lead to a realistic black hole
solution. There is no known solution representing a realistic black hole localized on the brane, which is
stable and without naked singularity. This remains a key open question of nonlinear brane-world gravity.
(Note that an exact solution is known for a black hole on a 1+2-brane in a 4D bulk [96], but this is a very
special case.) Given the nonlocal nature of  , it is possible that the process of gravitational collapse
itself leaves a signature in the black hole end-state, in contrast with general relativity and its no-hair
theorems. There are contradictory indications about the nature of the realistic black hole solution on the
brane:
, it is possible that the process of gravitational collapse
itself leaves a signature in the black hole end-state, in contrast with general relativity and its no-hair
theorems. There are contradictory indications about the nature of the realistic black hole solution on the
brane:
- Numerical simulations of highly relativistic static stars on the brane [319] indicate that general
relativity remains a good approximation.
- Exact analysis of Oppenheimer–Snyder collapse on the brane shows that the exterior is
non-static [110
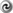 ], and this is extended to general collapse by arguments based on a generalized
AdS/CFT correspondence [94
], and this is extended to general collapse by arguments based on a generalized
AdS/CFT correspondence [94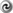 , 303
, 303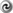 ].
].
The first result suggests that static black holes could exist as limits of increasingly compact static stars, but the
second result and conjecture suggest otherwise. This remains an open question. More recent numerical
evidence is also not conclusive, and it introduces further possible subtleties to do with the size of the black
hole [183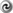 ].
].
On very small scales relative to the 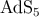 curvature scale,
curvature scale, 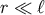 , the gravitational potential becomes
5D, as shown in Equation (40),
, the gravitational potential becomes
5D, as shown in Equation (40),
In this regime, the black hole is so small that it does not “see” the brane, so that it is approximately a 5D
Schwarzschild (static) solution. However, this is always an approximation because of the self-gravity of the
brane (the situation is different in ADD-type brane-worlds where there is no brane tension). As the black
hole size increases, the approximation breaks down. Nevertheless, one might expect that static solutions
exist on sufficiently small scales. Numerical investigations appear to confirm this [183]: Static metrics
satisfying the asymptotic 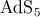 boundary conditions are found if the horizon is small compared to
boundary conditions are found if the horizon is small compared to  ,
but no numerical convergence can be achieved close to
,
but no numerical convergence can be achieved close to 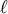 . The numerical instability that sets in may mask
the fact that even the very small black holes are not strictly static. Or it may be that there is a
transition from static to non-static behaviour. Or it may be that static black holes do exist on all
scales.
. The numerical instability that sets in may mask
the fact that even the very small black holes are not strictly static. Or it may be that there is a
transition from static to non-static behaviour. Or it may be that static black holes do exist on all
scales.
The 4D Schwarzschild metric cannot describe the final state of collapse, since it cannot incorporate the
5D behaviour of the gravitational potential in the strong-field regime (the metric is incompatible with
massive KK modes). A non-perturbative exterior solution should have nonzero 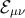 in order to be
compatible with massive KK modes in the strong-field regime. In the end-state of collapse, we expect an
in order to be
compatible with massive KK modes in the strong-field regime. In the end-state of collapse, we expect an
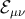 which goes to zero at large distances, recovering the Schwarzschild weak-field limit, but
which grows at short range. Furthermore,
which goes to zero at large distances, recovering the Schwarzschild weak-field limit, but
which grows at short range. Furthermore,  may carry a Weyl “fossil record” of the collapse
process.
may carry a Weyl “fossil record” of the collapse
process.
![]() ].
].
![]() curvature scale,
curvature scale, ![]() , the gravitational potential becomes
5D, as shown in Equation (40
, the gravitational potential becomes
5D, as shown in Equation (40![]() ),
), ![]() in order to be
compatible with massive KK modes in the strong-field regime. In the end-state of collapse, we expect an
in order to be
compatible with massive KK modes in the strong-field regime. In the end-state of collapse, we expect an
![]() which goes to zero at large distances, recovering the Schwarzschild weak-field limit, but
which grows at short range. Furthermore,
which goes to zero at large distances, recovering the Schwarzschild weak-field limit, but
which grows at short range. Furthermore, ![]() may carry a Weyl “fossil record” of the collapse
process.
may carry a Weyl “fossil record” of the collapse
process.