6.4 Curvature perturbations and the Sachs–Wolfe effect
The curvature perturbation 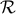 on uniform density surfaces is defined in Equation (267). The
associated gauge-invariant quantity
may be defined for matter on the brane. Similarly, for the Weyl “fluid” if
on uniform density surfaces is defined in Equation (267). The
associated gauge-invariant quantity
may be defined for matter on the brane. Similarly, for the Weyl “fluid” if 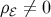 in the background, the
curvature perturbation on hypersurfaces of uniform dark energy density is
On large scales, the perturbed dark energy conservation equation is [191
in the background, the
curvature perturbation on hypersurfaces of uniform dark energy density is
On large scales, the perturbed dark energy conservation equation is [191 ]
which leads to
For adiabatic matter perturbations, by the perturbed matter energy conservation equation,
we find
This is independent of brane-world modifications to the field equations, since it depends on energy
conservation only. For the total, effective fluid, the curvature perturbation is defined as follows [191
]
which leads to
For adiabatic matter perturbations, by the perturbed matter energy conservation equation,
we find
This is independent of brane-world modifications to the field equations, since it depends on energy
conservation only. For the total, effective fluid, the curvature perturbation is defined as follows [191 ]: If
]: If
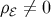 in the background, we have
and if
in the background, we have
and if 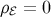 in the background, we get
where
in the background, we get
where 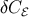 is a constant. It follows that the curvature perturbations on large scales, like the density
perturbations, can be found on the brane without solving for the bulk metric perturbations.
is a constant. It follows that the curvature perturbations on large scales, like the density
perturbations, can be found on the brane without solving for the bulk metric perturbations.
Note that  even for adiabatic matter perturbations; for example, if
even for adiabatic matter perturbations; for example, if 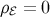 in the
background, then
in the
background, then
The KK effects on the brane contribute a non-adiabatic mode, although 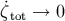 at low
energies.
at low
energies.
Although the density and curvature perturbations can be found on super-Hubble scales, the Sachs–Wolfe
effect requires 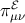 in order to translate from density/curvature to metric perturbations. In the 4D
longitudinal gauge of the metric perturbation formalism, the gauge-invariant curvature and metric
perturbations on large scales are related by
in order to translate from density/curvature to metric perturbations. In the 4D
longitudinal gauge of the metric perturbation formalism, the gauge-invariant curvature and metric
perturbations on large scales are related by
where the radiation anisotropic stress on large scales is neglected, as in general relativity, and 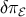 is the
scalar potential for
is the
scalar potential for 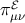 , equivalent to the covariant quantity
, equivalent to the covariant quantity 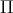 defined in Equation (289). In 4D
general relativity, the right hand side of Equation (319) is zero. The (non-integrated) Sachs–Wolfe formula
has the same form as in general relativity:
The brane-world corrections to the general relativistic Sachs–Wolfe effect are then given by [191]
where
defined in Equation (289). In 4D
general relativity, the right hand side of Equation (319) is zero. The (non-integrated) Sachs–Wolfe formula
has the same form as in general relativity:
The brane-world corrections to the general relativistic Sachs–Wolfe effect are then given by [191]
where 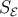 is the KK entropy perturbation (determined by
is the KK entropy perturbation (determined by  ). The KK term
). The KK term 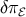 cannot be
determined by the 4D brane equations, so that
cannot be
determined by the 4D brane equations, so that 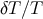 cannot be evaluated on large scales without solving
the 5D equations. (Equation (321) has been generalized to a 2-brane model, in which the radion makes a
contribution to the Sachs–Wolfe effect [176
cannot be evaluated on large scales without solving
the 5D equations. (Equation (321) has been generalized to a 2-brane model, in which the radion makes a
contribution to the Sachs–Wolfe effect [176 ].)
].)
The presence of the KK (Weyl, dark) component has essentially two possible effects:
- A contribution from the KK entropy perturbation
 that is similar to an extra isocurvature
contribution.
that is similar to an extra isocurvature
contribution.
- The KK anisotropic stress
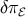 also contributes to the CMB anisotropies. In the absence
of anisotropic stresses, the curvature perturbation
also contributes to the CMB anisotropies. In the absence
of anisotropic stresses, the curvature perturbation 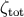 would be sufficient to determine the
metric perturbation
would be sufficient to determine the
metric perturbation 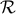 and hence the large-angle CMB anisotropies via Equations (318, 319,
320). However, bulk gravitons generate anisotropic stresses which, although they do not affect
the large-scale curvature perturbation
and hence the large-angle CMB anisotropies via Equations (318, 319,
320). However, bulk gravitons generate anisotropic stresses which, although they do not affect
the large-scale curvature perturbation  , can affect the relation between
, can affect the relation between 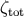 ,
, 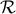 , and
, and
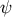 , and hence can affect the CMB anisotropies at large angles.
, and hence can affect the CMB anisotropies at large angles.
A simple phenomenological approximation to 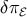 on large scales is discussed in [19], and the
Sachs–Wolfe effect is estimated as
on large scales is discussed in [19], and the
Sachs–Wolfe effect is estimated as
where 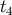 is the 4D Planck time, and
is the 4D Planck time, and 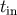 is the time when the KK anisotropic stress is induced on the
brane, which is expected to be of the order of the 5D Planck time.
is the time when the KK anisotropic stress is induced on the
brane, which is expected to be of the order of the 5D Planck time.
A self-consistent approximation is developed in [177 ], using the low-energy 2-brane
approximation [290
], using the low-energy 2-brane
approximation [290 , 298
, 298 , 299
, 299 , 300
, 300 , 320
, 320 ] to find an effective 4D form for
] to find an effective 4D form for 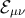 and hence for
and hence for 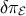 . This is
discussed below.
. This is
discussed below.
![]() even for adiabatic matter perturbations; for example, if
even for adiabatic matter perturbations; for example, if ![]() in the
background, then
in the
background, then ![]() in order to translate from density/curvature to metric perturbations. In the 4D
longitudinal gauge of the metric perturbation formalism, the gauge-invariant curvature and metric
perturbations on large scales are related by
in order to translate from density/curvature to metric perturbations. In the 4D
longitudinal gauge of the metric perturbation formalism, the gauge-invariant curvature and metric
perturbations on large scales are related by ![]() on large scales is discussed in [19], and the
Sachs–Wolfe effect is estimated as
on large scales is discussed in [19], and the
Sachs–Wolfe effect is estimated as ![]() ], using the low-energy 2-brane
approximation [290
], using the low-energy 2-brane
approximation [290![]() , 298
, 298![]() , 299
, 299![]() , 300
, 300![]() , 320
, 320![]() ] to find an effective 4D form for
] to find an effective 4D form for ![]() and hence for
and hence for ![]() . This is
discussed below.
. This is
discussed below.