6.3 Density perturbations on large scales
In the covariant approach, we define matter density and expansion (velocity) perturbation scalars, as in
4D general relativity,
Then we can define dimensionless KK perturbation scalars [218 ],
where the scalar potentials
],
where the scalar potentials 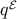 and
and  are defined by Equations (251, 252). The KK energy density
(dark radiation) produces a scalar fluctuation
are defined by Equations (251, 252). The KK energy density
(dark radiation) produces a scalar fluctuation 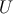 which is present even if
which is present even if 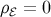 in the background, and
which leads to a non-adiabatic (or isocurvature) mode, even when the matter perturbations
are assumed adiabatic [122
in the background, and
which leads to a non-adiabatic (or isocurvature) mode, even when the matter perturbations
are assumed adiabatic [122 ]. We define the total effective dimensionless entropy
]. We define the total effective dimensionless entropy 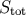 via
where
via
where  is given in Equation (103). Then
is given in Equation (103). Then
If  in the background, then
in the background, then  is an isocurvature mode:
is an isocurvature mode: 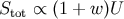 . This isocurvature
mode is suppressed during slow-roll inflation, when
. This isocurvature
mode is suppressed during slow-roll inflation, when 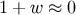 .
.
If 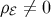 in the background, then the weighted difference between
in the background, then the weighted difference between 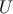 and
and 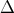 determines the
isocurvature mode:
determines the
isocurvature mode:  . At very high energies,
. At very high energies,  , the entropy is
suppressed by the factor
, the entropy is
suppressed by the factor 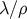 .
.
The density perturbation equations on the brane are derived by taking the spatial gradients of
Equations (253), (255), and (257), and using Equations (254) and (256). This leads to [122 ]
]
The KK anisotropic stress term  occurs only via its Laplacian,
occurs only via its Laplacian, 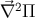 . If we can neglect this term on
large scales, then the system of density perturbation equations closes on super-Hubble scales [218]. An
equivalent statement applies to the large-scale curvature perturbations [191
. If we can neglect this term on
large scales, then the system of density perturbation equations closes on super-Hubble scales [218]. An
equivalent statement applies to the large-scale curvature perturbations [191 ]. KK effects then introduce two
new isocurvature modes on large scales (associated with
]. KK effects then introduce two
new isocurvature modes on large scales (associated with  and
and 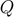 ), and they modify the evolution of
the adiabatic modes as well [122
), and they modify the evolution of
the adiabatic modes as well [122 , 201
, 201 ].
].
Thus on large scales the system of brane equations is closed, and we can determine the density
perturbations without solving for the bulk metric perturbations.
We can simplify the system as follows. The 3-Ricci tensor defined in Equation (134) leads to a scalar
covariant curvature perturbation variable,
It follows that 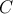 is locally conserved (along
is locally conserved (along  flow lines):
We can further simplify the system of equations via the variable
This should not be confused with the Bardeen metric perturbation variable
flow lines):
We can further simplify the system of equations via the variable
This should not be confused with the Bardeen metric perturbation variable  , although it is the
covariant analogue of
, although it is the
covariant analogue of  in the general relativity limit. In the brane-world, high-energy and KK effects
mean that
in the general relativity limit. In the brane-world, high-energy and KK effects
mean that  is a complicated generalization of this expression [201
is a complicated generalization of this expression [201 ] involving
] involving 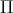 , but the simple
, but the simple 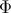 above is still useful to simplify the system of equations. Using these new variables, we find the closed system
for large-scale perturbations:
If there is no dark radiation in the background,
above is still useful to simplify the system of equations. Using these new variables, we find the closed system
for large-scale perturbations:
If there is no dark radiation in the background,  , then
and the above system reduces to a single equation for
, then
and the above system reduces to a single equation for  . At low energies, and for constant
. At low energies, and for constant  , the
non-decaying attractor is the general relativity solution,
At very high energies, for
, the
non-decaying attractor is the general relativity solution,
At very high energies, for 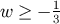 , we get
where
, we get
where 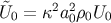 , so that the isocurvature mode has an influence on
, so that the isocurvature mode has an influence on  . Initially,
. Initially,  is suppressed
by the factor
is suppressed
by the factor 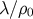 , but then it grows, eventually reaching the attractor value in Equation (302).
For slow-roll inflation, when
, but then it grows, eventually reaching the attractor value in Equation (302).
For slow-roll inflation, when  , with
, with  and
and  , we get
where
, we get
where 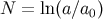 , so that
, so that  has a growing-mode in the early universe. This is different from general
relativity, where
has a growing-mode in the early universe. This is different from general
relativity, where  is constant during slow-roll inflation. Thus more amplification of
is constant during slow-roll inflation. Thus more amplification of 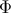 can be achieved
than in general relativity, as discussed above. This is illustrated for a toy model of inflation-to-radiation in
Figure 8. The early (growing) and late time (constant) attractor solutions are seen explicitly in the
plots.
can be achieved
than in general relativity, as discussed above. This is illustrated for a toy model of inflation-to-radiation in
Figure 8. The early (growing) and late time (constant) attractor solutions are seen explicitly in the
plots.
The presence of dark radiation in the background introduces new features. In the radiation era
(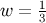 ), the non-decaying low-energy attractor becomes [131]
), the non-decaying low-energy attractor becomes [131]
The dark radiation serves to reduce the final value of  , leaving an imprint on
, leaving an imprint on  , unlike the
, unlike the 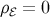 case, Equation (302). In the very high energy limit,
Thus
case, Equation (302). In the very high energy limit,
Thus 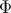 is initially suppressed, then begins to grow, as in the no-dark-radiation case, eventually reaching
an attractor which is less than the no-dark-radiation attractor. This is confirmed by the numerical
integration shown in Figure 9.
is initially suppressed, then begins to grow, as in the no-dark-radiation case, eventually reaching
an attractor which is less than the no-dark-radiation attractor. This is confirmed by the numerical
integration shown in Figure 9.
![]() in the background, then
in the background, then ![]() is an isocurvature mode:
is an isocurvature mode: ![]() . This isocurvature
mode is suppressed during slow-roll inflation, when
. This isocurvature
mode is suppressed during slow-roll inflation, when ![]() .
.
![]() in the background, then the weighted difference between
in the background, then the weighted difference between ![]() and
and ![]() determines the
isocurvature mode:
determines the
isocurvature mode: ![]() . At very high energies,
. At very high energies, ![]() , the entropy is
suppressed by the factor
, the entropy is
suppressed by the factor ![]() .
.
![]() ), (255
), (255![]() ), and (257
), and (257![]() ), and using Equations (254
), and using Equations (254![]() ) and (256
) and (256![]() ). This leads to [122
). This leads to [122![]() ]
]
![]() ) leads to a scalar
covariant curvature perturbation variable,
) leads to a scalar
covariant curvature perturbation variable, ![]() ), the non-decaying low-energy attractor becomes [131]
), the non-decaying low-energy attractor becomes [131]