The Development of Loop Gravity

3 The Development of Loop Gravity

The following chronology does not exhaust the history of loop gravity, it only indicates some steps in the construction of the theory, in order to provide orientation.

1986: Connection formulation of general relativity
Loop gravity is based on the “Ashtekar formulation” of classical general relativity. (Abhay Ashtekar calls it “connectio-dynamics”, in contrast to Wheeler’s “geometro-dynamics”.) [271 , 16 , 17 ]. Many recent works in loop gravity are based on a real variant of the original Ashtekar connection whose utility for Lorentzian general relativity has been emphasized by Barbero [60 , 61 , 62 , 63 ].
1986: Wilson-loop solutions of the Hamiltonian constraint
Soon after the introduction of the Ashtekar variables, Ted Jacobson and Lee Smolin realize that the Wheeler–DeWitt equation, reformulated in terms of the new variables, admits a simple class of exact solutions: the traces of the holonomies of the Ashtekar connection around smooth non-self-intersecting loops [161 ]. In other words: the Wilson loops of the Ashtekar connection solve the Wheeler–DeWitt equation if the loops are smooth and non self-intersecting.
1987: The loop representation
The discovery of the Jacobson–Smolin Wilson-loop solutions suggests that one “change basis in the Hilbert space of the theory”, choosing the Wilson loops as the new basis states for quantum gravity [264 , 240 , 263 , 265 ]. Quantum states can be represented in terms of their expansion on the loop basis, namely as functions on a space of loops. This idea is well known in the context of canonical lattice Yang–Mills theory [164 ]. Its application to continuous Yang–Mills theory had been explored by Gambini and Trias [132 , 133 ]. The difficulties of the loop representation in the context of Yang–Mills theory are cured by the diffeomorphism invariance of GR (see Section 6.4). The immediate results are two: (i) the diffeomorphism constraint is completely solved by knot states (loop functionals that depend only on the knotting of the loops), making earlier suggestions by Smolin on the role of knot theory in quantum gravity [273 ] concrete; and (ii) knot states with support on non-self-intersecting loops are proven to be solutions of all quantum constraints, namely exact physical states of quantum gravity.
1988: Exact states of quantum gravity
The investigation of exact solutions of the quantum constraint equations, and their relation to knot theory (in particular to the Jones polynomial and other knot invariants), started soon after the formulation of the theory [149 , 78 , 79 , 80 , 81 , 233 , 127 , 129 , 163 , 122 , 107 ].
1989: Model theories
The years immediately following the discovery of the loop formalism are mostly dedicated to understanding the loop representation by studying it in simpler contexts, such as 2+1 general relativity [26 , 195 , 36 ], Maxwell [37 ], linearized gravity [38 ], and, later, 2D Yang–Mills theory [35 ].
1992: Discreteness: I. Weaves
The first indication that the theory predicts Planck-scale discreteness derives from studying the states that approximate flat geometries on large scale [39 ]. These states, called “weaves”, can be viewed as a formalization of Wheeler’s “spacetime foam”. Surprisingly, these states turn out not to require that the average spacing of the loops go to zero.
1992: $∗ C$ algebraic framework
Abhay Ashtekar and Chris Isham show that the loop transform can be given a rigorous mathematical foundation, and lay the foundation for a mathematical systematization of the loop ideas, based on 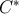$C ∗$ algebra ideas [27 ].
1994: Fermions
Fermion coupling is explored in [206 , 207 ]. Later, matter’s kinematics is studied by Baez and Krasnov [168 , 54 ], while Thiemann extends his results on dynamics to the coupled Einstein Yang–Mills system in [290 ].
1994: Ashtekar–Lewandowski measure and scalar product
Abhay Ashtekar and Jerzy Lewandowski lay the foundation of the differential formulation of loop quantum gravity by constructing a diffeomorphism-invariant measure on the space of (generalized) connections [28 , 29 , 30 ]. They give a mathematically-rigorous construction of the state space of the theory. They define a consistent scalar product and prove that the quantum operators in the theory are consistently defined. Key contributions to the understanding of the measure are given by John Baez, Don Marolf and Josè Mourão [43 , 44 , 42 , 198 ]. Don Marolf clarifies the use of formal group integration for solving the constraints [194 , 196 , 197 ]. The definitive setting of the two versions of the formalism is completed shortly after for the loop formalism (the actual loop representation) [98 ] and for the differential formalism (the connection representation) [34 ]. Roberto DePietri proves the equivalence of the two formalisms [96 ], using ideas from Thiemann [284 ] and Lewandowski [175 ].
1994: Discreteness: II. Area and volume eigenvalues
Certain geometrical quantities, in particular area and volume, are represented by operators that have discrete eigenvalues. The first set of these eigenvalues is obtained in [268 ]. The result is confirmed and extended using a number of different techniques. Renate Loll [183 , 184 ] uses lattice techniques to analyze the volume operator and correct a numerical error in [268 ]. Ashtekar and Lewandowski [174 , 31 ] recover and complete the computation of the spectrum of the area using the connection representation and new regularization techniques. In turn, the full spectrum of the area is then recovered using the loop representation [121 ]. The general eigenvalues of the volume are computed [98 ]. Lewandowski clarifies the relation between different versions of the volume operator [175 ].
1995: Spin networks
A long standing problem with the loop basis was its overcompleteness. A technical, but crucial step in understanding the theory is the discovery of the spin-network basis, which solves this overcompleteness [269 ]. The idea derives from the work of Roger Penrose [224 , 223 ], from analogous bases used in lattice gauge theory, and from ideas by Lewandowski [173 ] and Jorge Pullin on the relevance of graphs and nodes for the theory. The spin network formalism is cleaned up and clarified by John Baez [47 , 48 ].
1996: Hamiltonian constraint
The first version of the loop Hamiltonian constraint [263 , 265 ] is studied and repeatedly modified in a number of works [149 , 71 , 81 , 79 , 78 , 80 , 233 , 127 , 74 ]. A key step is the realization that certain regularized loop operators have finite limits on diffeomorphism-invariant states [266 ]. The search culminates with the work of Thomas Thiemann, who is able to construct a fully well-defined anomaly-free Hamiltonian operator [285 , 289 , 291 ].
1996: Black-hole entropy
The derivation of the Bekenstein–Hawking formula for the entropy of a black hole from loop quantum gravity is obtained [253 ], on the basis of the ideas of Kirill Krasnov [170 , 171 ] and Lee Smolin [274 ]. The theory is developed and made rigorous by Ashtekar, Baez, Corichi and Krasnov [22 ].
1997: Spin foams
A “sum over histories” spacetime formulation of loop quantum gravity is derived [257 , 236 ] from the canonical theory. The resulting covariant theory turns out to be a sum over topologically non-equivalent surfaces, realizing suggestions by Baez [45 , 42 , 47 , 41 ], Reisenberger [235 , 234 ] and Iwasaki [156 ] that a covariant version of loop gravity should look like a theory of surfaces. Baez studies the general structure of theories defined in this manner [49 ] and introduces the term “spin foam”.
1997: The Barrett–Crane vertex
John Barrett and Louis Crane introduce the Barrett–Crane vertex amplitude [66 ], which will become one of the main tools for exploring dynamics in loop gravity and in other approaches.
1999: Group field theory
The definition of the Barrett–Crane spin-foam model – in its different versions – is completed in [97 , 115 ], where group-field-theory techniques are also introduced, deriving them from topological field theories.
2000: Quantum cosmology
The application of loop quantum gravity to cosmology is started by Martin Bojowald [72 ], to be later extensively developed by Ashtekar, Bojowald and others.
2001: Spin-foam finiteness
Alejandro Perez gives the first proof of finiteness of a spin-foam model [228 ].
2003: Master constraint
Thomas Thiemann introduces the idea of replacing the full set of quantum constraints with a single (“master”) constraint [293 ].
2004: Black hole singularity at r = 0
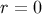Leonardo Modesto [203 ], and, independently, Ashtekar and Bojowald [24 ], apply techniques derived from quantum cosmology to explore the $r = 0$ singularity at the center of a black hole, showing that this is controlled by the quantum theory.
2005: Loop/spin-foam equivalence in 3D
Karim Noui and Alejandro Perez prove the equivalence of loop quantum gravity and the spin-foam formalism in three-dimensional quantum gravity [210 ].
2005: The LOST theorem
A key uniqueness theorem for the representation used in loop quantum gravity is proved by Lewandowski, Okolow, Sahlmann and Thiemann [176 ] and, independently and in a slightly different version, by Christian Fleischhack [111 ].
2005: Noncommutative geometry from loop quantum gravity
Laurent Freidel and Etera Livine show that the low-energy limit of quantum gravity coupled with matter in three dimensions is equivalent to a field theory on a noncommutative spacetime [116 ].
2006: Graviton propagator
Beginning of the computation of n-point functions from loop quantum gravity [205 ] and first computation of some components of the graviton propagator [262 ].
2007: The new vertex and the loop/spin-foam relation in 4D
A vertex amplitude correcting some difficulties of the Barrett–Crane model is introduced in [106 ], and gives rise to rapid development [105 , 181 , 182 , 227 ] leading to the formulation of a class of spin-foam models that provide a covariant definition of the LQG dynamics [104 , 114 , 6 ].