5 Discussion
After the explicit examples in Sections 3 and 4, here we will collect some general considerations.One noteworthy remark for models with a minimal length scale is that discreteness seems neither necessary nor sufficient for the existence of a minimal length scale. String theory is an example that documents that discreteness is not necessary for a limit to the resolution of structures, and [60] offered example in which discreteness does not put a finite limit on the resolution of spatial distances (though the physical interpretation, or the observability of these quantities requires more study).
We have also seen that the minimal length scale is not necessarily the Planck length. In string theory, it is naturally the string scale that comes into play, or a product of the string coupling and the string scale if one takes into account D-branes. Also in ASG, or emergent gravity scenarios, the Planck mass might just appear as a coupling constant in some effective limit, while fundamentally some other constant is relevant. We usually talk about the Planck mass because we know of no higher energy scale that is relevant to the physics we know, so it is the obvious candidate, but not necessarily the right one.
5.1 Interrelations
The previously-discussed theories and models are related in various ways. We had already mentioned that the path-integral duality (Section 4.7) is possibly related to T-duality (Section 3.2.4) or conformal fluctuations in quantum gravity (Section 3.4), and that string theory is one of the reasons to study non-commutative geometries. In addition to this, it has also been argued that the coherent-state approach to non-commutative geometries represents another model for minimal length modified quantum mechanics [293]. The physics of black holes in light of the coherent state approach has been reviewed in [239].
DSR has been motivated by LQG, though no rigorous derivation exists to date. However,
there are non-rigorous arguments that DSR may emerge from a semiclassical limit of quantum
gravity theories in the form of an effective field theory with an energy dependent metric [29], or
that DSR (in form of a  -Poincaré algebra) may result from a version of path integral
quantization [198]. In addition, it has been shown that in 2+1 dimensional gravity coupled to matter, the
gravitational degrees of freedom can be integrated out, leaving an effective field theory for the
matter, which is a quantum field theory on
-Poincaré algebra) may result from a version of path integral
quantization [198]. In addition, it has been shown that in 2+1 dimensional gravity coupled to matter, the
gravitational degrees of freedom can be integrated out, leaving an effective field theory for the
matter, which is a quantum field theory on  -Minkowski spacetime, realizing a particular
version of DSR [114]. Recently, it has also been suggested that DSR could arise via LQC [59].
-Minkowski spacetime, realizing a particular
version of DSR [114]. Recently, it has also been suggested that DSR could arise via LQC [59].
As already mentioned, it has been argued in [74] that ASG may give rise to DSR if one carefully identifies the momentum and the pseudo-momentum. In [133] how the running of the Planck’s mass can give rise to a modified dispersion relation was studied.
5.2 Observable consequences
The most relevant aspect of any model is to make contact with phenomenology. We have mentioned a few phenomenological consequences that are currently under study, but for completeness we summarize them here.
To begin with, experimental evidence that speaks for any one of the approaches to quantum gravity discussed in Section 3 will also shed light on the nature of a fundamental length scale. Currently, the most promising areas to look for such evidence are cosmology (in particular the polarization of the cosmic microwave background) and miscellaneous signatures of Lorentz-invariance violation. The general experimental possibilities to make headway on a theory of quantum gravity have been reviewed in [19*, 164]. One notable recent development, which is especially interesting for the question of a minimal length scale, is the possibility that direct evidence for the discrete nature of spacetime may be found in the emission spectra of primordial black holes, if such black holes exist and can be observed [50].
Signatures directly related to the minimal length proposal are a transplanckian cut-off that would
make itself noticeable in the cosmic microwave background in the way that the spectrum of
fluctuations would not be exactly scale invariant [220, 68]. Imprints from scalar and tensor
perturbations have been studied in [37, 38, 36], and in [88, 89] it has been argued in that
observable consequences arise at the level of the CMB bispectrum. Deformations of special
relativity can lead to an energy-dependent dispersion, which might be an observable effect
for photons reaching Earth from 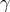 -ray bursts at high redshift [26, 19, 20]. Minimal length
deformations do, in principle, give rise to computable correction terms to a large number of quantum
mechanical phenomena (see Section 4.3.2). This allows one to put bounds on the parameters of the
model. These bounds are presently many orders of magnitude away from the regime where
one would naturally expect quantum gravitational effects. While it is therefore unlikely that
evidence for a minimal length can be found in these experiments, it should be kept in mind
that we do not strictly speaking know that the minimal length scale is identical to the Planck
scale and not lower, and scientific care demands that every new range of parameter space be
scrutinized.
-ray bursts at high redshift [26, 19, 20]. Minimal length
deformations do, in principle, give rise to computable correction terms to a large number of quantum
mechanical phenomena (see Section 4.3.2). This allows one to put bounds on the parameters of the
model. These bounds are presently many orders of magnitude away from the regime where
one would naturally expect quantum gravitational effects. While it is therefore unlikely that
evidence for a minimal length can be found in these experiments, it should be kept in mind
that we do not strictly speaking know that the minimal length scale is identical to the Planck
scale and not lower, and scientific care demands that every new range of parameter space be
scrutinized.
Recently, it was proposed that a massive quantum mechanical oscillator might allow one to test Planck-scale physics [264] in a parameter range close to the Planck scale. This proposal should be regarded with caution because the deformations for composite systems used therein do not actually follow from the ones that were motivated by our considerations in Section 3, because the massive oscillator represents a multi-particle state. If one takes into account the ad-hoc solutions to the soccer-ball problem, that are necessary for consistency of the theory when considering multi-particle states (see Section 4.2.4), then the expected effect is suppressed by a mass many orders of magnitude above the Planck mass. Thus, it is unlikely that the proposed experiment will be sensitive to Planck-scale physics.
It is clearly desireable to be able to study composite systems and ensembles, which would allow us to make use of recent advances in quantum optics and data from the early high-density era of the universe. Thus, solving the soccer-ball problem is of central relevance for making contact between these models and phenomenology.
5.3 Is it possible that there is no minimal length?
“The last function of reason is to recognize that there are an infinity of things which surpass it.”
– Blaise Pascal
After having summarized all the motivations for the existence of a minimal length scale, we have to take care that our desire for harmony does not have us neglecting evidence to the contrary.
We have already discussed that there are various possibilities for a minimal length scale to make itself noticeable, and this does not necessarily mean that it appears as a lower bound on the spatial resolution. We could instead merely have a bound on products of spatial and temporal extensions. So in this sense there might not be a minimal length, just a minimal length scale. Therefore, we answer the question posed in this section’s title in the affirmative. Let us then ask if it is possible that there is no minimal length scale.
The case for a minimal length scale seems clear in string theory and LQG, but it is less clear in emergent gravity scenarios. If gravity is emergent, and the Planck mass appears merely as a coupling constant in the effective limit, this raises the question, of there is some way in which the fundamental theory cannot have a limiting value at all.
In ASG, the arguments we have reviewed in Section 3.5 are suggestive but not entirely conclusive. The supporting evidence that we discussed comes from graviton scattering, and from a study of a particular type of Euclidean quantum spacetimes.13 Notwithstanding the question of whether general relativity actually has a (physically-meaningful) fixed point, the evidence for a minimal length is counterintuitive even in ASG, because gravity becomes weaker at high energies, so, naively, one would expect its distorting effects to also become weaker.
As Mead carefully pointed out in his article investigating the Heisenberg microscope with gravity:
“We have also neglected the effect of quantum fluctuations in the gravitational field. However, these would be expected to provide an additional source of uncertainty, not remove those already present. Hence, inclusion of this effect would, if anything, strengthen the result.” ([222], p. B855)
That is correct, one might add, unless gravity itself weakens and counteracts the effect of the quantum fluctuations. In fact, in [51] the validity of the Hoop conjecture in a thought experiment testing short-distance structures has been re-examined in the context of ASG. It was found that the running of the Planck mass avoids the necessity of forming a trapped surface at the scale of the experiment. However, it was also found that still no information about the local physics can be transmitted to an observer in the asymptotic distance.
As previously mentioned, there is also no obvious reason for the existence of a minimal length scale in discrete approaches where the lattice spacing is taken to zero [13]. To study the question, one needs to investigate the behavior of suitably constructed observables in this limit. We also note the central role of the Hoop conjecture for our arguments, and that it is, for general configurations, an unproven conjecture.
These questions are presently very much under discussion; we mention them to show that the case is not as settled as it might have seemed from Sections 3 and 4.