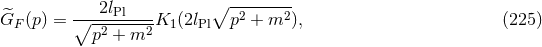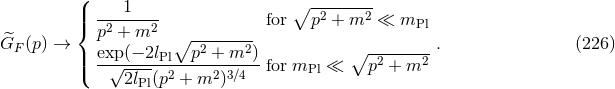4 Models and Applications
In this section we will investigate some models that have been developed to deal with a minimal length or, more often, a maximum energy scale. The models discussed in the following are not in themselves approaches to a fundamental description of spacetime like the ones previously discussed that lead us to seriously consider a finite resolution of structures. Instead, the models discussed in this section are attempts to incorporate the notion of a minimal length into the standard model of particle physics and/or general relativity by means of a modification of quantum mechanics, quantum field theory and Poincaré symmetry. These models are meant to provide an effective description of the possible effects of a minimal length with the intention to make contact with phenomenology and thereby ideally constrain the possible modifications.10As mentioned previously, the non-commutative geometries discussed in Section 3.6 could also have rightfully claimed a place in this section on models and applications.
Before we turn towards the implementation, let us spend some words on the interpretation because the construction of a suitable model depends on the physical picture one aims to realize.
4.1 Interpretation of a minimal length scale
It is the central premise of this review that there exists a minimal length scale that plays a fundamental role in the laws of nature. In the discussion in Section 5 we will consider the possibility that this premise is not fulfilled, but for now we try to incorporate a minimal length scale into the physical description of the world. There are then still different ways to think about a minimal length scale or a maximum energy scale.
One perspective that has been put forward in the literature [14, 193, 15, 212*] is that for the Planck mass to be observer independent it should be invariant under Lorentz boosts. Since normal Lorentz boosts do not allow this, the observer independence of the Planck mass is taken as a motivation to modify special relativity to what has become known as ‘Deformed Special Relativity’ (DSR). (See also Section 4.5). In brief, this modification of special relativity allows one to perform a Lorentz boost on momentum space in such a way that an energy of Planck mass remains invariant.
While that is a plausible motivation to look into such departures from special relativity, one has to keep
in mind that just because a quantity is of dimension length (mass) it must not necessarily transform under
Lorentz boosts as a spatial or time-like component of a spacetime (or momentum) four vector. A constant of
dimension length can be invariant under normal Lorentz boosts, for example, if it is a spacetime (proper)
distance. This interpretation is an essential ingredient to Padmanabhan’s path integral approach
(see Section 4.7). Another example is the actual mass of a particle, which is invariant under
Lorentz boosts by merit of being a scalar. Thinking back to our historical introduction, we
recall that the coupling constant of Fermi’s theory for the weak interaction is proportional to
the inverse of the 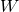 -mass and therefore observer independent in the sense that it does not
depend on the rest frame in which we determine it – and that without the need to modify special
relativity.
-mass and therefore observer independent in the sense that it does not
depend on the rest frame in which we determine it – and that without the need to modify special
relativity.
Note also that coupling constants do depend on the energy with which structures are probed, as discussed in Section 3.5 on ASG. There we have yet another interpretation for a minimal length scale, that being the energy range (in terms of normally Lorentz-invariant Mandelstam variables for the asymptotically in/out-going states) where the running Planck mass comes into the fixed-point regime. The center-of-mass energy corresponding to the turning point of the total cross section in graviton scattering, for example, makes it a clean and observer-independent definition of an energy scale, beyond which there is no more new structure to be found.
One should also keep in mind that the outcome of a Lorentz boost is not an observable per se. To actually determine a distance in some reference frame one has to perform a measurement. Thus, for the observer independence of a minimal length, it is sufficient if there is no operational procedure that allows one to resolve structures to a precision better than the Planck length. It has been argued in [154] that this does not necessitate a modification of Lorentz boosts for the momenta of free particles; it is sufficient if the interactions of particles do not allow one to resolve structures beyond the Planck scale. There are different ways this could be realized, for example, by an off-shell modification of the propagator that prevents arbitrarily-high momentum transfer. As previously discussed, there are some indications that ASG might realize such a feature and it can, in a restricted sense, be interpreted as a version of DSR [74*].
An entirely different possibility that we mentioned in Section 3.7, has recently been put forward in [106, 105], where it was argued that it is exactly because of the universality of black-hole production that the Planck length already plays a fundamental role in classical gravity and there is no need to complete the theory in the high energy range.
4.2 Modified commutation relations
The most widely pursued approach to model the effects of a minimal length scale in quantum mechanics and quantum field theory is to reproduce the GUP starting from a modified commutation relation for position and momentum operators. This modification may or may not come with a modification also of the commutators of these operators with each other, which would mean that the geometry in position or momentum space becomes non-commuting.
The modified commutation relations imply not only a GUP, but also a modified dispersion relation and a modified Poincaré-symmetry in momentum and/or position space. The literature on the subject is vast, but the picture is still incomplete and under construction.
4.2.1 Recovering the minimal length from modified commutation relations
To see the general idea, let us start with a simple example that shows the relation of modified commutation
relations to the minimal length scale. Consider variables 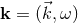 , where
, where 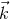 is the three vector,
components of which will be labeled with small Latin indices, and
is the three vector,
components of which will be labeled with small Latin indices, and 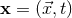 . Under quantization, the
associated operators obey the standard commutation relations
. Under quantization, the
associated operators obey the standard commutation relations
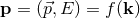 , where
, where 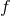 is an injective function, so that
is an injective function, so that
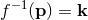 is well defined. We will also use the notation
is well defined. We will also use the notation 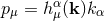 with the inverse
with the inverse
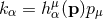 . For the variables
. For the variables 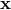 and
and 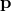 one then has the commutation relations
If one now looks at the uncertainty relation between
one then has the commutation relations
If one now looks at the uncertainty relation between 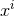 and
and 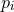 , one finds
To be concrete, let us insert some function, for example a generic expansion of the form
, one finds
To be concrete, let us insert some function, for example a generic expansion of the form 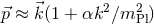 plus higher orders in
plus higher orders in 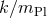 , so that the inverse relation is
, so that the inverse relation is 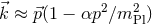 . Here,
. Here, 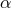 is some
dimensionless parameter. One then has
Since this function is convex, we can rewrite the expectation value in (176*) to
And inserting the expression for the variance
is some
dimensionless parameter. One then has
Since this function is convex, we can rewrite the expectation value in (176*) to
And inserting the expression for the variance 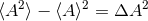 , one obtains
or
Thus, we have reproduced the GUP that we found in the thought experiments in Section 3.1 with a
minimal possible uncertainty for the position [175*, 26*, 207, 209, 25].
, one obtains
or
Thus, we have reproduced the GUP that we found in the thought experiments in Section 3.1 with a
minimal possible uncertainty for the position [175*, 26*, 207, 209, 25].
However, though the nomenclature here is deliberately suggestive, one has to be careful with
interpreting this finding. What the inequality (180*) tells us is that we cannot measure the position to
arbitrary precision if we do it by varying the uncertainty in  . That has an operational meaning
only if we assign to
. That has an operational meaning
only if we assign to 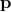 the meaning of a physical momentum, in particular it should be a
Hermitian operator. To distinguish between the physical quantity
the meaning of a physical momentum, in particular it should be a
Hermitian operator. To distinguish between the physical quantity 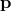 , and
, and 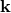 that fulfills the
canonical commutation relations, the
that fulfills the
canonical commutation relations, the 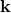 is sometimes referred to as the ‘pseudo-momentum’ or,
because it is conjugated to
is sometimes referred to as the ‘pseudo-momentum’ or,
because it is conjugated to 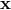 , as ‘the wave vector.’ One can then physically interpret the
non-linear relation between
, as ‘the wave vector.’ One can then physically interpret the
non-linear relation between 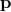 and
and 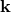 as an energy dependence of Planck’s constant [156*].
as an energy dependence of Planck’s constant [156*].
To further clarify this, let us turn towards the question of Lorentz invariance. If we do not make statements in addition to the commutation relations, we do not know anything about the transformation behavior of the quantities. For all we know, they could have an arbitrary transformation behavior and Lorentz invariance could just be broken. If we require Lorentz invariance to be preserved, this opens the question of how it is preserved, what is the geometry of its phase space, and what is its Poisson structure. And, most importantly, how do we identify physically-meaningful coordinates on that space?
At the time of writing, no agreed upon picture has emerged. Normally, phase space is the cotangential bundle of the spacetime manifold. One might generalize this to a bundle of curved momentum spaces, an idea that dates back at least to Max Born in 1938 [64]. In a more radical recent approach, the ‘principle of relative locality’ [287*, 286*, 169*, 27*, 23*, 21*] phase space is instead considered to be the cotangential bundle of momentum space.
To close this gap in our example, let us add some more structure and assume that the phase space is a
trivial bundle 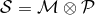 , where
, where 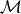 is spacetime and
is spacetime and 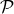 is momentum space. Elements of this space
have the form
is momentum space. Elements of this space
have the form 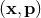 . If we add that the quantity
. If we add that the quantity 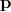 is a coordinate on
is a coordinate on 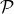 and transforms
according to normal Lorentz transformations under a change of inertial frames, and
and transforms
according to normal Lorentz transformations under a change of inertial frames, and 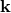 is another
coordinate system, then we know right away how
is another
coordinate system, then we know right away how 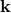 transforms because we can express it by use of
the function
transforms because we can express it by use of
the function 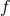 . If we do a Lorentz transformation on
. If we do a Lorentz transformation on 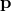 , so that
, so that 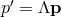 , then we have
, then we have
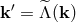 . In particular, one can
chose
. In particular, one can
chose 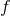 in such a way that it maps an infinite value of
in such a way that it maps an infinite value of 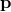 (in either the spatial or temporal entries, or
both) to a finite value of
(in either the spatial or temporal entries, or
both) to a finite value of 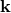 at the Planck energy. The so-constructed Lorentz transformation on
at the Planck energy. The so-constructed Lorentz transformation on 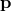 will
then keep the Planck scale invariant, importantly without introducing any preferred frame. This is the
basic idea of deformations of special relativity, some explicit examples of which we will meet in
Section 4.5.
will
then keep the Planck scale invariant, importantly without introducing any preferred frame. This is the
basic idea of deformations of special relativity, some explicit examples of which we will meet in
Section 4.5.
If one assumes that 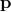 transforms as a normal Lorentz vector, one has
transforms as a normal Lorentz vector, one has
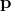 , one readily finds
which gives us the infinitesimal version of (181*) by help of the usual expansion
where
, one readily finds
which gives us the infinitesimal version of (181*) by help of the usual expansion
where 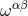 are the group parameters of
are the group parameters of 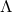 .
.
Now that we know how 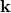 transforms, we still need to add information for how the coordinates on
transforms, we still need to add information for how the coordinates on 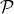 are supposed to be matched to those on
are supposed to be matched to those on 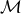 . One requirement that we can use to select a basis on
. One requirement that we can use to select a basis on 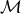 along with that on
along with that on 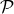 under a Lorentz transformation is that the canonical form of the commutation
relations should remain preserved. With this requirement, one then finds for the infinitesimal transformation
of
under a Lorentz transformation is that the canonical form of the commutation
relations should remain preserved. With this requirement, one then finds for the infinitesimal transformation
of 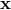 [253]
[253]
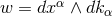 canonical.
canonical.
A word of caution is in order here because the innocent looking indices on these quantities do now
implicitly stand for different transformation behaviors under Lorentz transformations. One can amend this
possible confusion by a more complicated notation, but this is for practical purposes usually unnecessary, as
long as one keeps in mind that the index itself does not tell the transformation behavior under Lorentz
transformations. In particular, the derivative 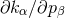 has a mixed transformation behavior and, in a
Taylor-series expansion, this and higher derivatives yield factors that convert the normal to the modified
transformation behavior.
has a mixed transformation behavior and, in a
Taylor-series expansion, this and higher derivatives yield factors that convert the normal to the modified
transformation behavior.
So far this might have seemed like a rewriting, so it is important to stress the following: just writing down the commutation relation leaves the structure under-determined. To completely specify the model, one needs to make an additional assumption about how a Lorentz transformation is defined, how the coordinates in position space ought to be chosen along with those in momentum space under a Lorentz transformation and, most importantly, what the metric on the curved momentum space (and possibly spacetime) is.
Needless to say, the way we have fixed the transformation behavior in this simple example is not the
only way to do it. Another widely used choice is to require that 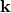 obeys the usual transformation
behavior, yet interpret
obeys the usual transformation
behavior, yet interpret 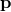 as the physical momentum, or
as the physical momentum, or 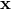 as ‘pseudo-coordinates’ (though this is not a
word that has been used in the literature). We will meet an example of this in Section 4.2.2. This
variety is the main reason why the literature on the subject of modified commutation relations is
confusing.
as ‘pseudo-coordinates’ (though this is not a
word that has been used in the literature). We will meet an example of this in Section 4.2.2. This
variety is the main reason why the literature on the subject of modified commutation relations is
confusing.
At this point it should be mentioned that a function 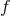 that maps an infinite value of
that maps an infinite value of 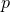 to an
asymptotically-finite value of
to an
asymptotically-finite value of 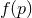 cannot be a polynomial of finite order. Its Taylor series expansion
necessarily needs to have an infinite number of terms. Now if
cannot be a polynomial of finite order. Its Taylor series expansion
necessarily needs to have an infinite number of terms. Now if 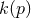 becomes constant for large
becomes constant for large 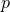 , then
, then
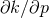 goes to zero and
goes to zero and 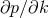 increases without bound, which is why the uncertainty (176*) increases
for large
increases without bound, which is why the uncertainty (176*) increases
for large 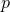 . Depending on the choice of
. Depending on the choice of 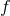 , this might be the case for the spatial or temporal components
or both. If one wants to capture the regularizing properties of the minimal length, then a perturbative
expansion in powers of
, this might be the case for the spatial or temporal components
or both. If one wants to capture the regularizing properties of the minimal length, then a perturbative
expansion in powers of 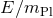 will not work in the high energy limit. In addition, such expansions
generically add the complication that any truncation of the series produces for the dispersion relation a
polynomial of finite order, which will have additional zeros, necessitating additional initial values [158].
This can be prevented by not truncating the series, but this adds other complications, discussed in
Section 4.4.
will not work in the high energy limit. In addition, such expansions
generically add the complication that any truncation of the series produces for the dispersion relation a
polynomial of finite order, which will have additional zeros, necessitating additional initial values [158].
This can be prevented by not truncating the series, but this adds other complications, discussed in
Section 4.4.
Since 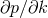 is a function of
is a function of 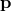 , the position operator
, the position operator 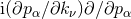 , is not Hermitian if
, is not Hermitian if 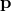 is
Hermitian. This is unfortunate for a quantity that is supposed to be a physical observable, but we have to
keep in mind that the operator itself is not an observable anyway. To obtain an observable, we have to take
an expectation value. To ensure that the expectation value produces meaningful results, we change its
evaluation so that the condition
is
Hermitian. This is unfortunate for a quantity that is supposed to be a physical observable, but we have to
keep in mind that the operator itself is not an observable anyway. To obtain an observable, we have to take
an expectation value. To ensure that the expectation value produces meaningful results, we change its
evaluation so that the condition 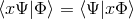 , which in particular guarantees that expectation
values are real, is still fulfilled. That is, we want the operator to be symmetric, rather than
Hermitian.11
To that end, one changes the measure in momentum space to [175, 184*]
, which in particular guarantees that expectation
values are real, is still fulfilled. That is, we want the operator to be symmetric, rather than
Hermitian.11
To that end, one changes the measure in momentum space to [175, 184*]
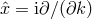 , because now
Note that this does not work without the additional factor because then the integration measure does not
fit to the derivative, which is a consequence of the modified commutation relations. We will see in the next
section that there is another way to think of this modified measure.
, because now
Note that this does not work without the additional factor because then the integration measure does not
fit to the derivative, which is a consequence of the modified commutation relations. We will see in the next
section that there is another way to think of this modified measure.
The mass-shell relation, 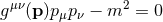 , is invariant under normal Lorentz transformations
acting on
, is invariant under normal Lorentz transformations
acting on 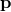 , and thus
, and thus 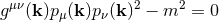 is invariant under the modified Lorentz
transformations acting on
is invariant under the modified Lorentz
transformations acting on 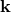 . The clumsy notation here has stressed that the metric on momentum space
will generally be a non-linear function of the coordinates. The mass-shell relation will yield the Hamiltonian
constraint of the theory.
. The clumsy notation here has stressed that the metric on momentum space
will generally be a non-linear function of the coordinates. The mass-shell relation will yield the Hamiltonian
constraint of the theory.
There is a subtlety here; since 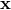 is not Hermitian, we can’t use the representation if this operator. The
way this can be addressed depends on the model. One can in many cases just work the momentum
representation. In our example, we would note that the operator
is not Hermitian, we can’t use the representation if this operator. The
way this can be addressed depends on the model. One can in many cases just work the momentum
representation. In our example, we would note that the operator 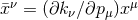 is Hermitian, and use
its representation. In this representation, the Hamiltonian constraint becomes a higher-order operator, and
thus delivers a modification of the dispersion relation. However, the interpretation of the dispersion then
hinges on the interpretation of the coordinates. Depending on the suitable identification of position space
coordinates and the function
is Hermitian, and use
its representation. In this representation, the Hamiltonian constraint becomes a higher-order operator, and
thus delivers a modification of the dispersion relation. However, the interpretation of the dispersion then
hinges on the interpretation of the coordinates. Depending on the suitable identification of position space
coordinates and the function 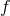 , the speed of massless particles in this model may thus become a function
of the momentum four-vector
, the speed of massless particles in this model may thus become a function
of the momentum four-vector 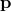 . It should be noted however that this is not the case for all choices of
. It should be noted however that this is not the case for all choices of
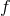 [155*].
[155*].
Many of the applications of this model that we will meet later only use the first or second-order
expansion of 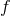 . While these are sufficient for some interesting consequences of the GUP, the Planck
energy is then generically not an asymptotic and invariant value. If the complete function
. While these are sufficient for some interesting consequences of the GUP, the Planck
energy is then generically not an asymptotic and invariant value. If the complete function 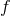 is considered,
it is usually referred to as an ‘all order GUP.’ The expansion to first or second order is often helpful
because it allows one to parameterize the possible modifications by only a few dimensionless
quantities.
is considered,
it is usually referred to as an ‘all order GUP.’ The expansion to first or second order is often helpful
because it allows one to parameterize the possible modifications by only a few dimensionless
quantities.
To restrict the form of modifications possible in this approach, sometimes the Jacobi identities are drawn
upon. It is true that the Jacobi identities restrict the possible commutation relations, but seen as we did
here starting from the standard commutation relations, this statement is somewhat misleading. The Jacobi
identities are, as the name says, identities. They say more about the properties of the binary operation they
represent than about the quantities this operation acts on. They are trivially fulfilled for the commutators
of all new variables 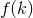 one can define (coordinates one can choose) if the old ones fulfilled the identities.
However, if one does not start from such a function, one can draw upon the Jacobi identities as a
consistency check.
one can define (coordinates one can choose) if the old ones fulfilled the identities.
However, if one does not start from such a function, one can draw upon the Jacobi identities as a
consistency check.
A requirement that does put a restriction on the possible form of the commutation relation is that of
rotational invariance. Assuming that 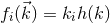 , where
, where 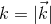 , one has
, one has
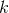 is
We denote the inverse of
is
We denote the inverse of 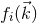 with
with 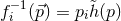 . An expansion of
. An expansion of 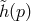 and comparison of
coefficients yields to third order
With this, one has then
For the dimensions to match, the constant
and comparison of
coefficients yields to third order
With this, one has then
For the dimensions to match, the constant 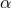 must have a dimension of length and
must have a dimension of length and 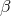 a dimension of
length squared. One would expect this length to be of the order Planck length and play the role of the
fundamental length.
a dimension of
length squared. One would expect this length to be of the order Planck length and play the role of the
fundamental length.
It is often assumed that 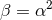 , but it should be noted that this does not follow from the above. In
particular,
, but it should be noted that this does not follow from the above. In
particular, 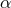 may be zero and the modification be even in
may be zero and the modification be even in 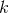 , starting only at second order. Note that
an expansion of the commutator in the form
, starting only at second order. Note that
an expansion of the commutator in the form ![[xi,pj] = iδij(1 + βp2)](article805x.gif) does not fulfill the above
requirement.
does not fulfill the above
requirement.
To summarize this section, we have seen that a GUP that gives rise to a minimal length scale can be realized by modifying the canonical commutation relations. We have seen that this modification alone does not completely specify the physical picture, we have in addition to fix the transformation behavior under Lorentz transformations and the metric on momentum space. In Section 4.2.2 we will see how this can be done.
4.2.2 The Snyder basis
As mentioned in the previous example, 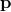 is not canonically conjugate to
is not canonically conjugate to 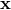 , and the wave vector
, and the wave vector 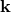 ,
which is canonically conjugate, is the quantity that transforms under the modified Lorentz transformations.
But that is not necessarily the case for models with modified commutation relations, as we will see in this
section.
,
which is canonically conjugate, is the quantity that transforms under the modified Lorentz transformations.
But that is not necessarily the case for models with modified commutation relations, as we will see in this
section.
Let us start again from the normal commutation relations (174*) and now define new position
coordinates 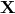 by
by 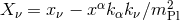 , as discussed in [135]. (The Planck mass
, as discussed in [135]. (The Planck mass 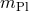 could enter
here with an additional dimensionless factor that one would expect to be of order one, if one describes a
modification that has its origin in quantum gravitational effects. In the following we will not carry around
such an additional factor. It can easily be inserted at any stage just by replacing
could enter
here with an additional dimensionless factor that one would expect to be of order one, if one describes a
modification that has its origin in quantum gravitational effects. In the following we will not carry around
such an additional factor. It can easily be inserted at any stage just by replacing 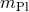 with
with 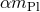 .) In
addition, we now require that
.) In
addition, we now require that 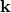 transforms under the normal Lorentz transformations. With this
replacement, the
transforms under the normal Lorentz transformations. With this
replacement, the 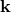 ’s are then still commutative as usual and the remaining commutation relations have
the form
’s are then still commutative as usual and the remaining commutation relations have
the form
The commutator between 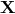 and
and 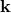 leads to a GUP by taking the expectation value in the same
way as previously, though the reason here is a different one: If it is the
leads to a GUP by taking the expectation value in the same
way as previously, though the reason here is a different one: If it is the 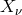 ’s that are representing
physically-meaningful positions in spacetime, then it is their non-commutativity that spoils the resolution of
structures at the Planck scale. Note that the transformation from
’s that are representing
physically-meaningful positions in spacetime, then it is their non-commutativity that spoils the resolution of
structures at the Planck scale. Note that the transformation from 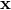 to
to 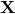 is not canonical exactly for
the reason that it does change the commutation relations.
is not canonical exactly for
the reason that it does change the commutation relations.
In a commonly-used notation, 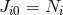 are the generators of boosts and
are the generators of boosts and 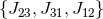 are the
generators of the rotations
are the
generators of the rotations 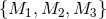 that fulfill the normal Lorentz algebra
that fulfill the normal Lorentz algebra
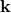 , in the
, in the 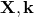 phase-space
coordinates one also has
phase-space
coordinates one also has
There are two notable things here. First, as in Section 4.2.2, the Lorentz algebra remains entirely
unmodified. Second, the 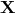 by construction transforms covariantly under normal Lorentz transformations
if the
by construction transforms covariantly under normal Lorentz transformations
if the 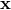 and
and 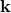 do. However, we see that there is exactly one
do. However, we see that there is exactly one 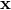 for which
for which 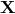 does not depend on
does not depend on
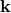 , and that is
, and that is 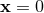 . If we perform a translation by use of the generator
. If we perform a translation by use of the generator 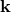 ; the coordinate
; the coordinate 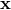 will be
shifted to some value
will be
shifted to some value 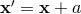 . Alternatively, one may try to take a different generator
for translations than
. Alternatively, one may try to take a different generator
for translations than 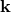 , the obvious choice is the operator canonically conjugated to
, the obvious choice is the operator canonically conjugated to 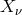
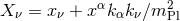 with
with 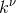 , one can invert
, one can invert 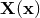 to
Then one finds the translation operator
Therefore, it has been argued [230] that one should understand this type of theory as a modification of
translation invariance rather than a modification of Lorentz symmetry. However, this depends on which
variables are assigned physical meaning, which is a question that is still under discussion.
to
Then one finds the translation operator
Therefore, it has been argued [230] that one should understand this type of theory as a modification of
translation invariance rather than a modification of Lorentz symmetry. However, this depends on which
variables are assigned physical meaning, which is a question that is still under discussion.
We should at this point look at Snyder’s original motivation for it is richer than just the commutation relations of position, momenta and generators and adds to it in an important way. Snyder originally considered a 5-dimensional flat space of momenta, in which he looked at a hypersurface with de Sitter geometry. The full metric has the line element
where the coordinates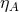 have dimensions of energy and capital Latin indices run from 0 to
4. This flat space is invariant under the action of the group
have dimensions of energy and capital Latin indices run from 0 to
4. This flat space is invariant under the action of the group 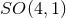 , which has a total of
10 generators. In that 5-dimensional space, consider a 4-dimensional hyperboloid defined by
This hypersurface is invariant under the
, which has a total of
10 generators. In that 5-dimensional space, consider a 4-dimensional hyperboloid defined by
This hypersurface is invariant under the 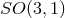 subgroup of
subgroup of 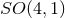 . It describes a
de Sitter space and can be parameterized by four coordinates. Snyder chooses the projective
coordinates
. It describes a
de Sitter space and can be parameterized by four coordinates. Snyder chooses the projective
coordinates 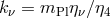 . (These coordinates are nowadays rarely used to parameterize
de Sitter space, as the fifth coordinate of the embedding space
. (These coordinates are nowadays rarely used to parameterize
de Sitter space, as the fifth coordinate of the embedding space 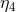 is not constant on the
hyperboloid.) The remaining four generators of
is not constant on the
hyperboloid.) The remaining four generators of 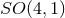 are then identified with the coordinates
From this one obtains the same commutation relations (193*), (195*), and (196*) as above [55].
are then identified with the coordinates
From this one obtains the same commutation relations (193*), (195*), and (196*) as above [55].
However, the Snyder approach contains additional information: We know that the commutation relations
seen previously can be obtained by a variable substitution from the normal ones. In addition, we know that
the momentum space is curved. It has a de Sitter geometry, a non-trivial curvature tensor and curvature
scalar 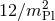 . It has the corresponding parallel transport and a volume measure. In these coordinates,
the line element has the form
. It has the corresponding parallel transport and a volume measure. In these coordinates,
the line element has the form
The 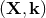 coordinates on phase space have become known as the Snyder basis.
coordinates on phase space have become known as the Snyder basis.
4.2.3 The choice of basis in phase space
The coordinates 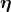 that Snyder chose to parameterize the hyperbolic 4-dimensional submanifold are not
unique. There are infinitely many sets of coordinates we can choose on this space; most of them will be
non-linear combinations of each other. Such non-linear redefinitions of momenta will change the
commutation relations between position and momentum variables. More generally, the question that arises
here is what coordinates on phase space should be chosen, since we have seen in the previous Section 4.2.2
that a change of coordinates in phase space that mixes position and momentum operators creates
non-commutativity. For example, one could use a transformation that mixes
that Snyder chose to parameterize the hyperbolic 4-dimensional submanifold are not
unique. There are infinitely many sets of coordinates we can choose on this space; most of them will be
non-linear combinations of each other. Such non-linear redefinitions of momenta will change the
commutation relations between position and momentum variables. More generally, the question that arises
here is what coordinates on phase space should be chosen, since we have seen in the previous Section 4.2.2
that a change of coordinates in phase space that mixes position and momentum operators creates
non-commutativity. For example, one could use a transformation that mixes 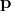 and
and 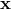 to absorb the
unusual factor in the
to absorb the
unusual factor in the ![[x,p ]](article865x.gif) commutator in (175*) at the expense of creating a non-commutative
momentum space.
commutator in (175*) at the expense of creating a non-commutative
momentum space.
Besides the above-discussed coordinate systems 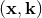 ,
, 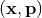 ,
, 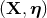 , and
, and 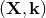 , there are
various other choices of coordinates that can be found in the literature. One choice that is
very common are coordinates
, there are
various other choices of coordinates that can be found in the literature. One choice that is
very common are coordinates 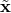 that are related to the Snyder position variables [197*] via
that are related to the Snyder position variables [197*] via
 -Minkowski
spacetime. The name derives from the common nomenclature in which the constant
-Minkowski
spacetime. The name derives from the common nomenclature in which the constant 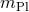 (that, as we have
warned previously, might differ from the actual Planck mass by a factor of order one) is
(that, as we have
warned previously, might differ from the actual Planck mass by a factor of order one) is  .
.
Another choice of coordinates that can be found in the literature [132*, 287*] is obtained by the transformation
on the normal coordinates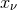 . This leads to the commutation relations
This is the full
. This leads to the commutation relations
This is the full  -Minkowski phase space [205], which is noteworthy because it was shown by
Kowalski-Glikman and Nowak [197*] that the geometric approach to phase space is equivalent to the
algebraic approach that has been pursued by deforming the Poincaré-algebra (the algebra of generators of
Poincaré transformations, i.e., boosts, rotations and momenta) to a Hopf algebra [213*] with deformation
parameter
-Minkowski phase space [205], which is noteworthy because it was shown by
Kowalski-Glikman and Nowak [197*] that the geometric approach to phase space is equivalent to the
algebraic approach that has been pursued by deforming the Poincaré-algebra (the algebra of generators of
Poincaré transformations, i.e., boosts, rotations and momenta) to a Hopf algebra [213*] with deformation
parameter  , the
, the  -Poincaré Hopf algebra, giving rise to the above
-Poincaré Hopf algebra, giving rise to the above  -Minkowski phase space.
-Minkowski phase space.
A Hopf algebra generally consists of two algebras that are related by a dual structure and associated
product rules that have to fulfill certain compatibility conditions. Here, the dual to the  -Poincaré
algebra is the
-Poincaré
algebra is the  -Poincaré group, whose elements are identified as Lorentz transformations and position
variables. The additional structure that we found in the geometric approach to be the curvature of
momentum space is, in the algebraic approach, expressed in the co-products and antipodes of the Hopf
algebra. As in the geometrical approach, there is an ambiguity in the choice of coordinates in phase
space.
-Poincaré group, whose elements are identified as Lorentz transformations and position
variables. The additional structure that we found in the geometric approach to be the curvature of
momentum space is, in the algebraic approach, expressed in the co-products and antipodes of the Hopf
algebra. As in the geometrical approach, there is an ambiguity in the choice of coordinates in phase
space.
In addition to the various choices of position space coordinates, one can also use different coordinates on
momentum space, by choosing different parameterizations of the hypersurface than that of Snyder.
One such parameterization is using coordinates 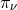 , that are related to the Snyder basis by
, that are related to the Snyder basis by
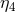 is not constant on the hypersurface.) The
is not constant on the hypersurface.) The 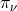 ’s are the bicrossproduct basis of the Hopf
algebra [213], and they make a natural choice for the algebraic approach. With the
’s are the bicrossproduct basis of the Hopf
algebra [213], and they make a natural choice for the algebraic approach. With the  -Minkowski
coordinates
-Minkowski
coordinates 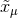 , one then has the commutators [197*]
, one then has the commutators [197*]
Another choice of coordinates on momentum space is the Magueijo–Smolin basis 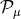 , which is related
to the Snyder coordinates by
, which is related
to the Snyder coordinates by
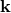 (196*), one can work out the transformation behavior of the
other coordinates, and reexpress the mass-shell condition 204* in the new sets of coordinates.
(196*), one can work out the transformation behavior of the
other coordinates, and reexpress the mass-shell condition 204* in the new sets of coordinates.
Since there are infinitely many other choices of coordinates, listing them all is beyond the scope of this review. So long as one can identify a new set of coordinates by a coordinate transformation from other coordinates, the commutation relations will fulfill the Jacobi identities automatically. Thus, these coordinate systems are consistent choices. One can also, starting from the transformation of the Snyder coordinates, derive the transformation behavior under Lorentz transformation for all other sets of coordinates. For the above examples the transformation behavior can be found in [132*, 197*]
In summary, we have seen here that there are many different choices of coordinates on phase space that lead to modified commutation relations. We have met some oft used examples and seen that the most relevant information is in the geometry of momentum space. Whether there are particular choices of coordinates on phase space that lend themselves to easy interpretations and are thus natural in some sense is presently an open question.
4.2.4 Multi-particle states
One important consequence of the modified Lorentz symmetry that has been left out in our discussion so far is the additivity of momenta, which becomes relevant when considering interactions.
In the example from Section 4.2.1, the function 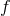 has to be non-linear to allow a maximum
value of (some components of)
has to be non-linear to allow a maximum
value of (some components of) 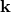 to remain Lorentz invariant, and consequently the Lorentz
transformations
to remain Lorentz invariant, and consequently the Lorentz
transformations 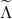 are non-linear functions of
are non-linear functions of 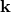 . But that means that the transformation
of a sum of pseudo-momenta
. But that means that the transformation
of a sum of pseudo-momenta 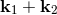 is not the same as the sum of the transformations:
is not the same as the sum of the transformations:
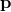 that is the physical momentum that is conserved,
and since it transforms under normal Lorentz transformations its conservation is independent of the rest
frame.
that is the physical momentum that is conserved,
and since it transforms under normal Lorentz transformations its conservation is independent of the rest
frame.
However, if one has chosen the 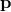 rather than the
rather than the 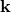 to obey the normal Lorentz transformation, as
was the case in Sections 4.2.2 and 4.2.3, then this equation looks exactly the other way round
to obey the normal Lorentz transformation, as
was the case in Sections 4.2.2 and 4.2.3, then this equation looks exactly the other way round
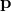 should be conserved in interactions, and the
above sum is supposed to be conserved in an interaction in one rest frame, it would not be conserved
generally in all rest frames. (For the free particle, both
should be conserved in interactions, and the
above sum is supposed to be conserved in an interaction in one rest frame, it would not be conserved
generally in all rest frames. (For the free particle, both 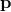 and
and 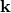 are conserved since the one is a
function of the other.)
are conserved since the one is a
function of the other.)
The solution to this problem is to define a new, non-linear, addition law 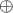 that has the property that
it remains invariant and that can be rightfully interpreted as a conserved quantity. This is straightforward
to do if we once again use the quantities
that has the property that
it remains invariant and that can be rightfully interpreted as a conserved quantity. This is straightforward
to do if we once again use the quantities 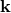 that in this case by assumption transform under the normal
Lorentz transformation. To each momentum we have an associated pseudo-momentum
that in this case by assumption transform under the normal
Lorentz transformation. To each momentum we have an associated pseudo-momentum 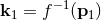 ,
,
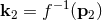 . The sum
. The sum 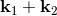 is invariant under normal Lorentz transformations, and so we construct
the sum of the
is invariant under normal Lorentz transformations, and so we construct
the sum of the 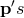 as
as
 -Poincaré algebra [197].
-Poincaré algebra [197].
This new definition for a sum is now observer independent by construction, but we have created a new
problem. If the function 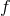 (or some of its components) has a maximum of the Planck mass, then the sum
of momenta will never exceed this maximal energy. The Planck mass is a large energy as far as particle
physics is concerned, but in everyday units it is about
(or some of its components) has a maximum of the Planck mass, then the sum
of momenta will never exceed this maximal energy. The Planck mass is a large energy as far as particle
physics is concerned, but in everyday units it is about 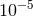 gram, a value that is easily exceeded by some
large molecules. This problem of reproducing a sensible multi-particle limit when one chooses the physical
momentum to transform under modified Lorentz transformations has become known as the ‘soccer-ball
problem.’
gram, a value that is easily exceeded by some
large molecules. This problem of reproducing a sensible multi-particle limit when one chooses the physical
momentum to transform under modified Lorentz transformations has become known as the ‘soccer-ball
problem.’
The soccer-ball problem is sometimes formulated in a somewhat different form. If one makes an
expansion of the function 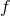 to include the first correction terms in
to include the first correction terms in 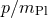 , and from that derives the
sum
, and from that derives the
sum 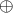 , then it remains to be shown that the correction terms stay small if one calculates sums over a
large number of momenta, whose ordinary sum describes macroscopic objects like, for example, a soccer
ball. One expects that the sum then has approximately the form
, then it remains to be shown that the correction terms stay small if one calculates sums over a
large number of momenta, whose ordinary sum describes macroscopic objects like, for example, a soccer
ball. One expects that the sum then has approximately the form 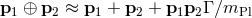 ,
where
,
where 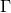 are some coefficients of order one. If one iterates this sum for
are some coefficients of order one. If one iterates this sum for 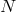 terms, the normal
sum grows with
terms, the normal
sum grows with 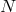 but the additional term with
but the additional term with 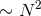 , so that it will eventually become
problematic.
, so that it will eventually become
problematic.
Note that this problem is primarily about sums of momenta, and not even necessarily about bound states. If one does not symmetrize the new addition rule, the result may also depend on the order in which momenta are added. This means in particular the sum of two momenta can depend on a third term that may describe a completely unrelated (and arbitrarily far away) part of the universe, which has been dubbed the ‘spectator problem’ [195, 134].
There have been various attempts to address the problem, but so far none has been generally accepted.
For example, it has been suggested that with the addition of 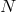 particles, the Planck scale that appears
in the Lorentz transformation, as well as in the modified addition law, should be rescaled to
particles, the Planck scale that appears
in the Lorentz transformation, as well as in the modified addition law, should be rescaled to
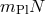 [212, 171*, 210]. It is presently difficult to see how this ad-hoc solution would follow from the
theory. Alternatively, it has been suggested that the scaling of modifications should go with the
density [157*, 246] rather than with the total momentum or energy respectively. While the energy of
macroscopic objects is larger than that of microscopic ones, the energy density decreases instead. This
seems a natural solution to the issue but would necessitate a completely different ansatz to implement. A
noteworthy recent result is [24, 166], where it has been shown how the problem can be alleviated in
a certain model, such that the nonlinear term in the sum does not go with
[212, 171*, 210]. It is presently difficult to see how this ad-hoc solution would follow from the
theory. Alternatively, it has been suggested that the scaling of modifications should go with the
density [157*, 246] rather than with the total momentum or energy respectively. While the energy of
macroscopic objects is larger than that of microscopic ones, the energy density decreases instead. This
seems a natural solution to the issue but would necessitate a completely different ansatz to implement. A
noteworthy recent result is [24, 166], where it has been shown how the problem can be alleviated in
a certain model, such that the nonlinear term in the sum does not go with 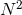 but with
but with
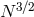 .
.
One should also note that this problem does not occur in the case in which the modification is present only off-shell, which seems to be suggested in some interpretations. Then, if one identifies the momenta of particles as those of the asymptotically free states, the addition of their momenta is linear as usual. For the same reason, the problem also does not appear in the interpretation of such modifications of conservation laws as being caused by a running Planck’s constant, put forward [261, 74*], and discussed in Section 3.5. In this case, the relevant energy is the momentum transfer, and for bound states this remains small if the total mass increases.
So we have seen that demanding the physical momentum rather than the pseudo-momentum to transform under modified Lorentz transformations leads to the soccer ball and the spectator problem. This is a disadvantage of this choice. On the other hand, this choice has the advantage that it has a geometric base, which is missing for the case discussed in Section 4.2.1.
4.2.5 Open problems
We have, in Section 4.2.2 and 4.2.3, seen different examples for modified commutation relations with a curved momentum space. But commutation relations alone don’t make for physics. To derive physical meaning, one has to define the dynamics of the system and its observables.
This raises the question of which principles to use for the dynamics and how to construct observables. While there are several approaches to this, some of which we will meet in the following, there exists to date no agreed-upon framework by which to derive observables, and therefore the question of whether there is a physical reason to prefer one basis over another is open.
One finds some statements in the literature that a different choice of coordinates leads to a different physics, but this statement is somewhat misleading. One should more precisely say that a choice of coordinates and the corresponding commutation relations do not in and of themselves determine the physics. For that, one has to specify not only the geometry of the phase space, which is not contained merely in the commutation relations, but also a unique procedure to arrive at equations of motion.
Given the complete geometry (or, equivalently, the operations on the Hopf algebra), the
Hamiltonian in some basis can be identified as (a function of) the Casimir operator of the Lorentz
group.12
It can be expressed in any basis one wishes by substitution. However, if the transformation between one
basis of phase space and the other is not canonical, then transforming the Hamiltonian by substitution will
not preserve the Hamiltonian equations. In particular, 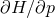 and
and ![[H, x ]](article931x.gif) will generically not yield the
same result, thus the notion of velocity requires careful interpretation, especially when the coordinates in
position space are in addition non-commuting. It has been argued by Smolin in [286*] that commuting
coordinates are the sensible choice. The construction of observables with non-commuting coordinates has
been worked towards, e.g., in [287*, 286*, 169*, 27*, 23*, 21*, 272, 302, 136].
will generically not yield the
same result, thus the notion of velocity requires careful interpretation, especially when the coordinates in
position space are in addition non-commuting. It has been argued by Smolin in [286*] that commuting
coordinates are the sensible choice. The construction of observables with non-commuting coordinates has
been worked towards, e.g., in [287*, 286*, 169*, 27*, 23*, 21*, 272, 302, 136].
The one modification that all of these approaches have in common is a non-trivial measure in momentum space that in the geometric approach results from the volume element of the now curved space. But this raises the question of what determines the geometry. Ideally one would like an axiomatic approach that allows one to derive the geometry from an underlying principle, and then everything else from the geometry. One would, in the general case, if dynamical matter distributions are present, not expect the structure of momentum space to be entirely fixed. A step towards a dynamical momentum space has been made in [86], but clearly the topic requires more investigation.
Another open problem with this class of models is the type of non-locality that arises. If the Planck length acts as a minimal length, there clearly has to be some non-locality. However, it has been shown that for those types of models in which the speed of light becomes energy dependent, the non-locality becomes macroscopically large. Serious conceptual problems arising from this were pointed out in [16, 277, 156], and shown to be incompatible with observation in [159, 160].
A very recent development to address this problem is to abandon an absolute notion of locality, and instead settle for a relative one. This ‘principle of relative locality’ [287*, 286*, 169*, 27*, 23*, 21*, 79*] is a promising development. It remains to be seen how it mitigates the problem of non-local particle interactions. For some discussion, see [162, 163, 161]. It should be stressed that this problem does not occur if the speed of light remains constant for free particles.
4.3 Quantum mechanics with a minimal length scale
So we have seen that modified commutation relations necessarily go together with a GUP, a modified measure in momentum space and a modified Lorentz symmetry. These models may or may not give rise to a modified on-shell dispersion relation and thus an energy-dependent speed of light [155], but the modified commutation relations and the generalized uncertainty cannot be treated consistently without taking care of the momentum space integration and the transformation behavior.
The literature on the subject of quantum mechanics with a minimal length scale is partly confusing because many models use only some of the previously-discussed ingredients and do not subscribe to all of the modifications, or at least they are not explicitly stated. Some differ in the interpretation of the quantities; notoriously there is the question of what is a physically-meaningful definition of velocity and what is the observable momentum.
Thus, the topic of a minimal length scale has thus given rise to many related approaches that run under the names ‘modified commutation relation,’ ‘generalized uncertainty,’ ‘deformed special relativity,’ ‘minimal length deformed quantum mechanics,’ etc. and are based on only some features of the modified phase space discussed previously. It is not clear in all cases whether this is consistently possible or what justifies a particular interpretation. For example, one may argue that in the non-relativistic limit, a modified transformation behavior under boosts, that would only become relevant at relativistic energies, is irrelevant. However, one has to keep in mind that the non-linear transformation behavior of momenta results in a non-linear addition law, which becomes problematic for the treatment of multi-particle states. Thus, even in the non-relativistic case, one has to be careful if one deals with a large number of particles.
The lack of clean, agreed upon, axiomatic approach has inevitably given rise to occasional criticism. It has been argued in [5], for example, that the deformations of special relativity are operationally indistinguishable from special relativity. Such misunderstandings are bound to arise if the model is underspecified. Maybe, the easiest way to see that the minimal length modified quantum theory is not equivalent to the unmodified case is to keep in mind that the momentum space is curved: There is no coordinate transformation that will make the curvature of momentum space go away. The non-trivial metric will also produce an infinite series of higher-order derivatives in the Hamiltonian constraint, a reflection of the non-locality that the existence of a minimal length scale implies.
In the following, we will not advocate one particular approach, but just report what results are presently available. Depending on which quantities are raised to physical importance, the resulting model can have very different properties. The speed of light might be energy dependent [26*] or not [301*, 99*], there might be an upper limit to energies and/or momenta, or not, addition laws and thresholds might be modified, or not, coordinates might be non-commuting, or not, there might be non-localities or not, the modification might only be present off-shell, or not. This is why the physical meaning of different bases in phase space is a problem in need of being addressed in order to arrive at more stringent predictions.
4.3.1 Maximal localization states
The most basic information about the minimal length modified quantum mechanics is in the position operator itself. While, in the momentum representation, there exist eigenvectors of the position operator that correspond to arbitrarily–sharply-peaked wave functions, these do not describe physically-possible configurations. It has been shown in [184*] that the sharply-peaked wavefunctions with spread below the minimal position uncertainty carry an infinite energy, and thus do not represent a physically-meaningful basis. Instead, one can construct quasi-localized states that are as sharply focused as physically possible. These states are then no longer exactly orthogonal. In [184*], the maximal localization states have been constructed in one spatial dimension for a 2nd-order expansion of the GUP.
4.3.2 The Schrödinger equation with potential
The most straight-forward modification of quantum mechanics that one can construct with the modified commutation relations is leaving the Hamiltonian unmodified. For the harmonic oscillator for example, one then has the familiar expression
However, due to the modified commutation relations, if one inserts the operators, the resulting differential equation becomes higher order. In one dimension, for example, in the momentum space representation, one would have to second order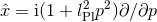 and thus for the stationary equation
and thus for the stationary equation
The same procedure can be applied to other types of potentials in the Schrödinger equation, and in principle this can be done not only in the small-momentum expansion, but to all orders. In this fashion, in the leading-order approximation, the harmonic oscillator in one dimension has been studied in [184, 167*, 8*, 125], the harmonic oscillator in arbitrary dimensions in [83*, 177, 85, 93], the energy levels of the hydrogen atom in [167*, 69, 296, 67, 258], the particle in a box in [7], Landau levels and the tunneling current in [8*, 96, 97*], the uniform gravitational potential in [244, 83], the inverse square potential in [65, 66], neutrino oscillations in [292], reflection and transmission coefficients of a potential step and potential barrier in [8, 97], the Klein paradox in [124], and corrections to the gyromagnetic moment of the muon in [143, 95]. Note that these leading order expansions do not all use the same form of the GUP.
In order to obtain the effects of the minimal length on the transition rate of ultra cold neutrons in gravitational spectrometers, Pedram et al. calculated the quantization of the energy spectrum of a particle in a linear gravitational field in the GUP leading-order approximation [259] and to all orders [256]. The harmonic oscillator in one dimension with an asymptotic GUP has been considered in [257*, 255].
While not, strictly speaking, falling into the realm of quantum mechanics, let us also mention here the Casimir effect, which has been studied in [142, 46, 241, 112, 102], and Casimir–Polder intermolecular forces, which have been looked at in [252].
All these calculations do, in principle, cause corrections to results obtained in standard quantum mechanics. As one expects, the correction terms are unobservably small if one assumes the minimal length scale to be on the order of the Planck length. However, as argued previously, since we have no good explanation as to why the Planck length as the scale at which quantum gravity should become important is so small, the minimal length should, in principle, be regarded as a free parameter and then be bound by experiment. A compilation of bounds from the above calculations is presently not available and unfortunately no useful comparison is possible due to the different parameterizations and assumptions used. One can hope that this might improve in the future if a more standardized approach becomes established, for example, using the parameterization (192*).
4.3.3 The Klein–Gordon and Dirac equation
The Klein Gordon equation can be obtained directly from the invariant 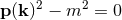 . The Dirac
equation can be constructed using the same prescription that lead to the Schrödinger equation, except
that, to make sure Lorentz invariance is preserved, one should first bring it into a suitable form
. The Dirac
equation can be constructed using the same prescription that lead to the Schrödinger equation, except
that, to make sure Lorentz invariance is preserved, one should first bring it into a suitable form
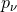 with its operator as discussed in Section 4.2.1. In the position representation, this
will generally produce higher-order derivatives not only in the spatial, but also in the temporal,
components. In order to obtain the Hamiltonian that generates the time evolution, one then has to invert
the temporal part.
with its operator as discussed in Section 4.2.1. In the position representation, this
will generally produce higher-order derivatives not only in the spatial, but also in the temporal,
components. In order to obtain the Hamiltonian that generates the time evolution, one then has to invert
the temporal part.
The Dirac equation with modified commutation relations has been discussed in [167*, 188*]. The Klein–Gordon equation and the Dirac particle in a rectangular and spherical box has been examined in [98].
4.4 Quantum field theory with a minimal length scale
One can construct a quantum field theory along the lines of the quantum mechanical treatment, starting with the modified commutation relations. If the position-space coordinates are non-commuting with a constant Poisson tensor, this leads to the territory of non-commutative quantum field theory for which the reader is referred to the literature specialized on that topic, for example [104, 151] and the many references therein.
Quantum field theory with the  -Poincaré algebra on the non-commuting
-Poincaré algebra on the non-commuting  -Minkowski
spacetime coordinates has been pioneered in [174, 178, 183]. In [176] it has been shown that
introducing the minimal length uncertainty principle into quantum field theory works as a
regulator in the ultraviolet, at least for
-Minkowski
spacetime coordinates has been pioneered in [174, 178, 183]. In [176] it has been shown that
introducing the minimal length uncertainty principle into quantum field theory works as a
regulator in the ultraviolet, at least for 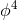 theory. Recently, there has been a lot of progress
on the way towards field quantization [31], by developing the Moyal–Weyl product, the Fock
space [75, 34], and the conserved Noether charges [113, 4, 35]. The case of scalar field theory has been
investigated in [33, 226]. A different second-order modification of the commutation relation has been
investigated for the spinor and Klein–Gordon field in [233] and [232] respectively. [77] studied the
situation in which the Hamiltonian remains unmodified and only the equal time commutation
relations are modified. There are, as yet, not many applications in the literature that investigate
modifications of the standard model of particle physics, but one can expect these to follow
soon.
theory. Recently, there has been a lot of progress
on the way towards field quantization [31], by developing the Moyal–Weyl product, the Fock
space [75, 34], and the conserved Noether charges [113, 4, 35]. The case of scalar field theory has been
investigated in [33, 226]. A different second-order modification of the commutation relation has been
investigated for the spinor and Klein–Gordon field in [233] and [232] respectively. [77] studied the
situation in which the Hamiltonian remains unmodified and only the equal time commutation
relations are modified. There are, as yet, not many applications in the literature that investigate
modifications of the standard model of particle physics, but one can expect these to follow
soon.
Parallel to this has been the development of quantum field theory in the case where coordinates are commuting, the physical momentum transforms under the normal Lorentz transformation, and the speed of light is constant [167*]. This approach has the advantage of being easier to interpret, yet has the disadvantage of delivering more conservative predictions. In this approach, the modifications one is left with are the modified measure in momentum space and the higher-order derivatives that one obtains from the metric in momentum space. The main difficulty in this approach is that, when one takes into account gauge invariance, one does not only obtain an infinite series of higher-derivate corrections to the propagator, one also obtains an infinite number of interaction terms. Whether these models are unitary is an open question.
In order to preserve the super-Planckian limit that is necessary to capture the presence of the
UV-regulating properties, it has been suggested in [167*] that one expand the Lagrangian in
terms of 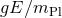 , where
, where 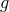 is the coupling constant and
is the coupling constant and 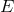 is the energy scale. This means
that the corrections to the propagator (which do not contain any
is the energy scale. This means
that the corrections to the propagator (which do not contain any 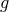 ) are kept entirely, but
one has only the first vertex of the infinite series of interaction terms. One can then explore
the interesting energy range
) are kept entirely, but
one has only the first vertex of the infinite series of interaction terms. One can then explore
the interesting energy range 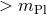 until
until 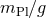 . The virtue of this expansion, despite its
limited range of applicability, is that, by not truncating the power series of the propagator,
one does not introduce additional poles. The expansion in terms of
. The virtue of this expansion, despite its
limited range of applicability, is that, by not truncating the power series of the propagator,
one does not introduce additional poles. The expansion in terms of 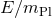 was looked at
in [188].
was looked at
in [188].
In this modified quantum field theory, in [152] the running gauge couplings, possibly with additional compactified spatial dimensions, were investigated. In [189], the electro-weak gauge interaction with minimal length was studied. In [231], the top quark phenomenology in the case with a lowered Planck scale was studied, and in [153, 81] it has been argued that if the Planck scale is indeed lowered, then its role as a minimal length would decrease the production of black holes.
One recurring theme in these models is the suppression of phase space at high energies [167], which is a
direct consequence of the modified measure in momentum space. This has also been found, for the same
reason, in the  -Poincaré approach [311]. Another noteworthy feature of these quantum field theories
with a minimal length is that the commutator between the fields
-Poincaré approach [311]. Another noteworthy feature of these quantum field theories
with a minimal length is that the commutator between the fields 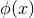 and their canonical conjugate
and their canonical conjugate
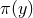 are not equal to a delta function [157, 221], which is an expression of the non-locality that the
higher-order derivatives bring in.
are not equal to a delta function [157, 221], which is an expression of the non-locality that the
higher-order derivatives bring in.
In [190] it has furthermore been suggested that one apply this modification of the quantization procedure to quantum cosmology, which is a promising idea that might allow one to make contact with phenomenology.
4.5 Deformed Special Relativity
Deformed special relativity (DSR) is concerned with the departure from Lorentz symmetry that results from the postulate that the Planck energy transforms like a (component of a) momentum four vector and remains an invariant, maximal energy scale. While the modified commutation relations necessarily give rise to some version of DSR, one can also try to extract information from the deformation of the Lorentz symmetry, or the addition law, directly. This gives rise to what Amelino-Camelia has dubbed ‘test theories’ [18]: simplified and reduced versions of the quantum theory with a minimal length. Working with these test theories has the advantage that one can make contact with phenomenology without working out the – still not very well understood – second quantization and interaction. It has the disadvantage that it makes the ambiguity in identifying physically-meaningful observables worse.
The literature on the topic is vast, and we can not cover it in totality here. For more details on the DSR phenomenology, the reader is referred to [19*, 20*]. We will just mention the most relevant properties of these types of models here.
As we have seen earlier, a non-linear relation 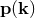 , where
, where 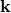 transforms under a normal Lorentz
transformation, generates the deformed Lorentz transformation for
transforms under a normal Lorentz
transformation, generates the deformed Lorentz transformation for 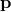 by Eq. (181*). Note that in DSR it
is the non-linearly transforming
by Eq. (181*). Note that in DSR it
is the non-linearly transforming 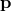 that is considered the physical momentum, while the
that is considered the physical momentum, while the 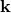 that
transforms under the normal Lorentz transformation is considered the pseudo-momentum. There is an
infinite number of such functions, and thus there is an infinite number of ways to deform special
relativity.
that
transforms under the normal Lorentz transformation is considered the pseudo-momentum. There is an
infinite number of such functions, and thus there is an infinite number of ways to deform special
relativity.
We have already met the common choices in the literature; they constitute bases in  -Minkowski
phase space, for example, the coordinates (211*) proposed by Magueijo and Smolin in [211]. With this
relation, a boost in the
-Minkowski
phase space, for example, the coordinates (211*) proposed by Magueijo and Smolin in [211]. With this
relation, a boost in the  -direction takes the form
-direction takes the form
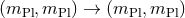 , and thus keeps the Planck energy invariant. Note that since
, and thus keeps the Planck energy invariant. Note that since
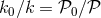 , a so defined speed of light remains constant in this case.
, a so defined speed of light remains constant in this case.
Another example that has entered the literature under the name DSR1 [71] makes use of the bicrossproduct basis (209*). Then, the dispersion relation for massless particles takes the form
The relation between the momenta and the pseudo-momenta and their inverse has been worked out in [171]. In this example, the speed of massless particles that one derives from the dispersion relation depends on the energy of the particle. This effect may be observable in high-frequency light reaching Earth from distant sources, for example from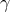 -ray bursts. This interesting prediction is covered in more detail
in [26*, 19*, 20*].
-ray bursts. This interesting prediction is covered in more detail
in [26*, 19*, 20*].
As discussed in Section 4.2.4, the addition law in this type of model has to be modified in order to obtain Lorentz-invariant conserved sums of momenta. This gives rise to the soccer-ball problem and can lead to changes in thresholds of particle interactions [19*, 20*, 78]. It had originally been argued that this would shift the GZK cut-off [17], but this argument has meanwhile been revised. However, in the ‘test theory’ one does not actually have a description of the particle interaction, so whether or not the kinematical considerations would be realized is unclear.
In these two DSR theories, it is usually assumed that the position variables conjugated to 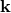 are not
commutative [99*], thereby delivering a particular realization of
are not
commutative [99*], thereby delivering a particular realization of  -Minkowski space. In the DSR1 model,
the speed of massless particles that one derives from the above dispersion relation (220*) is energy
dependent. However, the interpretation of that speed hinges on the meaning of the conjugated
position-space coordinates, which is why it has also been argued that the physically-meaningful speed is
actually constant [301, 99]. Without an identification of observable positions, it is then also difficult to say
whether this type of model actually realizes a minimal length. One can expect that recent work on the
principle of relative locality [287, 286, 169, 27, 23, 21, 79] will shed light on this question. A
forthcoming review [196] will be especially dedicated to the development of relative locality.
-Minkowski space. In the DSR1 model,
the speed of massless particles that one derives from the above dispersion relation (220*) is energy
dependent. However, the interpretation of that speed hinges on the meaning of the conjugated
position-space coordinates, which is why it has also been argued that the physically-meaningful speed is
actually constant [301, 99]. Without an identification of observable positions, it is then also difficult to say
whether this type of model actually realizes a minimal length. One can expect that recent work on the
principle of relative locality [287, 286, 169, 27, 23, 21, 79] will shed light on this question. A
forthcoming review [196] will be especially dedicated to the development of relative locality.
4.6 Composite systems and statistical mechanics
As mentioned previously, a satisfactory treatment of multi-particle states in those models in which the free particles’ momenta are bound by a maximal energy scale is still lacking. Nevertheless, approaches to the description of composite systems or many particle states have been made, based on the modified commutation relations either without subscribing to the deformed Lorentz transformations, and thereby generically breaking Lorentz invariance, or by employing an ad hoc solution by rescaling the bound on the energy with the number of constituents. While these approaches are promising in so far that modified statistical mechanics at Planckian energies would allow one to use the early universe as a laboratory, they should be regarded with some caution, because the connection to the single particle description with deformed Lorentz symmetry is missing, and the case in which Lorentz symmetry is broken is strongly constrained already [191].
That having been said, the statistical mechanics from the  -Poincaré algebra was investigated in
general in [194, 109]. In [268] corrections to the effective Hamiltonian of macroscopic bodies have been
studied, and in [264*] observational consequences of modified commutation relations for a massive oscillator
have been considered. In [172] statistical mechanics with a generalized uncertainty and possible
applications for cosmology have been looked at. The partition functions of minimal-length quantized
statistical mechanics have been derived in [257], in [6] the consequences of the GUP on the
Liouville theorem were investigated, and in [84] the modification of the density of states and the
arising consequences for black-hole thermodynamics were studied. In [242], one finds the effects
of the GUP on the thermodynamics of ultra-relativistic particles in the early universe, and
relativistic thermodynamics in [94]. [312] studied the equation of state for ultra-relativistic Fermi
gases in compact stars, the ideal gas was addressed in [82] and photon gas thermodynamics
in [320].
-Poincaré algebra was investigated in
general in [194, 109]. In [268] corrections to the effective Hamiltonian of macroscopic bodies have been
studied, and in [264*] observational consequences of modified commutation relations for a massive oscillator
have been considered. In [172] statistical mechanics with a generalized uncertainty and possible
applications for cosmology have been looked at. The partition functions of minimal-length quantized
statistical mechanics have been derived in [257], in [6] the consequences of the GUP on the
Liouville theorem were investigated, and in [84] the modification of the density of states and the
arising consequences for black-hole thermodynamics were studied. In [242], one finds the effects
of the GUP on the thermodynamics of ultra-relativistic particles in the early universe, and
relativistic thermodynamics in [94]. [312] studied the equation of state for ultra-relativistic Fermi
gases in compact stars, the ideal gas was addressed in [82] and photon gas thermodynamics
in [320].
4.7 Path-integral duality
In Sections 3.2.4 and 3.4 we have discussed two motivations for limits of spacetime distances that manifest themselves in the Green’s function. While one may question how convincing these motivations are, the idea is interesting and may be considered as a model on its own right. Such a modification that realizes a finite ‘zero point length’ of spacetime intervals had been suggested by Padmanabhan [247, 249, 250, 251*] as a way to effectively take into account metric fluctuations below the Planck scale (the motivation from string theory discussed in Section 3.2.4 was added after the original proposal). This model has the merit of not requiring a modification of Lorentz invariance.
The starting point is to rewrite the Feynman propagator 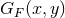 as a sum over all paths
as a sum over all paths 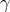 connecting
connecting 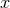 and
and 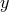
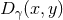 is the proper length of
is the proper length of 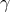 , and
, and 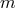 is a constant of dimension mass. Note that the
length of the path depends on the background metric, which is why one expects it to be subject to quantum
gravitational fluctuations. The path integral kernel is
where a dot indicates a derivative with respect to
is a constant of dimension mass. Note that the
length of the path depends on the background metric, which is why one expects it to be subject to quantum
gravitational fluctuations. The path integral kernel is
where a dot indicates a derivative with respect to 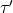 . The relevant difference between the middle and right
expressions in (221*) is that
. The relevant difference between the middle and right
expressions in (221*) is that 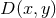 has a square root in it. The equivalence has been shown using a
Euclidean lattice approach in [251*]. Once the propagator is brought into that form, one can apply
Padmanabhan’s postulated “principle of duality” according to which the weight for each path should be
invariant under the transformation
has a square root in it. The equivalence has been shown using a
Euclidean lattice approach in [251*]. Once the propagator is brought into that form, one can apply
Padmanabhan’s postulated “principle of duality” according to which the weight for each path should be
invariant under the transformation 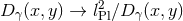 . This changes the propagator (221*) to
Interestingly enough, it can be shown [251] that with this modification in the Schwinger representation,
the path integral kernel remains unmodified, and one merely obtains a change of the weight
When one makes the Fourier transformation of this expression, the propagator in momentum space takes
the form
where
. This changes the propagator (221*) to
Interestingly enough, it can be shown [251] that with this modification in the Schwinger representation,
the path integral kernel remains unmodified, and one merely obtains a change of the weight
When one makes the Fourier transformation of this expression, the propagator in momentum space takes
the form
where 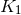 is the modified Bessel function of the first kind. This expression has the limiting values
(compare to Eq. (109*))
is the modified Bessel function of the first kind. This expression has the limiting values
(compare to Eq. (109*))
This postulated duality of the path integral thus suppresses the super-Planckian contributions to
amplitudes. As mentioned in Section 3.2.4, in position space, the Feynman propagator differs from the
ordinary one by the shift 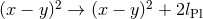 . (This idea is so different not from that of
March [219], who in 1936 proposed to replace ordinary spacetime distances with a modified distance
. (This idea is so different not from that of
March [219], who in 1936 proposed to replace ordinary spacetime distances with a modified distance
 . Though at that time, the ‘minimal length’
. Though at that time, the ‘minimal length’ 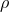 was supposed to be of about the size of the
atomic nucleus. March’s interpretation was that when the newly defined distance between two points
vanishes, the points become indistinguishable.)
was supposed to be of about the size of the
atomic nucleus. March’s interpretation was that when the newly defined distance between two points
vanishes, the points become indistinguishable.)
Some applications for this model for QED, for example the Casimir effect, have been worked out in [294, 282], and consequences for inflation and cosmological models have been looked at in [295, 192]. For a recent criticism see [76].
4.8 Direct applications of the uncertainty principle
Maybe the most direct way to look for effects of the minimal length is to start from the GUP itself. This procedure is limited in its applicability because there are only so many insights one can gain from an inequality for variances of operators. However, cases that can be studied this way are everything that can be concluded from modifications of the Bekenstein argument, and with it corrections to the black-hole entropy that one obtains taking into account the modification of the uncertainty principle and modified dispersion relations.
Most interestingly, in [225, 28] it has been argued that comparing the corrections to the black-hole entropy obtained from the GUP to the corrections obtained in string theory and LQG may be used to restrict the functional form of the GUP.
It has also been argued that taking into account the GUP may give rise to black-hole remnants [2], a
possibility that has been explored in many follow-up works, e.g., [87, 243, 315*]. Corrections to the
thermodynamical properties of a Schwarzschild black hole have been looked at in [22, 321, 100, 214, 217],
the Reissner–Nordström black hole has been considered in [319], and black holes in anti-de Sitter space
in [280, 281, 61]. Black-hole thermodynamics with a GUP has been studied in [201, 237, 54, 186], the
thermodynamics of Kerr–Newman black holes in [315], and the entropy of a charged black hole in 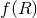 gravity in [273]. In [80] the consequences of the GUP for self-dual black holes found in the mini-superspace
approximation of LQC have been analyzed.
gravity in [273]. In [80] the consequences of the GUP for self-dual black holes found in the mini-superspace
approximation of LQC have been analyzed.
The thermodynamics of anti-de Sitter space has been looked at in [309], and the dynamics of the Taub cosmological model with GUP in [53]. The thermodynamics of Friedmann–Robertson–Walker in four-dimensional spacetimes with GUP can be found in [52, 216], and with additional dimensions in [279]. The relations of the GUP to holography in extra dimensions have been considered in [276], the effects of GUP on perfect fluids in cosmology in [215], and the entropy of the bulk scalar field in the Randall–Sundrum model with GUP in [185]. In [119] it has been suggested that there is a relationship between black-hole entropy and the cosmological constant. The relations of the GUP to Verlinde’s entropic gravity have been discussed in [245]
4.9 Miscellaneous
While most of the work on modified uncertainty relations has focused on the GUP, the consequences of the
spacetime uncertainty that arises in string theory for the spectrum of cosmological perturbations have been
studied in [68*]. In [269] it has been proposed that it might be possible to test Planck scale
modifications of the energy-time uncertainty relation by monitoring tritium decay. It should also be
mentioned that the classical mechanics of  -Poincaré has been worked out in [206], and the
kinematics of a classical free relativistic particle with deformed phase space in [132, 123, 32].
The effects of such a deformed phase space on scalar field cosmology have been investigated
in [263].
-Poincaré has been worked out in [206], and the
kinematics of a classical free relativistic particle with deformed phase space in [132, 123, 32].
The effects of such a deformed phase space on scalar field cosmology have been investigated
in [263].
In [179*] an interesting consequence of the minimal length was studied, the implication of a finite bandwidth for physical fields. Making this connection allows one to then use theorems from classical information theory, such as Shannon’s sampling theorem. It was shown in [179] that fields on a space with minimum length uncertainty can be reconstructed everywhere if known only on a discrete set of points (any set of points), if these points are, on average, spaced densely enough. These continuous fields then have a literally finite information density. In [181], it was shown that this information-theoretic meaning of the minimal length generalizes naturally to curved spacetime and in [182] it was then argued that for this reason spacetime would be simultaneously continuous and discrete in the same way that information can be.
A model for spacetime foam in terms of non-local interactions as a description for quantum gravitational effects, which serves as an origin of a minimal length scale, has been put forward in [121, 122]. This model is interesting because it ties together three avenues towards a phenomenology of quantum gravity: the minimal length scale, decoherence from spacetime foam, and non-locality.
Finally, we mention that a minimum time and length uncertainty in rainbow gravity has been found in [115, 116, 117].

![[xν,xκ] = 0, [xν,kκ] = iδκν , [kν,kκ] = 0. (174 )](article694x.gif)
![[xν,xκ] = 0, [xν,p ] = i∂fκ-, [p ,p ] = 0. (175 ) κ ∂kν ν κ](article702x.gif)

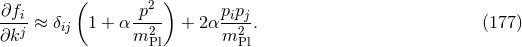
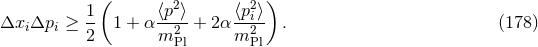
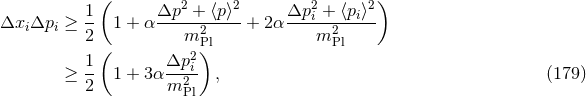

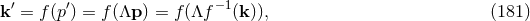
![[J ,p ] = i(p η − p η ). (182 ) κν μ ν κμ κ νμ](article741x.gif)
![[J ,k ] = i(p η − p η ) ∂k-μ, (183 ) κν μ ν κα κ να ∂p α](article743x.gif)
![i k ′ν = kν − --ωαβ[Jαβ,kν] + 𝒪 (ω2 ), (184 ) 2](article744x.gif)
![∂ ( ∂kα ∂kα) [Jκν,xμ] = ixα---- pκηβν ----− pνηβκ ---- (185 ) ∂k μ ∂pβ ∂pκ](article753x.gif)


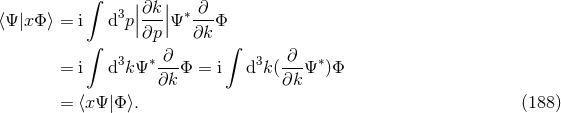

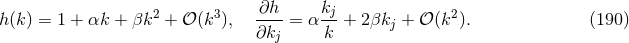

![( ) ( ) [xi,pj] = δij + α k δij + kikj + β k2δij + 2kjki + 𝒪 (k3) k ( pipj) = δij + α pδij + ---- + (β − α2 )p2δij + (2 β − α2)pipj + 𝒪 (p3). (192 ) p](article799x.gif)
![( ) 1 k μkν [Xμ,X ν] = − ----Jμν, [X μ,kν] = i ημν − ---2- , (193 ) mPl m Pl](article816x.gif)
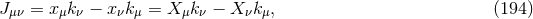
![[N ,N ] = − i𝜖 N , [M ,M ] = i𝜖 N , i j ijk k i j ijk k [Mi,Nj ] = i𝜖ijkNk. (195 )](article826x.gif)
![[Mi, kj] = i𝜖ijkkk, [Mi, k0] = 0, [Ni,kj] = iδijk0, [Ni,k0] = iki. (196 )](article829x.gif)




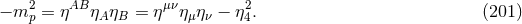
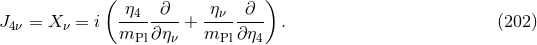



![-xi- [&tidle;x0, &tidle;xi] = − imPl , [&tidle;xi, &tidle;xj] = 0. (206 )](article872x.gif)

![-χi- [χ0,χi] = im , [χi,χj ] = 0, [ki,χj] = iδij, Pl [χ0,k0] = i, [χ0, ki] = − i-ki-, [k0, χi] = i. (208 ) mPl](article878x.gif)
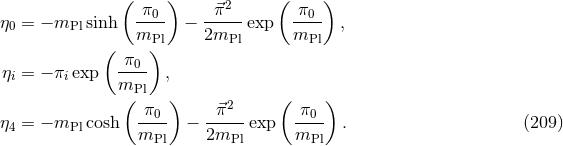
![-πi- [π0, &tidle;x0] = i, [πi, &tidle;x0] = − im , Pl [πi,x&tidle;j] = − iδij, [π0, &tidle;xi] = 0. (210 )](article891x.gif)



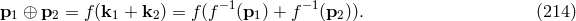

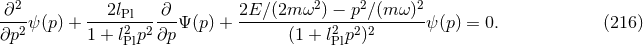

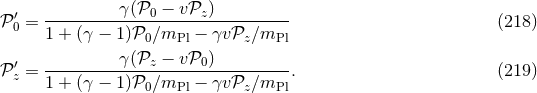

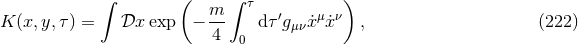
![∑ [ ( l2 )] ^GF (x, y) = exp − m D γ(x,y) + ----Pl--- . (223 ) γ D γ(x,y )](article978x.gif)
![[ ( )] ∫ l2Pl G^F (x,y ) = dτ exp − m τ + --- K (x,y,τ). (224 ) τ](article979x.gif)