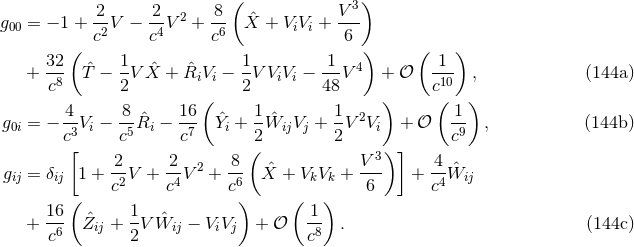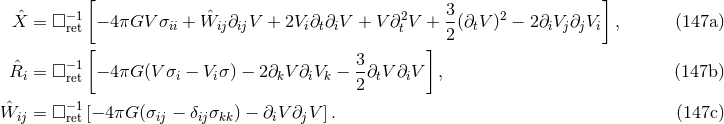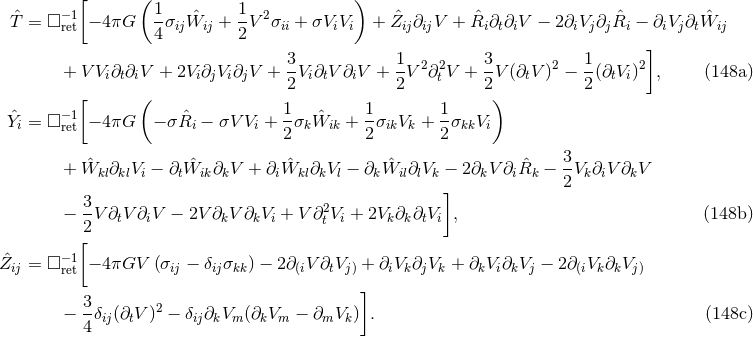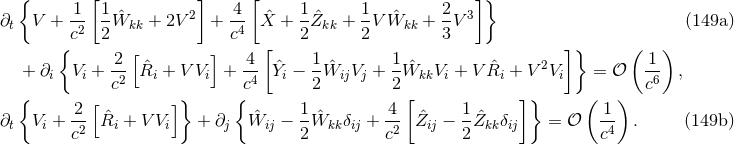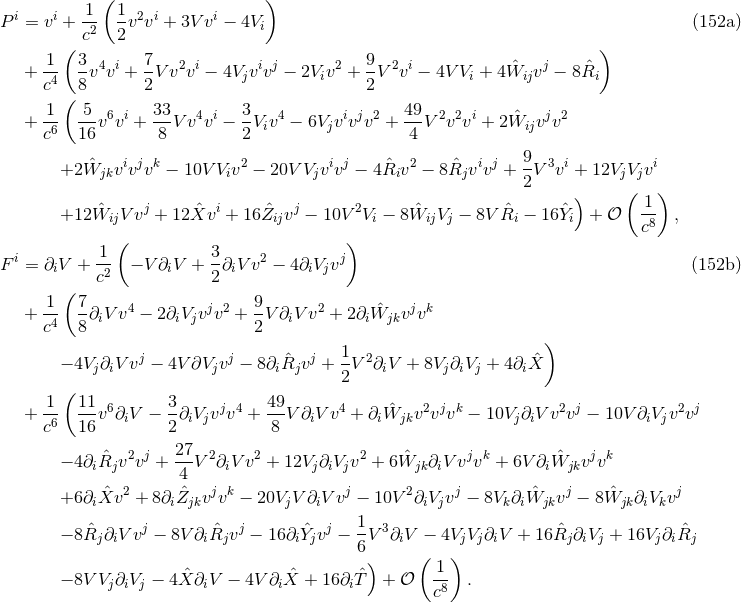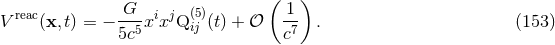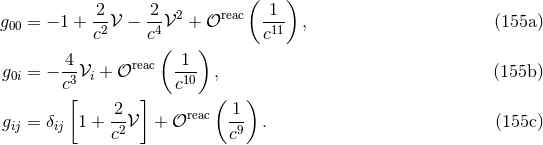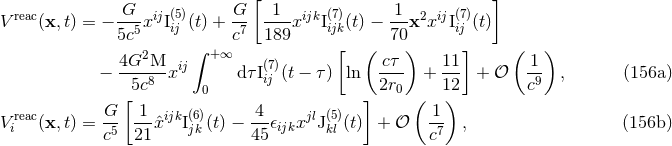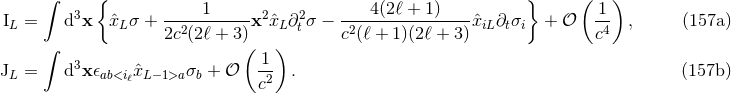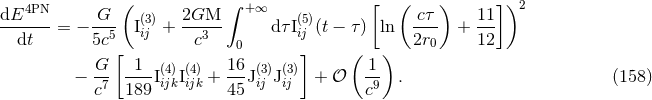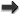5 Interior Field of a Post-Newtonian Source
Theorem 6 solves in principle the question of the generation of gravitational waves by extended post-Newtonian matter sources. However, notice that this result has still to be completed by the precise procedure, i.e., an explicit “algorithm”, for the post-Newtonian iteration of the near-zone field, analogous to the multipolar-post-Minkowskian algorithm we defined in Section 2. Such procedure will permit the systematic computation of the source multipole moments, which contain the full post-Newtonian expansion of the pseudo-tensor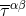 , and of the radiation reaction effects occurring within the matter
source.
, and of the radiation reaction effects occurring within the matter
source.
Before proceeding, let us recall that the “standard” post-Newtonian approximation, as it was used until, say, the early 1980’s (see for instance Refs. [6*, 181*, 269*, 270*, 334*] and also the earlier works [344, 122, 124, 123]), was plagued with some apparently inherent difficulties, which croped up at some high post-Newtonian order. Historically these difficulties, even appearing at higher approximations, have cast a doubt on the actual soundness, from a theoretical point of view, of the post-Newtonian expansion. Practically speaking, they posed the question of the reliability of the approximation, when comparing the theory’s predictions with very precise experimental results. This was one of the main reason for the famous radiation-reaction controversy raging at the time of the binary pulsar data [182, 418]. In this section we assess the nature of these difficulties – are they purely technical or linked with some fundamental drawback of the approximation scheme? – and eventually resolve them.
- The first problem we face is that in higher approximations some divergent Poisson-type integrals
appear. Indeed the post-Newtonian expansion replaces the resolution of a hyperbolic-like
d’Alembertian equation by a perturbatively equivalent hierarchy of elliptic-like Poisson
equations. Rapidly it is found during the post-Newtonian iteration that the right-hand side of
the Poisson equations acquires a non-compact support (it is distributed all over space
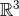 ),
and that as a result the standard Poisson integral diverges at the bound of the integral at
spatial infinity, i.e., when
),
and that as a result the standard Poisson integral diverges at the bound of the integral at
spatial infinity, i.e., when 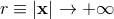 , with
, with 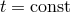 .
.
- The second problem is related with the limitation of the post-Newtonian approximation to the
near zone – the region surrounding the source of small extent with respect to the wavelength
of the emitted radiation:
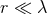 . As we have seen, the post-Newtonian expansion assumes
from the start that all retardations
. As we have seen, the post-Newtonian expansion assumes
from the start that all retardations 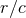 are small, so it can rightly be viewed as a formal
near-zone expansion, when
are small, so it can rightly be viewed as a formal
near-zone expansion, when 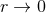 . Note that the fact which makes the Poisson integrals to
become typically divergent, namely that the coefficients of the post-Newtonian series blow up
at spatial infinity, when
. Note that the fact which makes the Poisson integrals to
become typically divergent, namely that the coefficients of the post-Newtonian series blow up
at spatial infinity, when 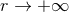 , has nothing to do with the actual behaviour of the field at
infinity. However, the serious consequence is that it is a priori impossible to implement within
the post-Newtonian scheme alone the physical information that the matter system is isolated
from the rest of the Universe. Most importantly, the no-incoming radiation condition, imposed
at past null infinity, cannot be taken directly into account, a priori, into the post-Newtonian
scheme. In this sense the post-Newtonian approximation is not “self-supporting”, because it
necessitates some information taken from outside its own domain of validity.
, has nothing to do with the actual behaviour of the field at
infinity. However, the serious consequence is that it is a priori impossible to implement within
the post-Newtonian scheme alone the physical information that the matter system is isolated
from the rest of the Universe. Most importantly, the no-incoming radiation condition, imposed
at past null infinity, cannot be taken directly into account, a priori, into the post-Newtonian
scheme. In this sense the post-Newtonian approximation is not “self-supporting”, because it
necessitates some information taken from outside its own domain of validity.
The divergencies are linked to the fact that the post-Newtonian expansion is actually a singular
perturbation, in the sense that the coefficients of the successive powers of 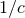 are not uniformly valid
in space, since they typically blow up at spatial infinity like some powers of
are not uniformly valid
in space, since they typically blow up at spatial infinity like some powers of  . We know
for instance that the post-Newtonian expansion cannot be “asymptotically flat” starting at
the 2PN or 3PN level, depending on the adopted coordinate system [362]. The result is that
the standard Poisson integrals are in general badly-behaving at infinity. Trying to solve the
post-Newtonian equations by means of the Poisson integral does not make sense. However, this does not
mean that there are no solutions to the problem, but simply that the Poisson integral does not
constitute the appropriate solution of the Poisson equation in the context of post-Newtonian
expansions.
. We know
for instance that the post-Newtonian expansion cannot be “asymptotically flat” starting at
the 2PN or 3PN level, depending on the adopted coordinate system [362]. The result is that
the standard Poisson integrals are in general badly-behaving at infinity. Trying to solve the
post-Newtonian equations by means of the Poisson integral does not make sense. However, this does not
mean that there are no solutions to the problem, but simply that the Poisson integral does not
constitute the appropriate solution of the Poisson equation in the context of post-Newtonian
expansions.
Here we present, following Refs. [357*, 75*], a solution of both problems, in the form of a general expression for the near-zone gravitational field, developed to any post-Newtonian order, which has been determined from implementing the matching equation (103*). This solution is free of the divergences of Poisson-type integrals we mentioned above, and yields, in particular, some general expression, valid up to any order, of the terms associated with the gravitational radiation reaction force inside the post-Newtonian source.
Though we shall focus our attention on the particular approach advocated in [357*, 75*], there are other ways to resolve the problems of the post-Newtonian approximation. Notably, an alternative solution to the problem of divergencies, proposed in Refs. [214, 211], is based on an initial-value formulation. In this method the problem of the appearance of divergencies is avoided because of the finiteness of the causal region of integration, between the initial Cauchy hypersurface and the considered field point. On the other hand, a different approach to the problem of radiation reaction, which does not use a matching procedure, is to work only within a post-Minkowskian iteration scheme without expanding the retardations, see e.g., Ref. [126].
5.1 Post-Newtonian iteration in the near zone
We perform the post-Newtonian iteration of the field equations in harmonic coordinates in the near zone of
an isolated matter distribution. We deal with a general hydrodynamical fluid, whose stress-energy tensor is
smooth, i.e., 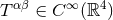 . Thus the scheme a priori excludes the presence of singularities and black
holes; these will be dealt with in Part B of this article.
. Thus the scheme a priori excludes the presence of singularities and black
holes; these will be dealt with in Part B of this article.
We shall now prove [357*] that the post-Newtonian expansion can be indefinitely iterated without
divergences. Like in Eq. (106*) we denote by means of an overline the formal (infinite) post-Newtonian
expansion of the field inside the source’s near-zone. The general structure of the post-Newtonian expansion
is denoted (skipping the space-time indices 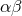 ) as
) as
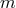 -th post-Newtonian coefficient is naturally the factor of the
-th post-Newtonian coefficient is naturally the factor of the 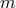 -th power of
-th power of 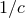 . However, we know
from restoring the factors
. However, we know
from restoring the factors  ’s in Theorem 3 [see Eq. (53*)], that the post-Newtonian expansion also involves
powers of the logarithm of
’s in Theorem 3 [see Eq. (53*)], that the post-Newtonian expansion also involves
powers of the logarithm of  ; these are included for convenience here into the definition of the coefficients
; these are included for convenience here into the definition of the coefficients
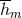 .33
For the stress-energy pseudo-tensor appearing in Eq. (106*) we have the same type of expansion,
Note that the expansion starts with a term of order
.33
For the stress-energy pseudo-tensor appearing in Eq. (106*) we have the same type of expansion,
Note that the expansion starts with a term of order 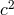 corresponding to the rest mass-energy (
corresponding to the rest mass-energy (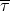 has the
dimension of an energy density). As usual we shall understand the infinite sums such as (127*) – (128*) in the
sense of formal series, i.e., merely as an ordered collection of coefficients. Because of our consideration of
regular extended matter distributions the post-Newtonian coefficients are smooth functions of space-time,
i.e.,
has the
dimension of an energy density). As usual we shall understand the infinite sums such as (127*) – (128*) in the
sense of formal series, i.e., merely as an ordered collection of coefficients. Because of our consideration of
regular extended matter distributions the post-Newtonian coefficients are smooth functions of space-time,
i.e., 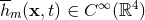 .
.
Inserting the post-Newtonian ansatz (127*) into the harmonic-coordinates Einstein field equation
(21*) – (22*) and equating together the powers of 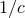 , results is an infinite set of Poisson-type equations
(
, results is an infinite set of Poisson-type equations
(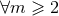 ),
),
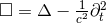 (this term is zero when
(this term is zero when 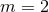 and
and 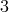 ). We proceed by induction, i.e.,
we work at some given but arbitrary post-Newtonian order
). We proceed by induction, i.e.,
we work at some given but arbitrary post-Newtonian order 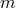 , assume that we succeeded in constructing
the sequence of previous coefficients
, assume that we succeeded in constructing
the sequence of previous coefficients 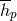 (
(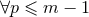 ), and from that show how to infer the next-order
coefficient
), and from that show how to infer the next-order
coefficient 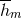 .
.
To cure the problem of divergencies we introduce a generalized solution of the Poisson equation with
non-compact support source, in the form of an appropriate finite part of the usual Poisson integral obtained
by regularization of the bound at infinity by means of a specific process of analytic continuation. For any
source term like 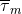 , we multiply it by the regularization factor
, we multiply it by the regularization factor 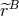 already extensively used in the
construction of the exterior field, thus
already extensively used in the
construction of the exterior field, thus 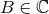 and
and 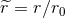 is given by Eq. (42*). Only then do
we apply the usual Poisson integral, which therefore defines a certain function of
is given by Eq. (42*). Only then do
we apply the usual Poisson integral, which therefore defines a certain function of 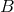 . The
well-definedness of that integral heavily relies on the behaviour of the integrand at the bound at
infinity. There is no problem with the vicinity of the origin inside the source because of the
smoothness of the pseudo-tensor. Then one can prove [357*] that the latter function of
. The
well-definedness of that integral heavily relies on the behaviour of the integrand at the bound at
infinity. There is no problem with the vicinity of the origin inside the source because of the
smoothness of the pseudo-tensor. Then one can prove [357*] that the latter function of 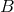 generates
a (unique) analytic continuation down to a neighbourhood of the value of interest
generates
a (unique) analytic continuation down to a neighbourhood of the value of interest 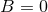 ,
except at
,
except at 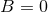 itself, at which value it admits a Laurent expansion with multiple poles up to
some finite order (but growing with the post-Newtonian order
itself, at which value it admits a Laurent expansion with multiple poles up to
some finite order (but growing with the post-Newtonian order 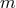 ). Then, we consider the
Laurent expansion of that function when
). Then, we consider the
Laurent expansion of that function when 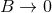 and pick up the finite part, or coefficient of
the zero-th power of
and pick up the finite part, or coefficient of
the zero-th power of 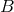 , of that expansion. This defines our generalized Poisson integral:
, of that expansion. This defines our generalized Poisson integral:
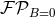 or
or 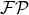 for short. The main properties of this generalized Poisson operator is that it
solves the Poisson equation,
and that the solution
for short. The main properties of this generalized Poisson operator is that it
solves the Poisson equation,
and that the solution 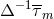 owns the same properties as its source
owns the same properties as its source 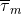 , i.e., the smoothness and the
same type of behaviour at infinity, as given by Eq. (104*). Similarly, we define the generalized iterated
Poisson integral as
, i.e., the smoothness and the
same type of behaviour at infinity, as given by Eq. (104*). Similarly, we define the generalized iterated
Poisson integral as
The most general solution of the Poisson equation will be obtained by application of the previous generalized Poisson operator to the right-hand side of Eq. (129*), and augmented by the most general homogeneous solution of the Poisson equation. Thus, we can write
The last term represents the most general solution of the Laplace equation that is regular at the origin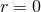 . It can be written in STF guise as a multipolar series of terms of the type
. It can be written in STF guise as a multipolar series of terms of the type
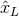 , and multiplied by arbitrary STF-tensorial functions of time
, and multiplied by arbitrary STF-tensorial functions of time 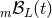 . These functions
will be associated with the radiation reaction of the field onto the source; they will depend on
which boundary conditions are to be imposed on the gravitational field at infinity from the
source.
. These functions
will be associated with the radiation reaction of the field onto the source; they will depend on
which boundary conditions are to be imposed on the gravitational field at infinity from the
source.
It is now trivial to iterate the process. We substitute for 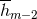 in the right-hand side of Eq. (133*) the
same expression but with
in the right-hand side of Eq. (133*) the
same expression but with 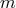 replaced by
replaced by  , and similarly come down until we stop at either one of
the coefficients
, and similarly come down until we stop at either one of
the coefficients 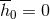 or
or 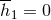 . At this point
. At this point 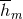 is expressed in terms of the previous
is expressed in terms of the previous 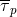 ’s and
’s and
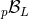 ’s with
’s with 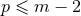 . To finalize the process we introduce what we call the operator of the
“instantaneous” potentials and denote
. To finalize the process we introduce what we call the operator of the
“instantaneous” potentials and denote 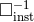 . Our notation is chosen to contrast with the standard
operator of the retarded potentials
. Our notation is chosen to contrast with the standard
operator of the retarded potentials 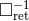 defined by Eq. (31*). However, beware of the fact that unlike
defined by Eq. (31*). However, beware of the fact that unlike
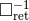 the operator
the operator 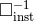 will be defined only when acting on a post-Newtonian series such as
will be defined only when acting on a post-Newtonian series such as 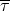 . Indeed,
we pose
. Indeed,
we pose
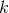 -th iteration of the generalized Poisson operator is defined by Eq. (132*). This
operator is instantaneous in the sense that it does not involve any integration over time. It is
readily checked that in this way we have a solution of the source-free d’Alembertian equation,
On the other hand, the homogeneous solution in Eq. (133*) will yield by iteration an homogeneous solution
of the d’Alembertian equation that is necessarily regular at the origin. Hence it should be of the
anti-symmetric type, i.e., be made of the difference between a retarded multipolar wave and the
corresponding advanced wave. We shall therefore introduce a new definition for some STF-tensorial
functions
-th iteration of the generalized Poisson operator is defined by Eq. (132*). This
operator is instantaneous in the sense that it does not involve any integration over time. It is
readily checked that in this way we have a solution of the source-free d’Alembertian equation,
On the other hand, the homogeneous solution in Eq. (133*) will yield by iteration an homogeneous solution
of the d’Alembertian equation that is necessarily regular at the origin. Hence it should be of the
anti-symmetric type, i.e., be made of the difference between a retarded multipolar wave and the
corresponding advanced wave. We shall therefore introduce a new definition for some STF-tensorial
functions 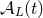 parametrizing those advanced-minus-retarded free waves. It is very easy to relate if
necessary the post-Newtonian expansion of
parametrizing those advanced-minus-retarded free waves. It is very easy to relate if
necessary the post-Newtonian expansion of 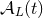 to the functions
to the functions 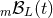 previously introduced in
Eq. (133*). Finally the most general post-Newtonian solution, iterated ad infinitum and without any
divergences, is obtained into the form
We shall refer to the
previously introduced in
Eq. (133*). Finally the most general post-Newtonian solution, iterated ad infinitum and without any
divergences, is obtained into the form
We shall refer to the 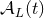 ’s as the radiation-reaction functions. If we stay at the level of the
post-Newtonian iteration which is confined into the near zone we cannot do more than Eq. (136*): There is
no means to compute the radiation-reaction functions
’s as the radiation-reaction functions. If we stay at the level of the
post-Newtonian iteration which is confined into the near zone we cannot do more than Eq. (136*): There is
no means to compute the radiation-reaction functions 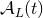 . We are here touching the second problem
faced by the standard post-Newtonian approximation.
. We are here touching the second problem
faced by the standard post-Newtonian approximation.
5.2 Post-Newtonian metric and radiation reaction effects
As we have understood this problem is that of the limitation to the near zone. Such limitation can be
circumvented to the lowest post-Newtonian orders by considering retarded integrals that are formally
expanded when 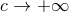 as series of “instantaneous” Poisson-like integrals, see e.g., [6*]. This procedure
works well up to the 2.5PN level and has been shown to correctly fix the dominant radiation
reaction term at the 2.5PN order [181, 269, 270, 334]. Unfortunately such a procedure assumes
fundamentally that the gravitational field, after expansion of all retardations
as series of “instantaneous” Poisson-like integrals, see e.g., [6*]. This procedure
works well up to the 2.5PN level and has been shown to correctly fix the dominant radiation
reaction term at the 2.5PN order [181, 269, 270, 334]. Unfortunately such a procedure assumes
fundamentally that the gravitational field, after expansion of all retardations 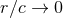 , depends on
the state of the source at a single time
, depends on
the state of the source at a single time 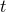 , in keeping with the instantaneous character of
the Newtonian interaction. However, we know that the post-Newtonian field (as well as the
source’s dynamics) will cease at some stage to be given by a functional of the source parameters
at a single time, because of the imprint of gravitational-wave tails in the near zone field, in
the form of the hereditary modification of the radiation reaction force at the 1.5PN relative
order [58*, 60*, 43*]. Since the reaction force is itself of order 2.5PN this means that the formal
post-Newtonian expansion of retarded Green functions is no longer valid starting at the 4PN
order.
, in keeping with the instantaneous character of
the Newtonian interaction. However, we know that the post-Newtonian field (as well as the
source’s dynamics) will cease at some stage to be given by a functional of the source parameters
at a single time, because of the imprint of gravitational-wave tails in the near zone field, in
the form of the hereditary modification of the radiation reaction force at the 1.5PN relative
order [58*, 60*, 43*]. Since the reaction force is itself of order 2.5PN this means that the formal
post-Newtonian expansion of retarded Green functions is no longer valid starting at the 4PN
order.
The solution of the problem resides in the matching of the near-zone field to the exterior field. We have
already seen in Theorems 5 and 6 that the matching equation (103*) yields the expression of the multipole
expansion in the exterior domain. Now we prove that it also permits the full determinantion of the
post-Newtonian metric in the near-zone, i.e., the radiation-reaction functions 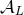 which have been left
unspecified in Eq. (136*).
which have been left
unspecified in Eq. (136*).
We find [357*] that the radiation-reaction functions 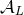 are composed of the multipole moment
functions
are composed of the multipole moment
functions 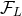 defined by Eq. (119*), which will here characterize “linear-order” radiation reaction effects
starting at 2.5PN order, and of an extra piece
defined by Eq. (119*), which will here characterize “linear-order” radiation reaction effects
starting at 2.5PN order, and of an extra piece 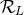 , which will be due to non-linear effets in the radiation
reaction and turn out to arise at the 4PN order. Thus,
, which will be due to non-linear effets in the radiation
reaction and turn out to arise at the 4PN order. Thus,
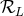 is obtained from the multipole expansion of the pseudo-tensor
is obtained from the multipole expansion of the pseudo-tensor
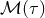 .34
Hence the radiation-reaction functions do depend on the behaviour of the field far away from the matter
source (as physical intuition already told us). The explicit expression reads
The fact that the multipolar expansion
.34
Hence the radiation-reaction functions do depend on the behaviour of the field far away from the matter
source (as physical intuition already told us). The explicit expression reads
The fact that the multipolar expansion 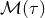 is the source term for the function
is the source term for the function 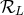 is the consequence
of the matching equation (103*). The specific contributions due to
is the consequence
of the matching equation (103*). The specific contributions due to 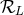 in the post-Newtonian metric (136*)
are associated with tails of waves [58*, 43*]. Notice that, remarkably, the
in the post-Newtonian metric (136*)
are associated with tails of waves [58*, 43*]. Notice that, remarkably, the 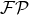 regularization deals with the
bound of the integral at
regularization deals with the
bound of the integral at 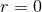 , in contrast with Eq. (119*) where it deals with the bound at
, in contrast with Eq. (119*) where it deals with the bound at
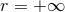 . The weighting function
. The weighting function 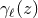 therein, where
therein, where  extends up to infinity in contrast
to the analogous function
extends up to infinity in contrast
to the analogous function 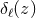 in Eq. (119*), is simply related to it by
in Eq. (119*), is simply related to it by 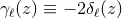 ;
such definition is motivated by the fact that the integral of that function is normalized to
one:35
The post-Newtonian metric (136*) is now fully determined. However, let us now prove a more interesting
alternative formulation of it, derived in Ref. [75*].
;
such definition is motivated by the fact that the integral of that function is normalized to
one:35
The post-Newtonian metric (136*) is now fully determined. However, let us now prove a more interesting
alternative formulation of it, derived in Ref. [75*].
Theorem 7. The expression of the post-Newtonian field in the near zone of a post-Newtonian source, satisfying correct boundary conditions at infinity (no incoming radiation), reads
The first term represents a particular solution of the hierarchy of post-Newtonian equations, while the second one is a homogeneous multipolar solution of the wave equation, of the “anti-symmetric” type that is regular at the origin located inside the source, and parametrized by the multipole-moment functions (138*).
located inside the source, and parametrized by the multipole-moment functions (138*).
Let us be more precise about the meaning of the first term in Eq. (140*). Indeed such term is made of the
formal expansion of the standard retarded integral (31*) when 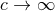 , but acting on a post-Newtonian
source term
, but acting on a post-Newtonian
source term 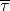 ,
,
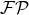 operation in order to
deal with the bound at infinity at which the post-Newtonian expansion is singular. Because
of the presence of this regularization, the object (141*) should carefully be distinguished from
the “global” solution
operation in order to
deal with the bound at infinity at which the post-Newtonian expansion is singular. Because
of the presence of this regularization, the object (141*) should carefully be distinguished from
the “global” solution ![− 1 □ret[τ]](article1137x.gif) defined by Eq. (31*), with global non-expanded pseudo-tensor
defined by Eq. (31*), with global non-expanded pseudo-tensor
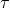 .
.
The definition (141*) is of interest because it corresponds to what one would intuitively think as the natural way of performing the post-Newtonian iteration, i.e., by formally Taylor expanding the retardations in Eq. (31*), as was advocated by Anderson & DeCanio [6]. Moreover, each of the terms of the series (141*) is mathematically well-defined thanks to the finite part operation, and can therefore be implemented in practical computations. The point is that Eq. (141*) solves the wave equation in a perturbative post-Newtonian sense,
so constitutes a good prescription for a particular solution of the wave equation – as legitimate as the solution (134*). Therefore the two solutions should differ by an homogeneous solution of the wave equation which is necessarily of the anti-symmetric type (regular inside the source). Detailed investigations [357*, 75*] yield where the homogeneous solution is parametrized by the multipole-moments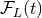 . By combining
Eqs. (140*) and (143*), we indeed become reconciled with the previous expression of the post-Newtonian
field found in Eq. (136*).
. By combining
Eqs. (140*) and (143*), we indeed become reconciled with the previous expression of the post-Newtonian
field found in Eq. (136*).
For computations limited to the 3.5PN order (level of the 1PN correction to the radiation reaction
force), the first term in Eq. (140*) with the “intuitive” prescription (141*) is sufficient. But because of the
second term in (140*) there is a fundamental breakdown of this scheme at the 4PN order where it becomes
necessary to take into account non-linear radiation reaction effects associated with tails. The second term in
(140*) constitutes a generalization of the tail-transported radiation reaction arising at the 4PN order, i.e.,
1.5PN order relative to the dominant radiation reaction order, as determined in Ref. [58*]. The
tail-transported radiation reaction is required by energy conservation and the presence of tails in the
wave zone. The usual radiation reaction terms, up to 3.5PN order, are contained in the first
term of Eq. (140*), and are parametrized by the same multipole-moment functions 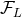 as
the exterior multipolar field, as Eq. (143*) explicitly shows. In Section 5.4 we shall give an
explicit expression of the radiation reaction force showing the usual radiation reaction terms to
3.5PN order, issued from
as
the exterior multipolar field, as Eq. (143*) explicitly shows. In Section 5.4 we shall give an
explicit expression of the radiation reaction force showing the usual radiation reaction terms to
3.5PN order, issued from 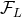 , and exhibiting the above tail-induced 4PN effect, issued from
, and exhibiting the above tail-induced 4PN effect, issued from
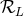 .
.
Finally note that the post-Newtonian solution, in either form (136*) or (140*), has been obtained without imposing the condition of harmonic coordinates (21*) in an explicit way. We have simply matched together the post-Newtonian and multipolar expansions, satisfying the “relaxed” Einstein field equations (22*) in their respective domains, and found that the matching determines uniquely the solution. An important check done in [357, 75], is therefore to verify that the harmonic coordinate condition (21*) is indeed satisfied as a consequence of the conservation of the pseudo-tensor (27*), so that we really grasp a solution of the full Einstein field equations.
5.3 The 3.5PN metric for general matter systems
The detailed calculations that are called for in applications necessitate having at one’s disposal some
explicit expressions of the metric coefficients 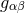 , in harmonic coordinates, at the highest possible
post-Newtonian order. The 3.5PN metric that we present below can be viewed as an application of the
formalism of the previous section. It is expressed by means of some particular retarded-type potentials,
, in harmonic coordinates, at the highest possible
post-Newtonian order. The 3.5PN metric that we present below can be viewed as an application of the
formalism of the previous section. It is expressed by means of some particular retarded-type potentials, 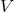 ,
,
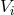 ,
, 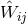 , …, whose main advantages are to somewhat minimize the number of terms, so that even at the
3.5PN order the metric is still tractable, and to delineate the different problems associated with
the computation of different categories of terms. Of course, these potentials have no direct
physical significance by themselves, but they offer a convenient parametrization of the 3.5PN
metric.
, …, whose main advantages are to somewhat minimize the number of terms, so that even at the
3.5PN order the metric is still tractable, and to delineate the different problems associated with
the computation of different categories of terms. Of course, these potentials have no direct
physical significance by themselves, but they offer a convenient parametrization of the 3.5PN
metric.
The basic idea in our post-Newtonian iteration scheme is to use wherever possible a “direct” integration,
with the help of some formulas like 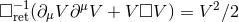 . The 3.5PN harmonic-coordinates
metric reads [71*]
. The 3.5PN harmonic-coordinates
metric reads [71*]
All the potentials are generated by the matter stress-energy tensor 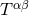 through some convenient
definitions recalling Eqs. (124),
through some convenient
definitions recalling Eqs. (124),
Starting at Newtonian and 1PN orders, 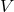 and
and 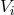 represent some retarded versions of the usual
Newtonian and gravitomagnetic potentials,
represent some retarded versions of the usual
Newtonian and gravitomagnetic potentials,
From the 2PN order we have the potentials
Some parts of these potentials are directly generated by compact-support matter terms, while other
parts are made of non-compact-support products of 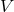 -type potentials. There exists also an
important cubically non-linear term generated by the coupling between
-type potentials. There exists also an
important cubically non-linear term generated by the coupling between 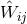 and
and 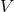 , see the
second term in the
, see the
second term in the 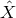 -potential. Note the important point that here and below the retarded
integral operator
-potential. Note the important point that here and below the retarded
integral operator 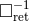 is really meant to be the one given by Eq. (141*); thus it involves in
principle the finite part regularization
is really meant to be the one given by Eq. (141*); thus it involves in
principle the finite part regularization 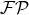 to deal with (IR-type) divergences occurring at
high post-Newtonian orders for non-compact-support integrals. For instance, such finite part
regularization is important to take into account in the computation of the near zone metric at the 3PN
order [68*].
to deal with (IR-type) divergences occurring at
high post-Newtonian orders for non-compact-support integrals. For instance, such finite part
regularization is important to take into account in the computation of the near zone metric at the 3PN
order [68*].
At the next level, 3PN, we have even more complicated potentials, namely
These involve many types of compact-support contributions, as well as quadratic-order and cubic-order
parts; but, surprisingly, there are no quartically non-linear terms. Indeed it has been possible to “integrate
directly” all the quartic contributions in the 3PN metric; see the terms composed of 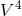 and
and 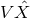 in the
first of Eqs. (144).
in the
first of Eqs. (144).
Note that the 3PN metric (144) does represent the inner post-Newtonian field of an isolated system, because it contains, to this order, the correct radiation-reaction terms corresponding to outgoing radiation. These terms come from the expansions of the retardations in the retarded potentials (146) – (148); we elaborate more on radiation-reaction effects in the next Section 5.4.
The above potentials are not independent: They are linked together by some differential identities issued from the harmonic gauge conditions, which are equivalent, via the Bianchi identities, to the equations of motion of the matter fields; see Eq. (27*). These identities read
For latter applications to systems of compact objects, let us give the geodesic equations of a particle moving in the 3.5PN metric (144).36 It is convenient to write these equations as
where the “linear momentum density”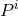 and the “force density”
and the “force density” 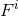 of the particle are given by
of the particle are given by
where 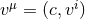 with
with 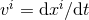 being the particle’s ordinary coordinate velocity, and
where the metric components are taken at the location of the particle. Notice that we are here
viewing the particle as moving in the fixed background metric (144). In Part B of this article, the
metric will be generated by the system of particles itself, and we shall have to supplement
the computation of the metric at the location of one of these particles by a suitable self-field
regularization.
being the particle’s ordinary coordinate velocity, and
where the metric components are taken at the location of the particle. Notice that we are here
viewing the particle as moving in the fixed background metric (144). In Part B of this article, the
metric will be generated by the system of particles itself, and we shall have to supplement
the computation of the metric at the location of one of these particles by a suitable self-field
regularization.
The expressions of both 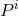 and
and 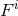 in terms of the non-linear potentials follow from insertion of the
3.5PN metric coefficients (144). We obtain some complicated-looking (but useful in applications) sums of
products of potentials given by
in terms of the non-linear potentials follow from insertion of the
3.5PN metric coefficients (144). We obtain some complicated-looking (but useful in applications) sums of
products of potentials given by
Note that it will be supposed that all the accelerations appearing in the potentials and in the final
expression of the equations of motion are order-reduced by means of the equations of motion
themselves. For instance, we see from Eq. (152a) that when computing the time-derivative of 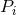 we
shall meet an acceleration at 1PN order which is therefore to be replaced by the explicit 2.5PN
equations of motion. The order-reduction is a crucial aspect of the post-Newtonian method. It is
justified by the fact that the matter equations of motion, say
we
shall meet an acceleration at 1PN order which is therefore to be replaced by the explicit 2.5PN
equations of motion. The order-reduction is a crucial aspect of the post-Newtonian method. It is
justified by the fact that the matter equations of motion, say 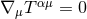 , represent four out of
the ten Einstein field equations, see Section 2.1 for discussion. In the harmonic-coordinate
approach the equations of motion are equivalent to the harmonic gauge conditions
, represent four out of
the ten Einstein field equations, see Section 2.1 for discussion. In the harmonic-coordinate
approach the equations of motion are equivalent to the harmonic gauge conditions 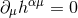 .
Thus, each time we get an acceleration in some PN expression (including the PN expression
of the acceleration itself), we have also another equation (or the same equation) which tells
that the acceleration is given by another PN expression. The post-Newtonian method assumes
that it is legitimate to replace that acceleration and to re-expand consistently with the PN
order. Post-Newtonian predictions based on such consistent PN order-reduction have been very
successful.37
.
Thus, each time we get an acceleration in some PN expression (including the PN expression
of the acceleration itself), we have also another equation (or the same equation) which tells
that the acceleration is given by another PN expression. The post-Newtonian method assumes
that it is legitimate to replace that acceleration and to re-expand consistently with the PN
order. Post-Newtonian predictions based on such consistent PN order-reduction have been very
successful.37
5.4 Radiation reaction potentials to 4PN order
We said that the metric (144) contains the correct radiation-reaction terms appropriate for an isolated
system up to the 3.5PN level included. The metric can even be generalized to include the radiation-reaction
terms up to 4PN order. To show this we shall use a particular non-harmonic coordinate system to describe
the radiation reaction terms up to 4PN order, which constitutes a natural generalization of the Burke &
Thorne [114, 113] coordinate system at 2.5PN order. Recall that at the lowest 2.5PN order the radiation
reaction force takes the simple form of Eq. (6*), in which the force 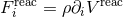 involves only a scalar
potential given by
involves only a scalar
potential given by
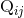 is
simply given by the usual Newtonian expression (3*).
is
simply given by the usual Newtonian expression (3*).
The novel feature when one extends the Newtonian radiation reaction to include the 1PN corrections is that the reaction force is no longer composed of a single scalar depending on the mass-type multipole moments, but involves also a vectorial component depending in particular on the current-type quadrupole moment. This was noticed in the physically restricted case where the dominant quadrupolar radiation from the source is suppressed [56]. The vectorial component of the reaction force could be important in some astrophysical situations like rotating neutron stars undergoing gravitational instabilities. Here we report the results of the extension to 1.5PN order of the lowest-order Burke & Thorne scalar radiation reaction potential (153*), in some appropriate coordinate system, following Refs. [43*, 47*].
At that level (corresponding to 4PN order in the metric), and in this particular coordinate system, it
suffices to incorporate some radiation-reaction contributions into the scalar and vectorial potentials 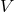 and
and 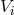 which parametrize the metric in Eq. (144). We thus pose
which parametrize the metric in Eq. (144). We thus pose
Then the metric, accurate to 4PN order regarding the radiation-reaction contributions – we indicate this
by using the symbol 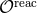 for the remainders – reads
for the remainders – reads
The other contributions, which are conservative (i.e., non radiative), are given up to 3PN order by
the metric (144) in which all the potentials take the same form as in Eqs. (146) – (148), but
where one neglects all the retardations, which means that the retarded integral operator 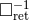 should be replaced by the operator of the instantaneous potentials
should be replaced by the operator of the instantaneous potentials 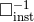 defined by Eq. (134*).
This is for instance what we have indicated in Eqs. (154) by writing
defined by Eq. (134*).
This is for instance what we have indicated in Eqs. (154) by writing 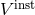 and
and 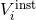 . Up
to 3.5PN order, in this particular coordinate system, the effect of all these retardations gets
replaced by the effect of the radiation-reaction potentials
. Up
to 3.5PN order, in this particular coordinate system, the effect of all these retardations gets
replaced by the effect of the radiation-reaction potentials 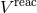 and
and 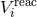 ; furthermore, at the
4PN order there is a modification of the scalar radiation-reaction potential that is imposed by
gravitational-wave tails propagating in the wave zone [58]. The explicit form of these potentials
is [43*, 47*]38
; furthermore, at the
4PN order there is a modification of the scalar radiation-reaction potential that is imposed by
gravitational-wave tails propagating in the wave zone [58]. The explicit form of these potentials
is [43*, 47*]38
where the multipole moments 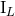 and
and 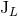 denote the source multipole moments defined in
Eqs. (123). Witness the tail integral at 4PN order characterized by a logarithmic kernel; see
Section 3.2.
denote the source multipole moments defined in
Eqs. (123). Witness the tail integral at 4PN order characterized by a logarithmic kernel; see
Section 3.2.
The scalar potential 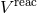 will obviously reproduce Eq. (153*) at the dominant order. However, note
that it is crucial to include in Eq. (156a) the 1PN correction in the source quadrupole moment
will obviously reproduce Eq. (153*) at the dominant order. However, note
that it is crucial to include in Eq. (156a) the 1PN correction in the source quadrupole moment 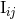 . The
mass-type moments
. The
mass-type moments 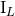 to 1PN order (and the current-type
to 1PN order (and the current-type 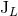 to Newtonian order), read
to Newtonian order), read
The matter source densities 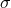 and
and 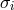 are given in Eqs. (145). Note that the mass multipole
moments
are given in Eqs. (145). Note that the mass multipole
moments 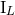 extend only over the compact support of the source even at the 1PN order. Only at the 2PN
order will they involve some non-compact supported contributions – i.e., some integrals extending up to
infinity [44].
extend only over the compact support of the source even at the 1PN order. Only at the 2PN
order will they involve some non-compact supported contributions – i.e., some integrals extending up to
infinity [44].
The 3.5PN radiation reaction force in the equations of motion of compact binary systems has been derived by Iyer & Will [258*, 259*] in an arbitrary gauge, based on the energy and angular momentum balance equations at the relative 1PN order. As demonstrated in Ref. [259*] the expressions of the radiation scalar and vector radiation-reaction potentials (156), which are valid in a particular gauge but are here derived from first principles, are fully consistent with the works [258*, 259*].
With the radiation-reaction potentials (156) in hands, one can prove [47*] the energy balance equation up to 1.5PN order, namely
One recognizes in the right-hand side the known positive-definite expression for the energy
flux at 1.5PN order. Indeed the effective quadrupole moment which appears in the parenthesis
of (158) agrees with the tail-modified radiative quadrupole moment 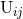 parametrizing the field
in the far zone; see Eq. (90) where we recall that
parametrizing the field
in the far zone; see Eq. (90) where we recall that 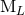 and
and 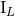 are identical up to 2.5PN
order.
are identical up to 2.5PN
order.


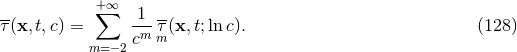

 ≡ − ---ℱ 𝒫B=0 ------′-^r τm(x ,t). (130 ) 4π |x − x |](article1072x.gif)
![( − 1 --) -- Δ Δ [τm] = τm , (131 )](article1075x.gif)
 ≡ − 4π ℱ 𝒫B=0 d x (2k )! ^r τm(x ,t). (132 )](article1078x.gif)
![+ ∞ -- − 1 -- 2 −1 -- ∑ hm = 16πG Δ [mτ−4] + ∂tΔ [mh− 2] + ℬm L(t)ˆxL. (133 ) ℓ=0](article1079x.gif)
![+∑∞ ( )2k □ −1[τ] ≡ -∂-- Δ− k−1[τ-], (134 ) inst c∂t k=0](article1097x.gif)
![( −1 --) -- □ □ inst[τ ] = τ. (135 )](article1099x.gif)
![-- +∑∞ ℓ { } h = 16πG-□ −i1nst[τ] − 4G (− )-∂ˆL 𝒜L-(t −-r-∕c) −-𝒜L-(t-+-r∕c) . (136 ) c4 c4 ℓ=0 ℓ! 2r](article1103x.gif)

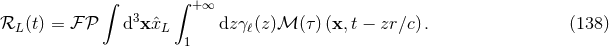

![-- +∑∞ ℓ { αβ αβ } h αβ = 16πG--□− 1[ταβ] − 4G- (−-)-ˆ∂L ℛ-L-(t −-r∕c-) −-ℛ-L-(t +-r∕c) . (140 ) c4 ret c4 ℓ! 2r ℓ=0](article1131x.gif)
 ≡ − --- ------ ---- ℱ𝒫 d3x ′|x − x′|m−1ταβ (x ′,t). (141 ) 4π m=0 m! c∂t](article1135x.gif)
![( −1 -αβ ) -αβ □ □ ret[τ ] = τ , (142 )](article1139x.gif)
![{ } −1 -αβ −1 -αβ 1 +∑ ∞ (− )ℓ ℱ αLβ(t − r∕c) − ℱLαβ(t + r∕c) □ ret[τ ] = □ inst[τ ] − --- -----ˆ∂L ---------------------------- , (143 ) 4π ℓ=0 ℓ! 2r](article1140x.gif)