Our notation is the following: 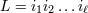 denotes a multi-index, made of
denotes a multi-index, made of 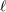 (spatial) indices. Similarly, we write for
instance
(spatial) indices. Similarly, we write for
instance 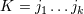 (in practice, we generally do not need to write explicitly the “carrier” letter
(in practice, we generally do not need to write explicitly the “carrier” letter 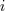 or
or 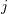 ), or
), or
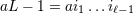 . Always understood in expressions such as Eq. (34) are
. Always understood in expressions such as Eq. (34) are 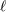 summations over the indices
summations over the indices 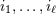 ranging from 1 to 3. The derivative operator
ranging from 1 to 3. The derivative operator 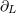 is a short-hand for
is a short-hand for 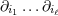 . The function
. The function 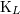 (for any space-time
indices
(for any space-time
indices 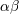 ) is symmetric and trace-free (STF) with respect to the
) is symmetric and trace-free (STF) with respect to the 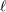 indices composing
indices composing 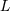 . This means that for any pair
of indices
. This means that for any pair
of indices 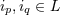 , we have
, we have 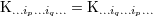 and that
and that 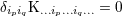 (see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so
(see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so  , or sometimes with carets around the indices,
, or sometimes with carets around the indices, 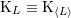 . In particular,
. In particular, 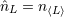 is the
STF projection of the product of unit vectors
is the
STF projection of the product of unit vectors 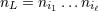 , for instance
, for instance 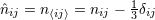 and
and
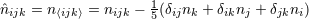 ; an expansion into STF tensors
; an expansion into STF tensors 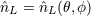 is equivalent to the usual
expansion in spherical harmonics
is equivalent to the usual
expansion in spherical harmonics 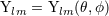 , see Eqs. (75) below. Similarly, we denote
, see Eqs. (75) below. Similarly, we denote 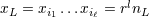 where
where
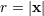 , and
, and ![ˆxL = x⟨L⟩ = STF [xL]](article273x.gif) . The Levi-Civita antisymmetric symbol is denoted
. The Levi-Civita antisymmetric symbol is denoted 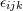 (with
(with 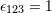 ).
Parenthesis refer to symmetrization,
).
Parenthesis refer to symmetrization, 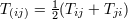 . Superscripts
. Superscripts 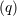 indicate
indicate 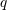 successive time
derivations.
successive time
derivations.
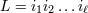 denotes a multi-index, made of
denotes a multi-index, made of 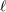 (spatial) indices. Similarly, we write for
instance
(spatial) indices. Similarly, we write for
instance 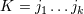 (in practice, we generally do not need to write explicitly the “carrier” letter
(in practice, we generally do not need to write explicitly the “carrier” letter 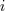 or
or 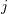 ), or
), or
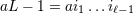 . Always understood in expressions such as Eq. (34*) are
. Always understood in expressions such as Eq. (34*) are 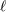 summations over the indices
summations over the indices 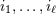 ranging from 1 to 3. The derivative operator
ranging from 1 to 3. The derivative operator 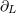 is a short-hand for
is a short-hand for 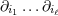 . The function
. The function 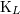 (for any space-time
indices
(for any space-time
indices 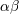 ) is symmetric and trace-free (STF) with respect to the
) is symmetric and trace-free (STF) with respect to the 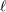 indices composing
indices composing 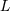 . This means that for any pair
of indices
. This means that for any pair
of indices 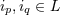 , we have
, we have 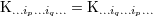 and that
and that 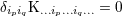 (see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so
(see Ref. [403*] and
Appendices A and B in Ref. [57*] for reviews about the STF formalism). The STF projection is denoted with a hat,
so  , or sometimes with carets around the indices,
, or sometimes with carets around the indices, 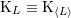 . In particular,
. In particular, 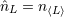 is the
STF projection of the product of unit vectors
is the
STF projection of the product of unit vectors 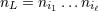 , for instance
, for instance 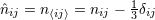 and
and
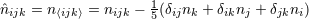 ; an expansion into STF tensors
; an expansion into STF tensors 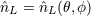 is equivalent to the usual
expansion in spherical harmonics
is equivalent to the usual
expansion in spherical harmonics 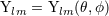 , see Eqs. (75) below. Similarly, we denote
, see Eqs. (75) below. Similarly, we denote 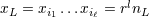 where
where
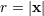 , and
, and ![ˆxL = x⟨L⟩ = STF [xL]](article273x.gif) . The Levi-Civita antisymmetric symbol is denoted
. The Levi-Civita antisymmetric symbol is denoted 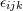 (with
(with 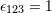 ).
Parenthesis refer to symmetrization,
).
Parenthesis refer to symmetrization, 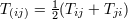 . Superscripts
. Superscripts 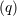 indicate
indicate 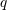 successive time
derivations.
successive time
derivations.