11 Higher-Dimensional Theories Generalizing Kaluza’s
11.1 5-dimensional theories: Jordan–Thiry theory
In January 1950, Yves Thiry submitted a thesis to the faculty of science
of Paris University with the title “Mathematical study of the equations of a unitary theory
with fifteen field variables”. He exuberantly thanked his “master and friend Lichnerowicz” who
obviously had initiated the work. Unfortunately, “Jordan and his school” had “obtained almost at
the same time like us the equations which we will give in Chapter II. We had no knowledge
about this except at a very late stage, and it is only recently that we could correspond with
Jordan. He was so friendly as to send us his publications which we could not have procured
otherwise.”227 ([606*], p. 6) In fact, it was A. Lichnerowicz, then at the university of Strasbourg, who had written to
W. Pauli and asked for “Jordan’s original paper” (cf. letter of W. Pauli to P. Jordan of 23. 3. 1948 in
[489*], p. 516). According to Pauli:
([606*], p. 6) In fact, it was A. Lichnerowicz, then at the university of Strasbourg, who had written to
W. Pauli and asked for “Jordan’s original paper” (cf. letter of W. Pauli to P. Jordan of 23. 3. 1948 in
[489*], p. 516). According to Pauli:
“Lichnerowicz is a pure mathematician who is occupied with the integration of Einstein’s
field equations. One of his students, Ives Thiry now has looked into the (not mutilated)
Kaluza-theory (with 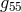 ) and, so I believe, has simplified very much the calculational
technique.”228
) and, so I believe, has simplified very much the calculational
technique.”228
“As to unitary field theories, it seems that their mathematical study has been quite
neglected […]. We thought it useful to try a systematic mathematical study of a unitary
field theory, and to find out whether such a theory is able to present the same coherence
like general relativity.” ([606*], p. 3)232
Thiry’s thesis laid out in three chapters the conceptual background of a 5-dimensional theory, the setting up
and study of the field equations by help of Cartan’s differential calculus, and results on regular solutions of
the theory’s field equations. Unlike in the approach by Einstein & Bergmann (cf. Section 3.2), throughout,
the cylinder condition 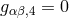 is upheld. Here, he used an argument from physics: no physical
phenomena furnishes evidence for the existence of a fifth dimension ([606*], p. 39). His access to
5-dimensional space made use of the fact that the equations of motion of charged particles are geodesics in
Finsler geometry; for each value of
is upheld. Here, he used an argument from physics: no physical
phenomena furnishes evidence for the existence of a fifth dimension ([606*], p. 39). His access to
5-dimensional space made use of the fact that the equations of motion of charged particles are geodesics in
Finsler geometry; for each value of 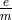 (charge over mass) another Finsler space is needed with the metric:
(charge over mass) another Finsler space is needed with the metric:
“The introduction of a fifth coordinate […] thus shall justify itself by the fact that it imparts
the role of geodesics to the trajectories of charged particles which they lost in space-time
[…]”234
In the third chapter, Thiry aimed at showing that his unitary field theory possessed the same mathematical coherence with regard to its global aspects as general relativity. By partially using methods developed by Lichnerowicz, he proved theorems on the global regularity of solutions such as: “A unitary field with normal asymptotic behavior (i.e., tending uniformly to Minkowski space at spatial infinity) cannot be regular everywhere.” Thiry compared the proofs on the existence and regularity of solutions in O. Klein’s version of Kaluza’s theory and in his generalization and found them much simpler in his theory. These results are of a different nature than what Jordan had achieved; they are new and mathematically exact.
Yet Jordan was not in a hurry to read Thiry’s thesis; he wrote to Pauli:
“By the way, in his thèse published in 1951, Thiry has studied systematically and extensively the theory with variable gravitational constant; […] I received it only after my book appeared and, at present, I have not read it very closely. It thus is not really clear to me whether it contains interesting novelties.” ([490*], p. 799/800)235
To Pauli, Thiry’s global theorems might not have been “interesting novelties”, because in his corresponding paper with Einstein on the non-regularity of solutions, the proof had been independent of the dimension of space [177]. Pauli, at first, also did not read Thiry’s thèse, but responded arrogantly:
“The Thèses by Thiry are laying on my desk; however they are so appallingly thick
(do not contain a reasonable abstract) such that it is so much simpler to not open the
book and reflect about what must be inside.” (W. Pauli to P. Jordan 8. 6. 1953, [491*],
p. 176)236
Somewhat later, Pauli corrected himself and wrote to Jordan that in the preparation for a course “he nevertheless had read around in Thiry’s Thèse” W. Pauli to P. Jordan 3 February 1954 ([491*], p. 442). Note that neither of these two eminent theoretical physicists discussed Thiry’s paper as regards its valuable content.
As to the field equations corresponding to (112*) to (114*), Thiry had calculated them in great detail with
Cartan’s repère mobile for both a Euclidean or Lorentz metric of 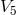 , and also with a 5-dimensional
matter tensor of the form of dust
, and also with a 5-dimensional
matter tensor of the form of dust 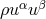 . From the 15th equation, he even had obtained “a new physical
effect”: uncharged dust-matter could generate an electromagnetic field [[606*], p. 79, footnote (1)]. He
linked this effect to Blackett’s search for the magnetic field of a rotating body, described in
Section 6.1.2. As to the interpretation of the fifteenth variable, the scalar field denoted by
. From the 15th equation, he even had obtained “a new physical
effect”: uncharged dust-matter could generate an electromagnetic field [[606*], p. 79, footnote (1)]. He
linked this effect to Blackett’s search for the magnetic field of a rotating body, described in
Section 6.1.2. As to the interpretation of the fifteenth variable, the scalar field denoted by
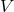 : for him
: for him 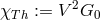 with
with 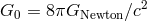 was the gravitational coupling factor
(“facteur de gravitation”) and put in front of the matter tensor [606*], p. 72, 75, 77). In 1951,
Y. Fourès-Bruhat proved existence and uniqueness theorems of “the unitary theory of Jordan–Thiry”
[216, 218].
was the gravitational coupling factor
(“facteur de gravitation”) and put in front of the matter tensor [606*], p. 72, 75, 77). In 1951,
Y. Fourès-Bruhat proved existence and uniqueness theorems of “the unitary theory of Jordan–Thiry”
[216, 218].
11.1.1 Scientists working at the IHP on the Jordan–Thiry unified field theory
Further investigation of the “5-dimensional unitary theory of Jordan–Thiry” as it was named by
Lichnerowicz’ and, later, by Thiry’s students, resulted in several doctoral theses. In one such by Françoise
Hennequin-Guyon, after approximation methods parametrized by 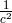 had been developed by her for
the equations of motion in general relativity, they then were applied to Jordan–Thiry theory.
A metric conformally related to the metric induced from the 5-dimensional space
had been developed by her for
the equations of motion in general relativity, they then were applied to Jordan–Thiry theory.
A metric conformally related to the metric induced from the 5-dimensional space 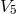 was
introduced such that the gravitational coupling function of the theory became a constant. The first
approximation of a solution was then calculated [254*]. Although stating that her interpretation via the
conformal metric did agree with Jordan’s view (p. 77 of her thesis), surprisingly she did not
mention his book in her bibliography. Like Y. Thiry, in the general formalism F. Hennequin
also considered the “interior” case with a matter tensor by postulating field equation in
was
introduced such that the gravitational coupling function of the theory became a constant. The first
approximation of a solution was then calculated [254*]. Although stating that her interpretation via the
conformal metric did agree with Jordan’s view (p. 77 of her thesis), surprisingly she did not
mention his book in her bibliography. Like Y. Thiry, in the general formalism F. Hennequin
also considered the “interior” case with a matter tensor by postulating field equation in 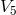
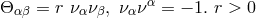 later was called “pseudo-density”,
later was called “pseudo-density”, 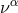 is the 5-velocity. After the projection of the formalism into
space-time, the electromagnetic and the scalar field, named
is the 5-velocity. After the projection of the formalism into
space-time, the electromagnetic and the scalar field, named 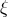 , appeared. The conformal metric mentioned
above is
, appeared. The conformal metric mentioned
above is 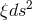 with
with 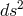 being the metric induced in space-time from
being the metric induced in space-time from 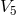 . Electromagnetic field
. Electromagnetic field 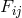 and induction
and induction 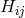 are assumed to be related by
are assumed to be related by 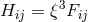 . Hennequin differed from Thiry by giving
as ratio of charge and mass the expression
. Hennequin differed from Thiry by giving
as ratio of charge and mass the expression 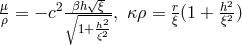 with
with 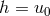 being the
timelike component of the 5-velocity and
being the
timelike component of the 5-velocity and 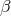 a constant ([254], p. 53), while Thiry had had
a constant ([254], p. 53), while Thiry had had
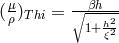 ([606*], p. 78). Her interpretation of the scalar field was also different from the one given
by Lichnerowicz (cf. the end of Section 10.5).
([606*], p. 78). Her interpretation of the scalar field was also different from the one given
by Lichnerowicz (cf. the end of Section 10.5).
In two subsequent theses of 1962 written by Robert Vallée and Pierre Pigeaud the defense of which was
separated by only 4 months, Hennequin’s research within 5-dimensional theory was continued
and generalized to charged perfect fluids. The study of such fluids had been begun by Roland
Guy who extended Lichnerowicz’s results in relativistic
hydrodynamics to “the formalism of the 5-dimensional unitary theories”. His matter tensor included
“pressure” 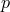 :
: 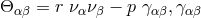 is the 5-dimensional Lorentz metric. His study of the
congruences of the fluid’s streamlines comprised those with rotation: a “tenseur de tourbillon”
is the 5-dimensional Lorentz metric. His study of the
congruences of the fluid’s streamlines comprised those with rotation: a “tenseur de tourbillon”
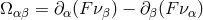 was introduced by R. Guy which after projection to
was introduced by R. Guy which after projection to 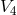 took the form:
took the form:
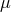 stands for electric charge,
stands for electric charge, 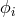 for the electromagnetic 4-potential, and
for the electromagnetic 4-potential, and 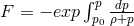 where
where
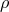 is the mass density.
P. Pigeaud used two metrics, the “natural” one
is the mass density.
P. Pigeaud used two metrics, the “natural” one 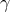 following from the projection of
following from the projection of 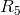 to
to 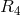 , and
another one conformal to it
, and
another one conformal to it 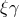 . The first is employed for the calculation of the potentials (up to 2nd
approximation), the 2nd for the study of the equations of motion. The reason is that for the “natural”
metric uncharged test particles do not follow geodesics, yet for the conformal metric they do. At some point,
Pigeaud had to make an ad hoc change of the energy-momentum tensor of matter (perfect fluid) not
justified by empirical physics [495*]. In a later development, Pigeaud did interpret the scalar
fifteenth field variable as the field of a massive meson [387, 496]. The investigations within
Jordan–Thiry theory were carried on by Aline Surin-Parlange to the case of perfect fluid matter with
an equation of state
. The first is employed for the calculation of the potentials (up to 2nd
approximation), the 2nd for the study of the equations of motion. The reason is that for the “natural”
metric uncharged test particles do not follow geodesics, yet for the conformal metric they do. At some point,
Pigeaud had to make an ad hoc change of the energy-momentum tensor of matter (perfect fluid) not
justified by empirical physics [495*]. In a later development, Pigeaud did interpret the scalar
fifteenth field variable as the field of a massive meson [387, 496]. The investigations within
Jordan–Thiry theory were carried on by Aline Surin-Parlange to the case of perfect fluid matter with
an equation of state 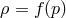 where
where 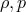 are mass density and pressure, f is an arbitrary
function. The Cauchy problem for this case was solved, the existence of hydrodynamical waves
shown, and their propagation velocity determined. A. Surin compared both, the “singularity”
method and the method using the vanishing of the divergence of the matter tensor in 1st order
approximation: they gave the same results. Unlike F. Hennequin who had assumed for the metric
components237
that
are mass density and pressure, f is an arbitrary
function. The Cauchy problem for this case was solved, the existence of hydrodynamical waves
shown, and their propagation velocity determined. A. Surin compared both, the “singularity”
method and the method using the vanishing of the divergence of the matter tensor in 1st order
approximation: they gave the same results. Unlike F. Hennequin who had assumed for the metric
components237
that 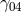 and
and 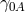 are of the same order
are of the same order 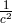 , A. Surin assumed
, A. Surin assumed 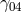 of order
of order 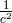 , and
, and
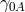 of the order
of the order 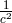 . Unfortunately, as in previous work, the resulting equation of motion for
charged particles still were in conflict with the classical electrodynamic equations. Surin thus
had to change her choice of metric to a conformal metric in space-time; she found that the
equations of motion in first approximation are independent of the conformal metric. Nevertheless,
she had to admit that this did not help: “These last results, particularly those concerning the
first approximation to the equations of motion seem to necessitate a modification of the field
equations.”238
. Unfortunately, as in previous work, the resulting equation of motion for
charged particles still were in conflict with the classical electrodynamic equations. Surin thus
had to change her choice of metric to a conformal metric in space-time; she found that the
equations of motion in first approximation are independent of the conformal metric. Nevertheless,
she had to admit that this did not help: “These last results, particularly those concerning the
first approximation to the equations of motion seem to necessitate a modification of the field
equations.”238 ([597], thèse , p. 126). A. Surin went on to calculate the 2nd approximation, an arduous
task indeed, but which did not make the theory physically more acceptable. Moreover, in 2nd
approximation, as in general relativity the results from both methods did not agree. Surin noted, that a
modification of the field equations already had been suggested by H. Leutwyler [360], but did
not comment on it. He had started from a variational principle mixing 5- and 4-dimensional
quantities:
([597], thèse , p. 126). A. Surin went on to calculate the 2nd approximation, an arduous
task indeed, but which did not make the theory physically more acceptable. Moreover, in 2nd
approximation, as in general relativity the results from both methods did not agree. Surin noted, that a
modification of the field equations already had been suggested by H. Leutwyler [360], but did
not comment on it. He had started from a variational principle mixing 5- and 4-dimensional
quantities:
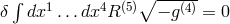 , where
, where 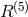 is the 5-dimensional curvature scalar expressible, due to the
cylindricity condition, by quantities in space-time. He claimed to have removed the additional terms which
precluded the derivation of the correct equations of motion. We will briefly present the further dissertation
of R. Vallée below in Section 11.2.1. Huyen Dangvu also studied Jordan–Thiry theory and disagreed with
its interpretation by Mariot & Pigeaud as a theory describing massive mesonic particles ([106], p. 4309).
According to him:
is the 5-dimensional curvature scalar expressible, due to the
cylindricity condition, by quantities in space-time. He claimed to have removed the additional terms which
precluded the derivation of the correct equations of motion. We will briefly present the further dissertation
of R. Vallée below in Section 11.2.1. Huyen Dangvu also studied Jordan–Thiry theory and disagreed with
its interpretation by Mariot & Pigeaud as a theory describing massive mesonic particles ([106], p. 4309).
According to him:
“It seems preferable to us to interpret 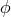 as a scalar field without mass. Jordan–Thiry
theory then will be a unitary theory of three massless fields: a scalar field, a vector field,
and a 2-tensor field of spin 0, 1, 2, respectively.”239
as a scalar field without mass. Jordan–Thiry
theory then will be a unitary theory of three massless fields: a scalar field, a vector field,
and a 2-tensor field of spin 0, 1, 2, respectively.”239
11.1.2 Scalar-tensor theory in the 1960s and beyond
Around Y. Thiry in Paris, the study of his theory continued with J. Hély producing static spherically symmetric solutions of the field equations [253, 252, 251]. They describe a point particle with charge and mass and include the Schwarzschild metric. Due to the different field equations, a direct comparison with the earlier solution by Heckmann et al. of Jordan’s theory (cf. Section 3.1.2) seems not appropriate. However, H. Dangvu also contributed by looking at static and non-static spherically symmetric solutions to the Jordan–Thiry field equations in space-time.240 The solutions carry mass and some of them also electrical charge. Dangvu could compare them with those by Heckmann, Just, and Schücking in the Hamburg group around P. Jordan [108*, 108].
From the full field (particle-) content of Kaluza–Klein theory, mainstream physics became interested most in the scalar field. In spite of the investigations within the framework of the ideas of Kaluza and Klein, and of Jordan’s approach within projective relativity, attention to the scalar field evolved in complete separation from its origin in unitary field theory. Soon, scalar-tensor theories were understood strictly as alternative theories of gravitation. We comment briefly on the loss of this historical perspective the more so as current publications on scalar-tensor theory are more interested in the subsequent modern developments than in the historical record [219, 58]. In the Anglo-Saxon literature, scalar-tensor-theories run under the name of “Brans–Dicke theory”, or, at best, Brans–Dicke–Jordan theory, i.e., two authors being late with regard to Jordan and Thiry are given most of the credit; cf. standard references like ([242], pp. 59, 64, 71, 77, 362); ([438], pp. 1068, 1070, 1098; ([698], pp. 125, 126, 341).241 True, the three groups of successive authors departed from different physical or mathematical ideas; Jordan from a varying gravitational constant as a hypothetical consequence of Dirac’s large number hypothesis, Thiry from a mathematical study of Kaluza–Klein theory and its global aspects, and Brans & Dicke from an implementation of their interpretation of Mach’s principle. A fourth author, W. Scherrer, must be included who was the first of all, and who considered the scalar field as a matter field coupled to gravitation; vid. Section 3.1.2 and [230]. Yet, one should keep in mind that, together with Yang–Mills theories and, perhaps non-local field theory, scalar-tensor theories of gravitation may be also considered as one surviving offspring of unitary field theory. Hence a total loss of historical memory with regard to the origins of scalar-tensor theory appears unjustified.242
11.2 6- and 8-dimensional theories
Since Kaluza had proposed a 5-dimensional space as a framework for a unitary field theory of
the gravitational and electromagnetic fields in 1919, both experimental elementary particle
physics and quantum field theory had progressed. Despite the difficulties with divergencies,
since the mid 1950s renormalization procedures had been stable enough to make quantum field
theory acceptable and needed as a proper formalism for dealing with the known elementary
particles. Nevertheless, in some approaches to unified field theory, it still was thought useful to
investigate classical theory. Thus, in this context theories with new degrees of freedom for the new
fields (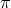 - and
- and 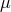 -mesons, neutrino) had to be constructed. We noticed that both in the
Einstein–Schrödinger affine field theory and in the Jordan–Thiry extension of Kaluza’s theory such
attempts had been made. The increase in the dimension of space seemed to be a handy method to
include additional fields. In Section 7.2.2 of Part I, papers of Rumer, Mandel, and Zaycoff
concerning 6-dimensional space have been mentioned. None of them is referred to by the research
described below. It involved theorists working independently in the USA, Great Britain, and
France.
-mesons, neutrino) had to be constructed. We noticed that both in the
Einstein–Schrödinger affine field theory and in the Jordan–Thiry extension of Kaluza’s theory such
attempts had been made. The increase in the dimension of space seemed to be a handy method to
include additional fields. In Section 7.2.2 of Part I, papers of Rumer, Mandel, and Zaycoff
concerning 6-dimensional space have been mentioned. None of them is referred to by the research
described below. It involved theorists working independently in the USA, Great Britain, and
France.
11.2.1 6-dimensional theories
The first of these, B. Hoffmann in Princeton, wanted to describe particles with both electric charge  and magnetic
charge
and magnetic
charge 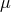 .243
Because the paths of electrically charged particles could be described as geodesics of Kaluza’s 5-dimensional
space, he added another space-dimension. The demand now was that his particles with both kinds of charge
follow geodesics in a 6-dimensional Riemannian (Lorentzian) space
.243
Because the paths of electrically charged particles could be described as geodesics of Kaluza’s 5-dimensional
space, he added another space-dimension. The demand now was that his particles with both kinds of charge
follow geodesics in a 6-dimensional Riemannian (Lorentzian) space 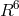 . [277*]. The coordinates in
. [277*]. The coordinates in 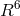 are
denoted here by
are
denoted here by 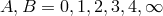 , in
, in 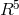 by
by 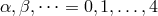 , and in space-time
, and in space-time
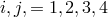 . The metric
. The metric 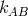 of
of 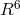 contains, besides the metric
contains, besides the metric 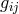 of space-time, two vector
fields
of space-time, two vector
fields 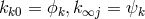 and three scalar fields
and three scalar fields 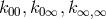 . The scalar fields are disposed of
immediately:
. The scalar fields are disposed of
immediately: 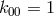 (cylinder condition),
(cylinder condition), 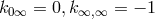 , while
, while 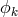 is taken to be the electrical
4-potential:
is taken to be the electrical
4-potential: 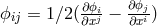 and
and 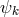 the corresponding quantity following from the dual of the
electrical field tensor
the corresponding quantity following from the dual of the
electrical field tensor 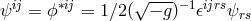 .
.
The geodesic equation 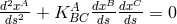 with the Levi-Civita connection
with the Levi-Civita connection 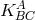 is decomposed
into 3 groups corresponding to
is decomposed
into 3 groups corresponding to 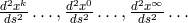 . From the last two equations follows
. From the last two equations follows
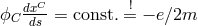 and
and 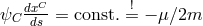 such that the projection of the geodesic
equation of
such that the projection of the geodesic
equation of 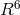 into space-time reads as:
into space-time reads as: 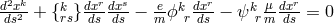 . In order that the
geodesics are timelike curves, the condition
. In order that the
geodesics are timelike curves, the condition 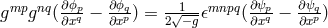 must be fulfilled. It
does as a consequence of the field equations derived from:
must be fulfilled. It
does as a consequence of the field equations derived from:
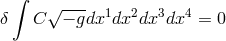
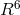 is
is 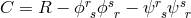 with
with 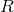 being
the curvature scalar of space-time. With topological questions not asked by him, Hoffmann’s excursion into
6-dimensional space for describing the path of a magnetic monopole was entirely unnecessary. In fact, in his
next paper he applied the method of Einstein and Mayer [175] presented in Section 6.3.2 of
Part I to his particle with electric and magnetic charge and developed a theory in 4 dimensions
[276].
being
the curvature scalar of space-time. With topological questions not asked by him, Hoffmann’s excursion into
6-dimensional space for describing the path of a magnetic monopole was entirely unnecessary. In fact, in his
next paper he applied the method of Einstein and Mayer [175] presented in Section 6.3.2 of
Part I to his particle with electric and magnetic charge and developed a theory in 4 dimensions
[276].
In Manchester, where A. Papapetrou and P. M. S. Blackett worked on possible empirical consequences
of UFT (cf. Section 6.1.2), while L. Rosenfeld wrote about the quantum theory of nuclear forces, a
research fellow Julius Podolanski embarked on a unified field theory in six dimensions [498*]. His motivation came
from Dirac’s equation, more precisely from the algebra of the 15 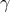 -matrices, interpreted as
representing the algebra of rotations in a 6-dimensional Riemannian space. His manifold
-matrices, interpreted as
representing the algebra of rotations in a 6-dimensional Riemannian space. His manifold 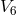 is
decomposed into a flat and geodesic 2-dimensional “sheet” generated by a spacelike and a timelike
translation244,
and a 4-dimensional Lorentz space
is
decomposed into a flat and geodesic 2-dimensional “sheet” generated by a spacelike and a timelike
translation244,
and a 4-dimensional Lorentz space 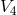 (identified with space-time), both normal to each other. Likewise,
any 6-vector can be decomposed into a part in the 2-sheet and a 4-vector. A material point particle is
assumed to follow a geodesic of
(identified with space-time), both normal to each other. Likewise,
any 6-vector can be decomposed into a part in the 2-sheet and a 4-vector. A material point particle is
assumed to follow a geodesic of 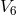 . From the connection of
. From the connection of 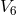 , an induced connection in
, an induced connection in 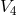 can be
obtained. Invariance with regard to the translations is called “gauge”-invariance in
can be
obtained. Invariance with regard to the translations is called “gauge”-invariance in 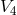 . This means that
gauge-invariant quantities do not depend on the sheet-coordinates. It turned out that the metric of
. This means that
gauge-invariant quantities do not depend on the sheet-coordinates. It turned out that the metric of 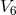 ,
besides leading to the 4-dimensional metric
,
besides leading to the 4-dimensional metric 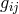 , introduced two skew-symmetric tensors named
fields of constraint. One of them is interpreted as the electromagnetic field. The interpretation
of the second skew field is left open. The scalars in the theory (norms and inner product of
the translations) are assumed constant. The field equations were derived from the curvature
scalar of
, introduced two skew-symmetric tensors named
fields of constraint. One of them is interpreted as the electromagnetic field. The interpretation
of the second skew field is left open. The scalars in the theory (norms and inner product of
the translations) are assumed constant. The field equations were derived from the curvature
scalar of 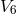 and obviously lead to Einstein’s vacuum field equations in six dimensions; a
matter tensor in
and obviously lead to Einstein’s vacuum field equations in six dimensions; a
matter tensor in 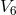 is inserted by hand and restricted to charged pressureless matter. After
a projection into
is inserted by hand and restricted to charged pressureless matter. After
a projection into 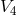 , it turned out that the currents and energy-momentum tensors of the
two skew-symmetric fields had different signs: One field has a positive, the other a negative
energy content. This was not seen as unphysical by the author; he commented: “So it seems
that this theory may contribute to the problem of self-energy”, an allusion to the divergence
problem in quantum field theory ([498*], p. 235), and to the fact that the energy density can
become negative in quantum field theory. But he was disappointed that the 2nd skew field
also had infinite reach: its quanta are massless. He tried to mend this by demanding that a
particle follow a lightlike geodesic in
, it turned out that the currents and energy-momentum tensors of the
two skew-symmetric fields had different signs: One field has a positive, the other a negative
energy content. This was not seen as unphysical by the author; he commented: “So it seems
that this theory may contribute to the problem of self-energy”, an allusion to the divergence
problem in quantum field theory ([498*], p. 235), and to the fact that the energy density can
become negative in quantum field theory. But he was disappointed that the 2nd skew field
also had infinite reach: its quanta are massless. He tried to mend this by demanding that a
particle follow a lightlike geodesic in 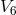 , but did not really succeed. His conclusion was: “A
unitary field theory does not seem possible without introducing quantum theoretical concepts.
This – classical – treatment therefore can only be incomplete” ([498*], p. 258). Pauli noticed
this paper; in the summer term 1953, he had given a course on general relativity including
Kaluza’s 5-dimensional theory. In a letter to Fierz of 3 July 1953 referring to this course we can
read:
, but did not really succeed. His conclusion was: “A
unitary field theory does not seem possible without introducing quantum theoretical concepts.
This – classical – treatment therefore can only be incomplete” ([498*], p. 258). Pauli noticed
this paper; in the summer term 1953, he had given a course on general relativity including
Kaluza’s 5-dimensional theory. In a letter to Fierz of 3 July 1953 referring to this course we can
read:
“In it, also Kaluza’s 5th dimension did occur, and per se it is quite satisfying if now,
in place of it, two additional dimensions with the 3-dimensional rotation group are
introduced (this has already been suggested, if only formalistic, by e.g., Podolanski who
has a 6-dimensional space).” ([491*], p. 186–187.) 245
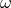 -space consisting
of space-time and an internal sphere-space affixed at any point [468]. From here, a direct line leads to
Pauli’s (unpublished) derivation of the non-Abelian
-space consisting
of space-time and an internal sphere-space affixed at any point [468]. From here, a direct line leads to
Pauli’s (unpublished) derivation of the non-Abelian 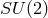 gauge theory presented in letters to Pais. For a
detailed history cf. O’Raifeartaigh’s book ([463], Chapter 7). cf. also the section “A vision of gauge field
theory” in [194], pp. 476–488.
gauge theory presented in letters to Pais. For a
detailed history cf. O’Raifeartaigh’s book ([463], Chapter 7). cf. also the section “A vision of gauge field
theory” in [194], pp. 476–488.
When Josette Renaudie wrote her dissertation with A. Lichnerowicz and M.-A. Tonnelat on
6-dimensional classical unitary field theory in 1956, she also used elementary particles as her motivation
[505, 506*], ([507], p. 3; [508]). However, unlike Podolanski [498] and Yano & Ogane [715], she worked in a
6-dimensional Lorentz space: 2 space-dimensions are added. While Yano & Ogane employed a general
2-parameter isometry group and claimed to have the most general formalism, Renaudie admitted a general
Abelian 2-dimensional isometry group, thus keeping 3 arbitrary scalar functions. Her two Killing vectors
with regard to which the projection from 6-dimensional 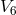 along the trajectories of one Killing vector first
to to
along the trajectories of one Killing vector first
to to 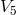 , and then with the 2nd Killing vector to space-time is performed, are spacelike.
Again, an Einstein field equation
, and then with the 2nd Killing vector to space-time is performed, are spacelike.
Again, an Einstein field equation 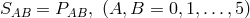 is written down with the
“matter tensor”
is written down with the
“matter tensor” 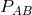 getting its interpretation backwards from the corresponding 4- and
5-dimensional quantities. The Einstein tensor now has 21 independent components and can be
split into a rank 2 symmetric tensor, two 4-vectors and 3 scalar functions. Renaudie gave two
interpretations: (1) these variables stand for a hyperfield composed of gravitational, electromagnetic and
mesonic fields (with the mesonic field a complex vector field), and (2) the field of a particle
of maximal spin 1 in interaction with the gravitational field (p. 68/69). Note that in both
interpretations the scalar fields remain unrelated to physical quantities. The terms in the field equations
describing the interaction of the mesonic and electromagnetic fields are independent of the
geometrical objects in space-time. The Cauchy initial value problem can be set up and solved
properly.246
getting its interpretation backwards from the corresponding 4- and
5-dimensional quantities. The Einstein tensor now has 21 independent components and can be
split into a rank 2 symmetric tensor, two 4-vectors and 3 scalar functions. Renaudie gave two
interpretations: (1) these variables stand for a hyperfield composed of gravitational, electromagnetic and
mesonic fields (with the mesonic field a complex vector field), and (2) the field of a particle
of maximal spin 1 in interaction with the gravitational field (p. 68/69). Note that in both
interpretations the scalar fields remain unrelated to physical quantities. The terms in the field equations
describing the interaction of the mesonic and electromagnetic fields are independent of the
geometrical objects in space-time. The Cauchy initial value problem can be set up and solved
properly.246
Five years later, another thesis advised by A. Lichnerowicz continued the work of J. Renaudie: R. Vallée investigated “The relativistic representation of charged perfect fluids” within 6- and 5-dimensional “space-times” [666*]. According to its title, a focus lies in the material content, a perfect fluid, which also had been briefly dealt with by J. Renaudie ([506], cf. her Section 34). Vallée’s ansatz for the matter tensor in six dimensions is taken over from space-time:
where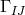 is the metric in 6-dimensional space
is the metric in 6-dimensional space 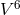 with Lorentz signature,
with Lorentz signature, 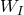 with
with 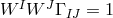 ,
the 6-velocity tangent to the streamlines, and
,
the 6-velocity tangent to the streamlines, and 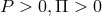 denote “density” and “pressure” ([666],
p. 36). An equation of state
denote “density” and “pressure” ([666],
p. 36). An equation of state 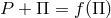 is assumed in order to get the corresponding relation in
space-time. Projection into space-time (metric
is assumed in order to get the corresponding relation in
space-time. Projection into space-time (metric 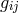 ) via
) via 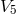 (metric
(metric 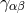 ) led to the matter
tensor of a charged fluid of the form
) led to the matter
tensor of a charged fluid of the form 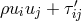 with the electromagnetic energy-momentum
tensor:
with the electromagnetic energy-momentum
tensor: 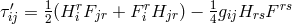 . Electromagnetic field
. Electromagnetic field 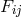 and induction field
and induction field
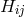 were assumed to be related through
were assumed to be related through 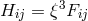 where
where 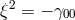 stands for the
additional scalar field in Jordan–Thiry theory. As with Renaudie,
stands for the
additional scalar field in Jordan–Thiry theory. As with Renaudie, 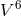 admits a 2-parameter
Abelian group of global isometries. This is research extending the work of Renaudie to further
classes of fluids; it fits to the doctoral theses described in Section 11.1.1 – in essence, they
presented formal developments with restricted relevance to the envisaged physics of unitary field
theory.
admits a 2-parameter
Abelian group of global isometries. This is research extending the work of Renaudie to further
classes of fluids; it fits to the doctoral theses described in Section 11.1.1 – in essence, they
presented formal developments with restricted relevance to the envisaged physics of unitary field
theory.
In 1963, Mariot & Pigeaud again took up the 6-dimensional theory in a
paper247
[388]. After the introduction of a conformal metric in 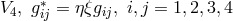 with
with 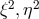 being
the norms squared of the 2 Killing vectors from the additional dimensions, they studied the linear
approximation of the theory with incoherent matter
being
the norms squared of the 2 Killing vectors from the additional dimensions, they studied the linear
approximation of the theory with incoherent matter 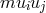 . They were able to identify in
. They were able to identify in 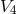 matter
tensors belonging to the electromagnetic field, to a neutral vector meson field and to both a massive neutral
and a charged scalar meson field. Yet, some remaining terms were still not amenable to a physical
interpretation.
matter
tensors belonging to the electromagnetic field, to a neutral vector meson field and to both a massive neutral
and a charged scalar meson field. Yet, some remaining terms were still not amenable to a physical
interpretation.
11.2.2 Eight dimensions and hypercomplex geometry
As early as 1934, an eight-dimensional space with two time-dimensions was introduced in order to describe the gravitational field corresponding to an accelerated electromagnetic field. It then turned out that the two time coordinates were related by the eight geodesic equations such that, essentially, a 7-dimensional Lorentz space remained. Einstein’s vacuum field equations in 8 dimensional space were assumed to hold [421, 422]. In view of the substantial input, the results, reached by approximate calculations only, were meagre: an approximate solution of the gravitational two-body problem; only static electric and constant magnetic fields could be described.
In the 1950s, the idea of using an 8-dimensional space as the stage for UFT seemingly arose by an
extension of the mapping of connections in the same 4-dimensional space to a second copy of such a space.
In Section 2.1.2 we have noted F. Maurer-Tison’s interpretation of (30*): The transport of a
covariant vector 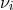 with regard to the connection
with regard to the connection 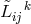 corresponds to the transport of the
contravariant vector
corresponds to the transport of the
contravariant vector 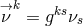 with regard to
with regard to 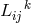 . This situation was turned into a geometry
named semi-metric by Pierre-V. Grosjean in which two identical 4-dimensional spaces (“distinct universes”) were introduced
with the connection
. This situation was turned into a geometry
named semi-metric by Pierre-V. Grosjean in which two identical 4-dimensional spaces (“distinct universes”) were introduced
with the connection 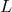 acting in one and its Hermitian conjugated connection
acting in one and its Hermitian conjugated connection 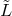 in the
other [235]. Inner products of vectors were allowed only if one vector is in the one space, the
other in the second. His conclusion that the semi-metric geometry would be “the key to the
unitary theory, in the same way as metric geometry was the key to general relativity” is more
than overbearing. All that remains is a (physically empty) mathematical formalism the only
consequence of which was to eventually motivate the scheme of applied mathematics to be discussed
next.
As mentioned in Section 2.6, in close parallel to the complex numbers, a ring formed from
in the
other [235]. Inner products of vectors were allowed only if one vector is in the one space, the
other in the second. His conclusion that the semi-metric geometry would be “the key to the
unitary theory, in the same way as metric geometry was the key to general relativity” is more
than overbearing. All that remains is a (physically empty) mathematical formalism the only
consequence of which was to eventually motivate the scheme of applied mathematics to be discussed
next.
As mentioned in Section 2.6, in close parallel to the complex numbers, a ring formed from 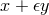 with
real numbers
with
real numbers 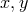 and
and 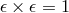 can be introduced: the hypercomplex numbers. Albert
Crumeyrolle built a unitary field theory of the Einstein–Schrödinger type on this number field
[96, 97*, 98, 95]. In a generalization of the formalism noted in Section 10.5.4, he now introduced a
2n-dimensional
can be introduced: the hypercomplex numbers. Albert
Crumeyrolle built a unitary field theory of the Einstein–Schrödinger type on this number field
[96, 97*, 98, 95]. In a generalization of the formalism noted in Section 10.5.4, he now introduced a
2n-dimensional 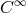 -space
-space 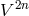 and local charts around points by assigning n hypercomplex numbers
and local charts around points by assigning n hypercomplex numbers
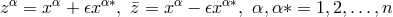 . In another basis,
. In another basis, 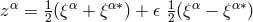 .
The
.
The 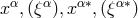 transform among themselves. Again, a “natural adapted reference system” was
introduced in which dual bases derive one from the other by the regular and diagonal
transform among themselves. Again, a “natural adapted reference system” was
introduced in which dual bases derive one from the other by the regular and diagonal 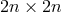 -matrix in
-matrix in
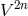 :
:
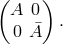
Here, 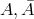 are
are 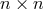 -matrices with
-matrices with 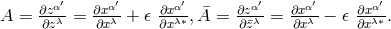 In
In 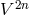 ,
locally a real symmetric covariant tensor could be introduced which decomposes in the coordinate system
,
locally a real symmetric covariant tensor could be introduced which decomposes in the coordinate system
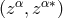 into parts
into parts  . Likewise connections and special unitary connections were defined.
In the end, a system generalizing the weak field equations of UFT resulted. For the physicist, and the more
so for the historian of physics, the paper is a maze of mathematical structures. The author’s statement that
“a new field can be introduced the physical signification of which is not examined here but which could
perhaps have something to do with the hypothesis of an inertial effect of the spin”, remains unfounded
([97], p. 105).
. Likewise connections and special unitary connections were defined.
In the end, a system generalizing the weak field equations of UFT resulted. For the physicist, and the more
so for the historian of physics, the paper is a maze of mathematical structures. The author’s statement that
“a new field can be introduced the physical signification of which is not examined here but which could
perhaps have something to do with the hypothesis of an inertial effect of the spin”, remains unfounded
([97], p. 105).



![Ω = μ√--[∂ (F u ) − ∂ (Fu )] + kμ[∂ (F ϕ ) − ∂ (F ϕ )] i = 0,1,...,3. (430 ) ij ξ i j j i i j j i](article2193x.gif)