9 Einstein II: From 1948 on
In the meantime, Einstein had gone on struggling with his field equations and, in a letter to M. Solovine of 25 November 1948, had become less optimistic ([160*], p. 88):
“Scientifically, I am still lagging because of the same mathematical difficulties which make
it impossible for me to affirm or contradict my more general relativistic field theory […]. I
will not be able to finish it [the work]; it will be forgotten and at a later time arguably must
be re-discovered. It happened this way with so many problems.”115
In his correspondence with Max Born during the second half of the 1940s, Einstein clung to his refusal of the statistical interpretation of quantum mechanics. According to him, physics was to present reality in space and time without, as it appeared to him, ghostly interactions at a distance. In a letter of 3 March 1947, he related this to UFT:
“Indeed, I am not strongly convinced that this can be achieved with the theory of my
continuous field although I have found for it an – until now – apparently reasonable
possibility. Yet the calculatory difficulties are so great that I shall bite the dust until I
myself have found an assured opinion of it. […]” 116
In spite of such reservations, Einstein carried on unflagging with his research. In his next
publication on UFT [148*], he again took a complex (asymmetric) metric field. In order to justify
this choice in comparison to Schrödinger’s who “has based his affine theory […] on real fields
[…]”,117
he presented the following argument: Just by multiplication and the use of a single complex vector 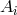 a
Hermitian tensor
a
Hermitian tensor 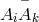 can be constructed. By adding four such terms, the Hermitian metric tensor
can be constructed. By adding four such terms, the Hermitian metric tensor
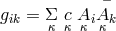 can be obtained. “A non-symmetric real tensor cannot be constructed from vectors in
such close analogy” ([148*], p. 39). Nevertheless, in Einstein’s future papers, the complex metric was
dropped.
can be obtained. “A non-symmetric real tensor cannot be constructed from vectors in
such close analogy” ([148*], p. 39). Nevertheless, in Einstein’s future papers, the complex metric was
dropped.
The field equations were derived from the Lagrangian
i.e., from the Lagrangian (205*) without the multiplier terms. In order to again be able to gain the weak field equations, an additional assumption was made: the skew-symmetric part of the metric (density)![[ik] ˆg](article1139x.gif) be
derived from a tensor “potential”
be
derived from a tensor “potential” 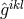 anti-symmetric in all indices. Thus, in the Lagrangian,
anti-symmetric in all indices. Thus, in the Lagrangian, 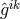 is
replaced by
is
replaced by 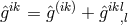 . The motivation behind this trick is to obtain the compatibility equation
(30*) from
. The motivation behind this trick is to obtain the compatibility equation
(30*) from 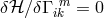 , indirectly. The skew-symmetric part of
, indirectly. The skew-symmetric part of 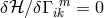 is formed and a
trace taken in order to arrive at
is formed and a
trace taken in order to arrive at ![1 [ik] (ik) s 2ˆg ,l + ˆg Γ [ks] = 0](article1145x.gif) . Introduction of
. Introduction of 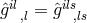 then
shows that
then
shows that 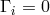 holds. With the help of this equation,
holds. With the help of this equation, 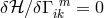 finally reduces to
(30*).
finally reduces to
(30*).
The field equation following directly from independent variation with regard of 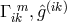 and
and 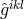 are:
118
are:
118
In addition, the equations hold:
As in [179*], Einstein did not include homothetic curvature into the building of his Lagrangian with the same unconvincing argument: from his (special) field equations and (252*) the vanishing of the homothetic curvature would follow.
In his paper, Einstein related mathematical objects to physical observables such that “the antisymmetric
density 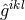 plays the role of an electromagnetic vector potential, the tensor
plays the role of an electromagnetic vector potential, the tensor ![ˆg[ik],l + ˆg[kl],i + ˆg[li],k](article1156x.gif) the role
of current density.” More precisely, the dual object
the role
of current density.” More precisely, the dual object ![s sikl j ∼ 𝜖 (ˆg[ik],l + ˆg[kl],i + ˆg[li],k)](article1157x.gif) with vanishing
divergence
with vanishing
divergence 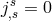 is the (electric) current density ([148*], p. 39).
is the (electric) current density ([148*], p. 39).
Einstein summed up the paper for Pauli on one page or so and concluded: “The great difficulty lies in the
fact that we do not have a method for deriving exact solutions free of singularities, which are the only ones
of physical interest. The few things we were able to calculate strengthened my confidence in this theory.” ([489*],
p. 518)119 In his answer three weeks later, Pauli was soft on “whether a mathematically unified combination of the
electromagnetic and gravitational fields in a classical field theory is possible […]”, but adamant on its
relation to quantum theory:
In his answer three weeks later, Pauli was soft on “whether a mathematically unified combination of the
electromagnetic and gravitational fields in a classical field theory is possible […]”, but adamant on its
relation to quantum theory:
“[…] that I have another opinion than you on the question, mentioned in your letter, of
the physical usability of singularity-free solutions of classical field equations. To me it
deems that, even if such solutions do exist in a suitably chosen field theory, it would
not be possible to relate them with the atomic facts in physics in the way you wish,
namely in a way that avoids the statistical interpretation, in principle.” ([489*], p. 621.)
120
9.1 A period of undecidedness (1949/50)
With two sets of field equations at hand (the “strong” and “weak” versions), it cost some effort for Einstein to decide which of the two was the correct one. As will be seen in Section 9.2, early in 1949 he had found a new way of deriving the “weak” field equations, cf. [149*].121 In a letter of 16 August 1949 to his friend Besso, who had asked him to tell him about his generalized field equations, Einstein presented these “weak” equations and commented:
“Now you will ask me: Did God tell this into your ear? Unfortunately, not. But the way of
proceeding is: identities between the equations must exist such that they are compatible.
[…] For their compatibility, i.e., that continuation from a [time-] slice is possible, there
must be 6 identities. These identities are the means to find the equations. […]” ([163*],
p. 410).122
Six weeks later, on 30 September 1949, Einstein had changed his mind: he now advocated the “strong” version (200*) – (202*) of Section 7.2.
“I recently found a very forceful derivation for this system; it shows that the equations
follow from the generalized field as naturally as the gravitational equations from the
postulate of the symmetric field 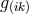 . The examination of the theory still meets with
almost unsurmountable mathematical difficulties […]” ([163*], p. 423).123
. The examination of the theory still meets with
almost unsurmountable mathematical difficulties […]” ([163*], p. 423).123
Consistent with Einstein’s undecidedness are both, his presentation of UFT in Appendix II of the 3rd Princeton edition of The Meaning of Relativity [150*], and another letter to Besso of 15 April 1950 [163*]. In both, he had not yet come to a final conclusion as to which must be preferred, the “weak” or the “strong” equations. To Besso, he explained that the “weak” equations could be derived from a variational principle and thus are “compatible”.
“On the other hand, one is pushed to the stronger system by formal considerations […]. But
the compatibility for this stronger system is problematic; i.e., at first one does not know
whether the manifold of its solutions is sufficiently large. After many errors and efforts I
have succeeded in proving this compatibility” ([163*], p. 439).124
At first, Einstein seems to have followed a strategy of directly counting equations, variables, and
identities. However, early in 1952 he seems to have had a new idea: the 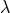 -transformations.
He wrote to Besso on 6 March 1952 that he had made “very decisive progress (a couple of
weeks ago).” The field equations, hitherto not uniquely determined theoretically, now were
known:
-transformations.
He wrote to Besso on 6 March 1952 that he had made “very decisive progress (a couple of
weeks ago).” The field equations, hitherto not uniquely determined theoretically, now were
known:
“ Apart from [coordinate-] transformation invariance, invariance also is assumed for the
transformations of the non-symmetric ‘displacement field’ 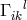 :
: 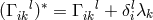 ,
where
,
where 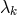 is an arbitrary vector. In this extended group, the old gravitational equations
are no longer covariant […].”([163*], p. 465)125
is an arbitrary vector. In this extended group, the old gravitational equations
are no longer covariant […].”([163*], p. 465)125
We will come back to his final decision in Section 9.2.3.
9.1.1 Birthday celebrations
Einstein’s seventieth birthday was celebrated in Princeton with a seminar on “The Theory of Relativity in Contemporary Science”, in which E. P. Wigner, H. Weyl, and the astronomers G. M. Clemence and H. P. Robertson lectured. UFT was left aside [183]. Weyl, in his lecture “Relativity Theory as a Stimulus in Mathematical Research”, came near to it when he said:
“The temptation is great to mention here some of the endeavors that have been made to utilize these more general geometries for setting up unified field theories encompassing the electromagnetic field beside the gravitational one or even including not only the photons but also the electrons, nucleons, mesons, and whatnot. I shall not succumb to that temptation.” ([693], p. 539.)
As it suited to a former assistant of Einstein, in his article celebrating his master’s 70th birthday, Banesh Hoffmann found friendly if not altogether exuberant words even for Einstein’s struggle with UFT [281*]. For 25 years Einstein had devoted his main scientific work to the problem of the structure of matter and radiation. He tried to gain an insight:
“[…] by abstract reasoning from a few general assumptions. In this he is following the heroic method that proved so successful […] in the theory of relativity. Unfortunately there are many possible approaches, and since each requires a year or more of intensive computation, progress has been heartbreakingly slow.”
That Hoffmann himself was a little outside of mainstream physics can be seen from his remark that quantum theory, now dominating physics, “has developed a stature comparable to that of the theory of relativity.” ([281], p. 54/55.) Hoffmann was also one of the contributors to the special number of Reviews in Modern Physics “in commemoration of the seventieth birthday of Albert Einstein” issued in September 1949. Possibly, the best remembered paper among the 38 articles is Gödel’s “new type of cosmological solutions”, with local rotation and closed timelike world lines, now just named “Gödel’s solution” [227]. Only E. Straus wrote an article about UFT: “Some results in Einstein’s unified field theory” [592*]. The others, big names and lesser known contributors except for the mathematician J. A. Schouten, shunned this topic. Schouten’s contribution surveyed classical meson theories in view of their making contact with the conformal group [539]. In connection with Yukawa’s prediction of a meson and with Hoffmann’s similarity geometry (cf. Section 3.1), he boldly stated: “[…] the conformal field theory failed to ask for a meson field, but the meson field came and asked for a conformal theory!” (ibid., p. 423.) Einstein’s oldest son Hans Albert reported on “Hydrodynamic Forces on a Rough Wall” [180].
Belatedly, toward the end of 1949, some sort of a “Festschrift” for Einstein appeared with 25 contributions of well-known physicists and philosophers, among them six Nobel prize winners [536]. Most interesting is Einstein’s own additional contribution, i.e., his “Autobiographical Notes”, written already in 1946. He described his intentions in going beyond general relativity and essentially presented the content of his paper with E. Straus [179*] containing the “weak field equations” of UFT. His impression was:
“that these equations constitute the most natural generalization of the equations of
gravitation. The proof of their physical usefulness is a tremendously difficult task, inasmuch
as mere approximations will not suffice. The question is: ‘What are the everywhere regular
solutions of these equations?’ ” ([153], p. 93–94.)126
9.2 Einstein 1950
9.2.1 Alternative derivation of the field equations
As we have seen, one of Einstein’s main concerns was to find arguments for choosing a quasi-unique system
of field equations for UFT. His first paper of 1949 opened with a discussion, mostly from the point of view
of mathematics, concerning the possibilities for the construction of UFT with a non-symmetric fundamental
tensor. According to Einstein: “The main difficulty in this attempt lies in the fact that we can build many
more covariant equations from a non-symmetric tensor than from a symmetric one. This is due to the fact
that the symmetric part 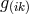 and the antisymmetric part
and the antisymmetric part ![g[ik]](article1169x.gif) are tensors independently” ([149*],
p. 120). As the fundamental tensor is no longer considered symmetrical, the symmetry of the connection (as
in Riemannian geometry) must also be weakened. By help of the conjugate quantities of Section 2.2.2
(Hermitian, transposition symmetry), Einstein’s constructive principle then is to ask “that
conjugates should play equivalent roles in the field-equations.” According to him, this necessitates
the introduction of the particular form (30*) for the compatibility condition. In fact, for the
conjugate:127
are tensors independently” ([149*],
p. 120). As the fundamental tensor is no longer considered symmetrical, the symmetry of the connection (as
in Riemannian geometry) must also be weakened. By help of the conjugate quantities of Section 2.2.2
(Hermitian, transposition symmetry), Einstein’s constructive principle then is to ask “that
conjugates should play equivalent roles in the field-equations.” According to him, this necessitates
the introduction of the particular form (30*) for the compatibility condition. In fact, for the
conjugate:127
In Eq. (257*), two contractions of 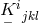 were introduced:
were introduced: 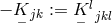 and
and 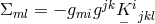 .
Neither
.
Neither 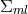 nor
nor 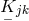 are Hermitian: We have
are Hermitian: We have 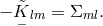 The anti-Hermitian part of
The anti-Hermitian part of 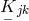 is
given by
is
given by
![s Sk = L [ks] = 0](article1189x.gif) , then
, then 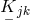 becomes Hermitian, and
becomes Hermitian, and 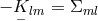 .
Equation (257*) then can be written as
Therefore, Einstein demanded that the contribution of
.
Equation (257*) then can be written as
Therefore, Einstein demanded that the contribution of ![K− [jk]](article1193x.gif) to the Eq. 259*) be in general:
Schrödinger had derived (260*) before by an easier method with the help of the Lie-derivative; cf. [556*]. We
will meet (260*) again in Section 10.3.1. A split of (259*) into symmetric and skew symmetric parts (inside
the bracket) would give the equation:
At best, as a sufficient condition, the vanishing of the symmetric and skew-symmetric parts separately could
take place. Besides (260*) the additional equation would hold:
As we will see, by a further choice (cf. (265*), this equation will be satisfied. Einstein first reformulated
(260*) into:
and then took
as its solution and as part of the field equations. He then added as another field equation:
by which (262*) is satisfied. Thus, in [149*], with a new approach via identities for the curvature
tensor and additional assumptions, Einstein had reached the weak field equations of his previous
paper [148*]. No physical interpretation of the mathematical objects appearing was given by
him.
to the Eq. 259*) be in general:
Schrödinger had derived (260*) before by an easier method with the help of the Lie-derivative; cf. [556*]. We
will meet (260*) again in Section 10.3.1. A split of (259*) into symmetric and skew symmetric parts (inside
the bracket) would give the equation:
At best, as a sufficient condition, the vanishing of the symmetric and skew-symmetric parts separately could
take place. Besides (260*) the additional equation would hold:
As we will see, by a further choice (cf. (265*), this equation will be satisfied. Einstein first reformulated
(260*) into:
and then took
as its solution and as part of the field equations. He then added as another field equation:
by which (262*) is satisfied. Thus, in [149*], with a new approach via identities for the curvature
tensor and additional assumptions, Einstein had reached the weak field equations of his previous
paper [148*]. No physical interpretation of the mathematical objects appearing was given by
him.
9.2.2 A summary for a wider circle
In Appendix II of the third Princeton edition of his book The Meaning of Relativity, Einstein gave an enlarged introduction on 30 pages into previous versions of his UFT. The book was announced with fanfare in the Scientific American [151*]:
“[…] Einstein will set forth what some of his friends say is the long-sought unified field theory. The scientist himself has given no public hint of any such extraordinary development, but he is said to have told close associates at the Institute for Advanced Studies that he regards the new theory as his greatest achievement” ([564], p. 26).
It was Princeton University Press who had used Einstein’s manuscript for this kind of advertising much to his distress; a page of it even “appeared on the front page of The New York Times under the heading ‘New Einstein Theory Gives a Master Key to the Universe’.” ([469*], p. 350.) Einstein’s comment to his friend M. Solovine, on 25 January 1950, was:
“Soon I will also send you the new edition of my little book with the appendix. A few
weeks ago, it has caused a loud rustling noise in the newspaper sheets although nobody
except the translator had really seen the thing. It’s really drole: laurels in advance” ([160*],
p. 96).130
In the book, the translator is identified to have been Sonja Bargmann, the wife of Valentine, who also had translated other essays by Einstein.
In Appendix II, with the assumption that
- all equations remain unchanged with respect to simultaneous substitution of the
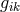 and
and
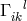 by
by 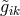 and
and 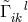 (transposition invariance),
(transposition invariance),
- all contractions of the curvature tensor (54*) vanish,
- that (30*) hold,
Einstein arrived at the field equations131 (30*), (201*), and (202*):
In place of (266*) the equivalent equations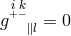 , or
, or 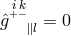 with
with  can be
used. Moreover, if in addition (267*) is taken into account, then also
is satisfied. This is due to a relation to be met again below [(cf. Eq. (276*)]:
([179], Eq. (3.4), p. 733.)
can be
used. Moreover, if in addition (267*) is taken into account, then also
is satisfied. This is due to a relation to be met again below [(cf. Eq. (276*)]:
([179], Eq. (3.4), p. 733.)
For Einstein, this choice (“System I”) “is therefore the natural generalization of the gravitational equation” ([150*], p. 144). A little later in the Appendix he qualified his statement as holding “from a formal mathematical point of view […]” ([150*], p. 150) because the manifold of solutions of “System I” might be too small for physical purposes. Moreover, “System I” could not be derived from a variational principle. He then set up such a variational principle132
with the Hermitian Ricci tensor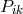 . As Einstein wanted to again get (267*), he introduced another
connection
. As Einstein wanted to again get (267*), he introduced another
connection 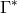 by
by ![Γ k= Γ ∗ k− 2Γ ∗δk ij ij 3 [ij]](article1222x.gif) which does not satisfy
which does not satisfy ![Γ ∗ = Γ ∗ m = 0 j [im ]](article1223x.gif) , such that just
independent components could be varied. The result is his “System Ia”:
with
, such that just
independent components could be varied. The result is his “System Ia”:
with ![[i+l−] ℳi := ˆg ||l](article1225x.gif) . The following identity
holds:133
In order to make vanish
. The following identity
holds:133
In order to make vanish 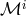 , with the help of a Lagrange multiplier
, with the help of a Lagrange multiplier 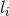 , he introduced the
term
, he introduced the
term ![[ir] li ˆg ,r](article1232x.gif) into the Lagrangian and arrived at ‘System Ib’, i.e., the weak field equations:
In all three systems, equations (249*), (269*), (272*) are to be used for expressing the components of the
(asymmetric) connection by the components of the (asymmetric) metric. The metric then is determined by
the remaining equations for the Ricci tensor.
into the Lagrangian and arrived at ‘System Ib’, i.e., the weak field equations:
In all three systems, equations (249*), (269*), (272*) are to be used for expressing the components of the
(asymmetric) connection by the components of the (asymmetric) metric. The metric then is determined by
the remaining equations for the Ricci tensor.
The only remarks concerning a relationship between mathematical objects and physical observables made by Einstein at the very end of Appendix II are:
- (269*) shows that there is no magnetic current density present (no magnetic monopoles),
- the electric current density (or its dual vector density) is represented by the tensor
![g[ik],l + g[kl],i + g[li],k)](article1234x.gif) .
.
In order to obtain these conclusions, a comparison to Maxwell’s equations has been made (cf. (210*) and (211*)
of Section 7.3). As for all of Einstein’s papers in this class, 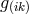 describes the gravito-inertial, and
describes the gravito-inertial, and ![g[ik]](article1236x.gif) the electromagnetic fields.
the electromagnetic fields.
For the first time, Einstein acknowledged that he had seen Schrödinger’s papers without giving a reference, though: “Schrödinger, too, has based his affine theory […]”. Max Born, in his review of Einstein’s book, bluntly stated: “What we have before us might therefore be better described as a program than a theory.” ([41], p. 751.) According to Born, Einstein “tries to find a theory of the classical type of such refined structure that it contains the essential features of atomic and quantum theory as consequences. There are at present few physicists who share this view.” The review by W. H. McCrea reflected his own modesty. Although more cautious, he was very clear:134
“Nevertheless, what has been written here shows how much of the subsequent formulation appears to be entirely arbitrary and how little of it has received physical interpretation. It is clear that a tremendous amount of investigation is required before others than the eminent author himself are enabled to form an opinion of the significance of this work” ([420], p. 129).
The “eminent author” himself confessed in a letter to Max Born of 12 December 1951:
“Unfortunaletly, the examination of the theory is much too difficult for me. After all, a
human being is only a poor wretch!” ([168*], p. 258).135
Also, W. Pauli commented on this 3rd edition. A correspondent who inquired about “the prospects of using Einstein’s new unified field theory as an alternative basis for quantum electrodynamics” obtained a demoralizing answer by him in a letter of 4 July 1950:
“Regarding Einstein’s ‘unified’ field theory I am extremely skeptical. It seems not only arbitrary to add a symmetrical and an anti-symmetrical tensor together but there is also no reason why Einstein’s system of equations should be compatible (the counting of identities between these equations given in the appendix of the new edition turned out to be incorrect). Certainly no work on similar lines will be done in Zürich.” ([490*], p. 137–138)
Einstein’s former assistant and co-author Leopold Infeld sounded quite skeptical as well when he put the focus on equations of motion of charges to follow from “the new Einstein theory”. By referring to the 3rd Princeton edition of The Meaning of Relativity he claimed that, in 1st approximation, “the equations of motion remain Newtonian and are uninfluenced by the electromagnetic field.” But he offered immediate comfort by the possibility “that this negative result is no fault of Einstein’s theory, but of the conventional interpretation by which it was derived” [303].
9.2.3 Compatibility defined more precisely
In a long paragraph (§7) of Appendix II, of this 3rd Princeton edition, Einstein then asked about the definition of what he had termed “compatibility”. This meant that “the manifold of solutions” of the different systems of field equations “is extensive enough to satisfy the requirements of a physical theory” ([150*], p. 150), or put differently, the field equations should not be overdetermined. In view of the “System I”’s containing four more equations, i.e., 84, than the 80 unknowns, this might become a difficulty. Starting from the Cauchy problem, i.e., the time development of a solution off an initial hypersurface, he counted differential equations and the variables to be determined from them.136 To give an example for his method, he first dealt with general relativity and obtained the result that the general solution contains four free functions of three (spacelike) coordinates – “apart from the functions necessary for the determination of the coordinate system” ([150*], p. 155). The corresponding results for “Systems Ia, (I)” according to him turned out to be: 16, (6) arbitrary functions of three variables, respectively. In case “System I” should turn out to be too restrictive to be acceptable as a physical theory, Einstein then would opt for the “weak field equations” (“System Ib”). “However, it must be admitted that in this case the theory would be much less convincing than if system (I) can be preserved” ([150*], p. 160).
This discussion calls back into memory the intensive correspondence Einstein had carried on between
1929 and 1932 with the French mathematician E. Cartan on an equivalent problem within the theory
of teleparallelism, cf. Section 6.4.3 of Part I. At the time, he had asked whether his partial
differential equations (PDEs) had a large enough set of solutions. Cartan had suggested an “index of
generality” 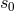 for first-order systems in involution which, essentially, gave the number of arbitrarily
describable free data (functions of 3 spacelike variables) on an initial hypersurface (
for first-order systems in involution which, essentially, gave the number of arbitrarily
describable free data (functions of 3 spacelike variables) on an initial hypersurface (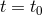 ). He
calculated such indices, for Maxwell’s equations with currents to be
). He
calculated such indices, for Maxwell’s equations with currents to be 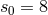 , and without
, and without
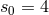 , for Einstein’s vacuum field equations
, for Einstein’s vacuum field equations 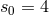 , (in this case 4 free functions of 4 variables
exist137
), and of course, for Einstein’s field equations in teleparallelism theory. Note that Maxwell’s and Einstein’s
vacuum field equations according to Cartan exhibit the same degree of generality. It had taken Cartan a
considerable effort of convincing Einstein of the meaningfulness of his calculations also for physics ([116],
pp. 114, 147, 174). Already in the 3rd Princeton edition of The Meaning of Relativity, in Appendix II [150*],
Einstein tried to get to a conclusion concerning the compatibility of his equations by counting the
independent degrees of freedom but made a mistake. As mentioned above, W. Pauli had noticed this and
combined it with another statement of his rejection of the theory. Compatibility was shown later by
A. Lichnerowicz [369*] (cf. Section 10.5).
, (in this case 4 free functions of 4 variables
exist137
), and of course, for Einstein’s field equations in teleparallelism theory. Note that Maxwell’s and Einstein’s
vacuum field equations according to Cartan exhibit the same degree of generality. It had taken Cartan a
considerable effort of convincing Einstein of the meaningfulness of his calculations also for physics ([116],
pp. 114, 147, 174). Already in the 3rd Princeton edition of The Meaning of Relativity, in Appendix II [150*],
Einstein tried to get to a conclusion concerning the compatibility of his equations by counting the
independent degrees of freedom but made a mistake. As mentioned above, W. Pauli had noticed this and
combined it with another statement of his rejection of the theory. Compatibility was shown later by
A. Lichnerowicz [369*] (cf. Section 10.5).
It is unknown whether Einstein remembered the discussion with Cartan or had heard of
Pauli’s remark, when he tackled the problem once more; in the 4th Princeton edition of his
book The Meaning of Relativity, Appendix II [156*] Cartan’s name is not mentioned. In the
meantime, Mme. Choquet-Bruhat, during her stay at Princeton in 1951 and 1952, had discussed the
Cauch-problem with Einstein such that he might have received a new impulse from her. To
make the newly introduced concept of “strength” of a system of PDE’s more precise, he set
out to count the number of free coefficients of each degree in a Taylor expansion of the field
variables; if all these numbers are non-negative, he called the system of PDE’s “absolutely
compatible”. He then carried out a calculation of the number of coefficients 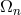 remaining “free for
arbitrary choice” for the free wave equation, Maxwell’s vacuum equations, the Einstein vacuum
equations, and particular field equations of UFT. Let us postpone the details and just list his
results.138
For the wave equation
remaining “free for
arbitrary choice” for the free wave equation, Maxwell’s vacuum equations, the Einstein vacuum
equations, and particular field equations of UFT. Let us postpone the details and just list his
results.138
For the wave equation 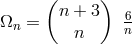 . According to him “the factor
. According to him “the factor 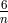 gives the fraction of the
number of coefficients (for the degree
gives the fraction of the
number of coefficients (for the degree 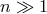 ), which remain undetermined by the differential equation”
([156*], p. 152). Similarly, he found for the Maxwell vacuum equations,
), which remain undetermined by the differential equation”
([156*], p. 152). Similarly, he found for the Maxwell vacuum equations, 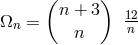 . Einstein noted
that by introducing the vector potential
. Einstein noted
that by introducing the vector potential 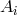 , and taking into account the Lorentz gauge, i.e., by dealing
with
, and taking into account the Lorentz gauge, i.e., by dealing
with
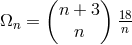 . He ascribed the increase in the number of freely selectable
coefficients (loss of strength) to the gauge freedom for the vector potential. For the Einstein
vacuum equations, he obtained
. He ascribed the increase in the number of freely selectable
coefficients (loss of strength) to the gauge freedom for the vector potential. For the Einstein
vacuum equations, he obtained 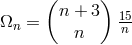 . In applying his method to the “weak” field
equations of Section 9.2.2, Einstein arrived at
. In applying his method to the “weak” field
equations of Section 9.2.2, Einstein arrived at 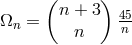 . In comparing this to the
calculation for other field equations in UFT, he concluded that “the natural generalization
of the gravitational equations in empty space” is given by the “weak” field equations ([156*],
p. 164).
. In comparing this to the
calculation for other field equations in UFT, he concluded that “the natural generalization
of the gravitational equations in empty space” is given by the “weak” field equations ([156*],
p. 164).
Obviously, Einstein was not satisfied by his calculations concerning the “strength” of
PDE’s. In the 5th Princeton edition of his book The Meaning of Relativity, Appendix II
[158*],139
he again defined a system of PDE’s as “absolutely compatible” if, in a Taylor expansion of the field variable
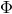 , the number of free
, the number of free 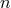 -th order coefficients
-th order coefficients 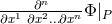 , at a point
, at a point 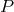 does not become
negative. He then gave a name to the number of free coefficients calculated before: he called it
“coefficient of freedom”. The larger this coefficient is, the less acceptable to him is the system of
PDE’s. Let
does not become
negative. He then gave a name to the number of free coefficients calculated before: he called it
“coefficient of freedom”. The larger this coefficient is, the less acceptable to him is the system of
PDE’s. Let 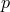 denote the number of field variables,
denote the number of field variables,  the number of field equations of order
the number of field equations of order
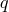 , and
, and 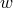 the number of identities among the field equations in the form of PDE’s of order
the number of identities among the field equations in the form of PDE’s of order
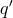 . Then, writing
. Then, writing  in place of the previous
in place of the previous 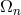 , his formulas could be condensed into:
, his formulas could be condensed into:
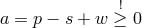 required for absolute compatibility;
required for absolute compatibility; 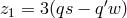 is the “coefficient of
freedom.”140
Again, Einstein calculated
is the “coefficient of
freedom.”140
Again, Einstein calculated 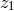 for several examples, among them Maxwell’s vacuum field equations in flat
space-time:
with the identities
Here
for several examples, among them Maxwell’s vacuum field equations in flat
space-time:
with the identities
Here 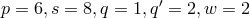 . In agreement with the result from the previous edition, the
calculation led him to
. In agreement with the result from the previous edition, the
calculation led him to 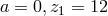 . In contrast, it turned out that the “coefficient of freedom” for the
gravitational vacuum field equations in general relativity, in the 2nd calculation became smaller, i.e.,
. In contrast, it turned out that the “coefficient of freedom” for the
gravitational vacuum field equations in general relativity, in the 2nd calculation became smaller, i.e.,
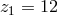 ([158*], p. 139). Fortunately, now both equations have the same “index of generality” (Cartan)
and the same “coefficient of freedom” (Einstein). Likewise, Einstein found
([158*], p. 139). Fortunately, now both equations have the same “index of generality” (Cartan)
and the same “coefficient of freedom” (Einstein). Likewise, Einstein found 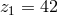 instead of the previous
instead of the previous
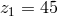 for the “weak”, and
for the “weak”, and 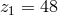 for a concurring system with transposition invariance such that he
again adopted the “weak” one as before. (280*) with its values for
for a concurring system with transposition invariance such that he
again adopted the “weak” one as before. (280*) with its values for 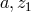 is not yet the correct
formula. Such a formula was derived for involutive, quasi-linear systems of PDEs by a group of
relativists around F. Hehl at the University of Cologne at the end of the 1980s ([595*], Eqs. (2.9),
(2.10), [596]). By their work, also the relation between the Cartan coefficient of generality and
Einstein’s coefficient of freedom has now been provided. According to M. Sué ([595], p. 398), it
seems that Einstein’s coefficient of freedom is better suited for a comparison of the systems
investigated than Cartan’s degré d’arbitraire. In mathematics, a whole subdiscipline has evolved
dealing with the Cartan–Kähler theorem and the Cartan-Characters for systems of PDE’s.
Cf. [57].
is not yet the correct
formula. Such a formula was derived for involutive, quasi-linear systems of PDEs by a group of
relativists around F. Hehl at the University of Cologne at the end of the 1980s ([595*], Eqs. (2.9),
(2.10), [596]). By their work, also the relation between the Cartan coefficient of generality and
Einstein’s coefficient of freedom has now been provided. According to M. Sué ([595], p. 398), it
seems that Einstein’s coefficient of freedom is better suited for a comparison of the systems
investigated than Cartan’s degré d’arbitraire. In mathematics, a whole subdiscipline has evolved
dealing with the Cartan–Kähler theorem and the Cartan-Characters for systems of PDE’s.
Cf. [57].
The fact that Einstein had to correct himself in his calculations of the “coefficient of freedom” already may raise a feeling that there exists a considerable leeway in re-defining field variables, number and order of equations etc. Moreover, he did not prove the independence of the relative order of “strength” for two PDE’s from mathematical manipulations affecting the form of the equations but not their physical content: remember (279*), (282*), (283*). Regrettably, it is to be noted that Einstein’s last attempt to gain a reliable mathematical criterion for singling out one among the many possible choices for the field equations in UFT remained unconvincing.141
9.2.4 An account for a general public
Following an invitation by the editors of Scientific American to report on his recent research, Einstein made it clear that he would not give
“[…] a detailed account of it before a group of readers interested in science. That should be done only with theories which have been adequately confirmed by experiment.” ([152*], p. 14.) 142
He then talked about the epistemological basis of science, men’s curiosity and passion for the
understanding of nature before touching upon problems connected with a generalization of general
relativity. Two questions were very important, though not yet fully answered: the uniqueness of the field
equations and their “compatibility”. He then sketched the three systems of field equations obtained, here
denoted 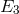 (System I), and
(System I), and 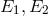 (Systems Ia, Ib). He again stressed that
(Systems Ia, Ib). He again stressed that 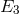 (System I) “is the
only really natural generalization of the equations of gravitation”. However, it was not a compatible system
as were the other two.
(System I) “is the
only really natural generalization of the equations of gravitation”. However, it was not a compatible system
as were the other two.
“The skeptic will say: ‘It may well be true that this system of equations is reasonable from a logical standpoint. But this does not prove that it corresponds to nature.’ You are right, dear skeptic. Experience alone can decide the truth. Yet we have achieved something if we have succeeded in formulating a meaningful and precise question.” ([152*], p. 17.)
Painstaking efforts and probably new mathematics would be required before the theory could be confronted with experiment. The article is illustrated by a drawing of Einstein’s head by the American artist Ben Shahn ([152], p. 17).
There were not only skeptics but people like Dr. C. P. Johnson in the Chemistry Department of
Harvard University who outrightly criticized “Dr. Albert Einstein’s recent unified field theory” [311]. He
pointed out that the theory permits a class of similarity solutions, i.e., with 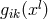 also
also 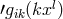 solves
the field equations. For a system of two charged and one uncharged massive bodies he qualitatively
constructed a contradiction with Coulomb’s law. Einstein replied with a letter printed right after Johnson’s
by stating that if solutions depending upon a continuous parameter exist, “then the field equations must
prevent the coexistence within one system of such elementary solutions pertaining to arbitrary values
of their parameters.” The underlying reason was that “for a system of field equations to be
acceptable from a physical point of view, it has to account for the atomic structure of reality.”
This would entail that regions of space corresponding to a ‘particle’ have discrete masses and
charges. The coexistence of similar solutions “in one and the same world” would make the
theory unacceptable [161]. As we shall see, the situation of Einstein’s UFT was worse: it did not
lead to Coulomb’s law – at least not in the lowest approximations. See Sections 9.3.3, 9.6, and
Section 10.3.2.
solves
the field equations. For a system of two charged and one uncharged massive bodies he qualitatively
constructed a contradiction with Coulomb’s law. Einstein replied with a letter printed right after Johnson’s
by stating that if solutions depending upon a continuous parameter exist, “then the field equations must
prevent the coexistence within one system of such elementary solutions pertaining to arbitrary values
of their parameters.” The underlying reason was that “for a system of field equations to be
acceptable from a physical point of view, it has to account for the atomic structure of reality.”
This would entail that regions of space corresponding to a ‘particle’ have discrete masses and
charges. The coexistence of similar solutions “in one and the same world” would make the
theory unacceptable [161]. As we shall see, the situation of Einstein’s UFT was worse: it did not
lead to Coulomb’s law – at least not in the lowest approximations. See Sections 9.3.3, 9.6, and
Section 10.3.2.
Nevertheless, Einstein remained optimistic; in the same letter to Max Born, in which he had admitted his shortcoming vis-a-vis the complexity of his theory, he wrote:
“At long last, the generalization of gravitation from a formal point of view now is fully
convincing and unambiguous – unless the Lord has chosen a totally different way which no
one can imagine.”143
His Italian colleague Bruno Finzi was convinced that the final aim had been reached:
“[…] all physical laws laws of the macrocosm reduce to two geometrical identities […].
Therefore, the game is over, and the geometric model of the macrocosm has been constructed.”([200],
p. 83)144
However, at the end of his article, Finzi pointed out that it might be difficult to experimentally verify the theory, and thought it necessary to warn that even if such an empirical base had been established, this theory would have to be abandoned after new effects not covered by it were observed.
9.3 Einstein 1953
In the fourth edition of Einstein’s The Meaning of Relativity, invariance with regard to 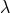 -transformations
was introduced as a new symmetry principle (cf. (52*) of Section 2.2.3). Also transposition invariance is now
claimed to be connected to the “indifference of the theory” (UFT) with respect “to the sign of
electricity” ([156*], p. 144). This interpretation rests on Einstein’s identification of the electric
current density with
-transformations
was introduced as a new symmetry principle (cf. (52*) of Section 2.2.3). Also transposition invariance is now
claimed to be connected to the “indifference of the theory” (UFT) with respect “to the sign of
electricity” ([156*], p. 144). This interpretation rests on Einstein’s identification of the electric
current density with ![g + g + g [ik],l [kl],i [li],k](article1290x.gif) . Einstein still grappled with the problem of how to
set up a convincing system of field equations. As in the previous edition, he included (269*)
as an “a priori condition” in his variational principle by help of a (1-form)-multiplier
. Einstein still grappled with the problem of how to
set up a convincing system of field equations. As in the previous edition, he included (269*)
as an “a priori condition” in his variational principle by help of a (1-form)-multiplier 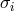 .
However, he renounced using
.
However, he renounced using 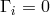 . Without specification of the Lagrangian
. Without specification of the Lagrangian 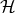 , from
, from
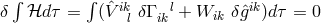 the field equations follow – without use of the multiplier-term –
to be:
the field equations follow – without use of the multiplier-term –
to be:
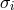 led to the equations (named “System II” by Einstein)
A paragraph then was devoted to the choice of the proper Lagrangian. Einstein started from (196*) and
removed a divergence term in
led to the equations (named “System II” by Einstein)
A paragraph then was devoted to the choice of the proper Lagrangian. Einstein started from (196*) and
removed a divergence term in 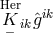 . After variation (with inclusion of the multiplier term) the ensuing
field equations, Einstein’s “system IIa”, were:
i.e., a version of the Einstein–Straus weak field equations. The road to the weak field equations (287*) – (290*)
followed here still did not satisfy Einstein, because in it the skew-symmetric parts of both the metric and
the connection could also be taken to be purely imaginary. In order to exclude this possibility and work
with a real connection, he introduced
. After variation (with inclusion of the multiplier term) the ensuing
field equations, Einstein’s “system IIa”, were:
i.e., a version of the Einstein–Straus weak field equations. The road to the weak field equations (287*) – (290*)
followed here still did not satisfy Einstein, because in it the skew-symmetric parts of both the metric and
the connection could also be taken to be purely imaginary. In order to exclude this possibility and work
with a real connection, he introduced 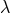 -transformations and presented a further derivation of the field
equations. He set up a variational principle invariant under the
-transformations and presented a further derivation of the field
equations. He set up a variational principle invariant under the 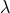 -transformation and arrived at the same
system of field equations as before. The prize payed is the exclusion of a physical interpretation of the
torsion tensor.
-transformation and arrived at the same
system of field equations as before. The prize payed is the exclusion of a physical interpretation of the
torsion tensor.
In a discussion covering twelve pages, Einstein again took up the question of “compatibility” from the previous edition and introduced the concept of the “strength” of a system of differential equations in order to bolster up his choice of field equation. A new principle applying to physical theories in general is put forward: “The system of equations is to be chosen so that the field quantities are determined as strongly as possible” ([156*], p. 149). In Section 9.2.3, a detailed discussion of this new principle has been given such that we need not dwell on it. The paucity of physical input into Einstein’s approach to UFT becomes obvious here. May it suffice to say that according to the new principle the weak field equations (277*), (278*) are called “stronger” than the strong field equations (268*). However, this has lead to the misleading labeling of the system II as the “strong system” [704*]. The relation of geometrical objects to physical observables remained unchanged when compared to the 3rd edition ([150*]). Einstein saw a close relationship to Maxwell’s theory only in the linear approximation where “the system decomposes into two sets of equations, one for the symmetric components of the field, and the other for the antisymmetric components.[…] In the rigorous theory this independence no longer holds.” ([156*], p. 147.)
Both, the concept of “strength” of a system of differential equations and the concluding §5 “General remarks concerning the concepts and methods of theoretical physics” point to Einstein’s rather defensive position, possibly because of his feeling that the particular field equations of unified field theory for which he strove so hard, rested on flexible ground. This was due not only to the arbitrariness in picking a particular field equation from the many possibilities, but also to the failure of the theory to include a description of concepts forming an alternative to quantum theory. Einstein stuck to the classical field and rejected both de Broglie’s “onde pilote”, and Bohm’s attempt away from the statistical interpretation of the wave function. At the very end of his Meaning of Relativity he explained himself in this way:
“[…] I see in the present situation no possible way other than a pure field theory, which then however has before it the gigantic task of deriving the atomic character of energy. […] We are […] separated by an as yet insurmountable barrier from the possibility of confronting the theory with experiment. Nevertheless, I consider it unjustified to assert, a priori, that such a theory is unable to cope with the atomic character of energy.” ([156*], p. 165.)
An indirect answer to this opinion was given by F. J. Dyson in an article on “field theory” in the Scientific American. He claimed “that there is an official and generally accepted theory of elementary particles, known as the ‘quantum field theory’.” According to him, while there still was disagreement about the finer details of the theory and its applications:
“The minority who reject the theory, although led by the great names of Albert Einstein and P. A. M. Dirac, do not yet have any workable alternative to put in its place.” ([137], p. 57.)
Such kind of sober judgment did not bother The New York Times which carried an almost predictable headline: “Einstein Offers New Theory to Unify Law of the Cosmos.” ([469], p. 350.)
Privately, in a letter to M. Solovine of 28 May 1953, Einstein seemed less assured. Referring to the
appendix of this 4th edition of “The Meaning of Relativity”, he said: “[…] Of course, it is the
attempt at a theory of the total field; but I did not wish to give the thing such a demanding
name. Because I do not know, whether there is physical truth in it. From the viewpoint of a
deductive theory, it may be perfect (economy of independent concepts and hypotheses).” ([160*],
p. 96).145
9.3.1 Joint publications with B. Kaufman
In the Festschrift for Louis de Broglie on the occasion of his 60th birthday (15.8.1952) organized by
M.-A. Tonnelat and A. George, Einstein again summarized his approach to UFT, now in an article with his
assistant Bruria Kaufman [172*]. In a separate note, as kind of a
preface he presented his views on quantum theory, i.e., why he still was trying “[…] to solve
the quantum riddle on another path or, to at least help for preparing such a solution.” ([155*],
p. 4.)146 He expressed his well-known epistemological position that something like a “real state” of a physical system
exists objectively, independent of any observation or measurement. A list of objections to the
majority interpretation of quantum theory was given. At the end of the note, a link to UFT was
provided:
He expressed his well-known epistemological position that something like a “real state” of a physical system
exists objectively, independent of any observation or measurement. A list of objections to the
majority interpretation of quantum theory was given. At the end of the note, a link to UFT was
provided:
“My endeavours to complete general relativity by a generalization of the gravitational
equations owe their origin partially to the following conjecture: A reasonable general
relativistic field theory could perhaps provide the key to a more perfect quantum theory.
This is a modest hope, but in no way a creed.” ([155], p. 14.)147
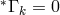 holds which leads to simplifications. Under a
holds which leads to simplifications. Under a
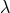 -transformation the Ricci curvature is not invariant [cf. (87*)]. In order to make the variational principle
invariant, due to
-transformation the Ricci curvature is not invariant [cf. (87*)]. In order to make the variational principle
invariant, due to
![∫ ∫ ∫ [il] δ d4x ˆgikK ik(Γ ) = δ[ d4x ˆgikK ik(∗Γ ) + 2 d4x ˆg ,lλi ] − −](article1306x.gif) , as an ad-hoc- (or as Einstein & Kaufman
called it, an a priori-) condition is needed:
The further derivation of the field equations led to the known form of the weak field equations:
, as an ad-hoc- (or as Einstein & Kaufman
called it, an a priori-) condition is needed:
The further derivation of the field equations led to the known form of the weak field equations:
Here, the covariant derivative refers to the connection 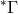 and
and 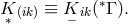
In addition, a detailed argument was advanced for ruling out the strong field equations. It rests
partially on their failure to guarantee the possibility to superpose weak fields. The method used
is a weak-field expansion of the metric and the affine connection in a small parameter  :
:

In an appendix to the paper with title “Extension of the Relativistic Group” [172*], Einstein combined
the “group” of coordinate transformations with the 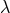 -transformations to form a larger transformation
group
-transformations to form a larger transformation
group 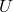 . (cf. the letter to Besso mentioned in Section 9.1.) He then discussed the occurring geometric
objects as representations of this larger group and concluded: “The importance of the extension of the
transformation group to
. (cf. the letter to Besso mentioned in Section 9.1.) He then discussed the occurring geometric
objects as representations of this larger group and concluded: “The importance of the extension of the
transformation group to 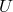 consists in a practically unique determination of the field equation.”([172*],
p. 341.)149
consists in a practically unique determination of the field equation.”([172*],
p. 341.)149
The next paper with Bruria Kaufman may be described as applied mathematics [173*]. Einstein returned
to the problem, already attacked in the paper with E. Straus, of solving (30*) for the connection in terms of
the metric and its derivatives. The authors first addressed the question: “What are necessary and sufficient
conditions for constant signature of the asymmetric metric-field to hold everywhere in space-time?” At first,
it was to be shown “that the symmetric part 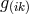 of the tensor
of the tensor 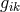 is a Riemannian metric with
constant signature”. For a proof, the conditions
is a Riemannian metric with
constant signature”. For a proof, the conditions 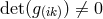 and a further algebraic inequality were
needed. In addition, the connection
and a further algebraic inequality were
needed. In addition, the connection 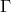 , calculated from
, calculated from 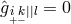 , had to be finite at any point
and “algebraically determined”. This is meant in the sense of interpreting
, had to be finite at any point
and “algebraically determined”. This is meant in the sense of interpreting 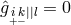 as an
inhomogeneous linear equation for the components of
as an
inhomogeneous linear equation for the components of 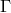 . The situation was complicated by the
existence of the algebraic invariants of the non-symmetric
. The situation was complicated by the
existence of the algebraic invariants of the non-symmetric 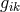 as well as by the difficulty
to solve for the connection as a functional of the metric tensor. Although not necessary for
a solution of the field equations, according to the authors it is “of interest to give a closed
expression for the
as well as by the difficulty
to solve for the connection as a functional of the metric tensor. Although not necessary for
a solution of the field equations, according to the authors it is “of interest to give a closed
expression for the 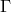 as a function of the
as a function of the 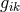 and its first derivatives.” This problem had
been addressed before and partial results achieved by V. Hlavatý [258, 260*], and S. N. Bose
[52*].150
The papers by M.-A. Tonnelat published earlier and presenting a solution were not referred to at all
[622*, 623*, 630*, 629*].
and its first derivatives.” This problem had
been addressed before and partial results achieved by V. Hlavatý [258, 260*], and S. N. Bose
[52*].150
The papers by M.-A. Tonnelat published earlier and presenting a solution were not referred to at all
[622*, 623*, 630*, 629*].
In the sequel, 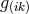 is given a Lorentz signature. By using special coordinates in which
is given a Lorentz signature. By using special coordinates in which 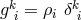 (no summation on the index i), it can be seen that “
(no summation on the index i), it can be seen that “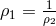 is on the unit circle from which the point
is on the unit circle from which the point
 has been excluded”; the other two roots
has been excluded”; the other two roots 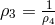 are positive. It is shown in the paper that
among the three algebraic invariants to be built from
are positive. It is shown in the paper that
among the three algebraic invariants to be built from 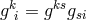 only two are independent:
only two are independent:
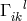 ” the authors derive
([173*], p. 237):
In a lengthy calculation filling six pages, a formal solution to the compatibility equation (30*), seen as an
algebraic equation for
” the authors derive
([173*], p. 237):
In a lengthy calculation filling six pages, a formal solution to the compatibility equation (30*), seen as an
algebraic equation for 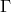 is then presented: “[…] it is cumbersome, and not of any practical utility for
solving the differential equations” ([173], p. 238).
is then presented: “[…] it is cumbersome, and not of any practical utility for
solving the differential equations” ([173], p. 238).
9.3.2 Einstein’s 74th birthday (1953)
Einstein agreed to let his 74th birthday be celebrated with a fund-raising event for the establishing of the Albert Einstein College of Medicine of Yeshiva University, New York. Roughly two weeks later, according to A. Pais The New York Times carried an article about Einstein’s unified field theory on the front page [471]. It announced the appearance of the 4th Princeton edition of The Meaning of Relativity with its Appendix II, and reported Einstein as having stated that the previous version of 1950 of the theory had still contained one important difficulty. According to him: “[…] This last problem of the theory now finally has been solved in the past months.”151 Probably, this refers to Einstein’s new way of calculating his “coefficient of freedom” introduced for mirroring the “strength” of partial differential equations. In a letter to Carl Seelig of 14 September 1953, Einstein tried to explain the differences between the 3rd and the 4th edition of The Meaning of Relativity:
“A new theory often only gradually assumes a stable, definite form when later findings
allow the making of a specific choice among the possibilities given a priori. This development
is closed now in the sense that the form of the field laws is completely fixed. – The
theory’s mathematical consistence cannot be denied. Yet, the question about its physical
foundation still is completely unsettled. This follows from the fact that comparison with
experience is bound to the discovery of exact solutions of the field equations which seems
impossible at the time being.”152 ([570], p. 401–402)
([570], p. 401–402)
9.3.3 Critical views: variant field equation
Already in 1950, Infeld had pointed to the fact that the equations of motion for particles following from Einstein’s UFT (weak field equations), calculated in the same way as in general relativity, did not lead to the Lorentz equations of motion [304*]. This result was confirmed by Callaway in 1953. Callaway identified the skew part of the fundamental tensor with the electromagnetic field and applied a quasistatic approximation built after the methods of Einstein and Infeld for deriving equations of motion for point singularities. He started from Einstein’s weak field equations and showed that (208*) could not influence the equations of motion. His conclusion was that he could reduce “Einstein’s new unified field theory to something like Maxwell’s equations in a sufficiently low approximation”, but could not obtain the Lorentz equation for charged particles treated as singularities in an electromagnetic field [69*].
In order to mend this defect, Kursunŏglu modified the Einstein–Straus weak field equations by beginning with
the identity (257*) and adding another identity formed from the the metric 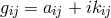 and its 1st derivatives only
[342, 343*]:153
and its 1st derivatives only
[342, 343*]:153
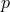 real or imaginary, and154
where
real or imaginary, and154
where 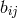 is the inverse of
is the inverse of 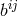 .
. ![Iikl := k[ik],l + k[kl],i + k [li],k](article1346x.gif) is connected with the electrical 4-current
density
is connected with the electrical 4-current
density 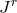 through
through 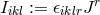 .
.
In fact, as Bonnor then showed in the lowest approximation (linear in the gravitational,
quadratic in the electromagnetic field), the static spherically symmetric solution contains only
two arbitrary constants 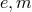 besides
besides  which can be identified with elementary charge
and mass; they are separately selectable [33*]. However, in place of the charge appearing in the
solutions of the Einstein–Maxwell theory, now for
which can be identified with elementary charge
and mass; they are separately selectable [33*]. However, in place of the charge appearing in the
solutions of the Einstein–Maxwell theory, now for 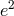 the expression
the expression 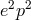 , and for
, and for 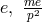 occurred in the same solution. The definition of mass seemed to be open, now. For vanishing
electromagnetic field, the solution reduced to the solution for the gravitational field of general
relativity.
occurred in the same solution. The definition of mass seemed to be open, now. For vanishing
electromagnetic field, the solution reduced to the solution for the gravitational field of general
relativity.
In a discussion concerning the relation of matter and geometry, viz. matter as a “source” of geometry or as an intrinsic part of it, exemplified by the question of the validity of Mach’s principle, J. Callaway tried to mediate between the point of view of A. Einstein with his unified field theory already incorporating matter, geometrically, and the standpoint of J. A. Wheeler who hoped for additional relations between matter and space-time fixing the matter tensor as in the case of the Einstein–Maxwell theory ([70*], p. 779). Callaway concluded that “if the approach of field theory is accepted, it is necessary to construct a theory in which space-time and matter enter as equals.” But he would not accept UFT as an alternative to quantum theory.
9.4 Einstein 1954/55
The last paper with B. Kaufman was submitted three months before, and appeared three months after
Einstein’s death [174*]. In it, the authors followed yet two other methods for deriving the field equations of
UFT. Although the demand for transposition-invariance was to play a considerable role in the setting up of
the theory, in the end invariance under 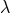 -transformations became the crucial factor. In the first approach
(§1), instead of the previously used connection
-transformations became the crucial factor. In the first approach
(§1), instead of the previously used connection 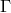 , Einstein and Kaufman introduced another one,
, Einstein and Kaufman introduced another one, 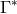 ,
containing four new variables (a 1-form)
,
containing four new variables (a 1-form) 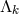 “supernumerary to the description of the field”, and defined
by:
“supernumerary to the description of the field”, and defined
by:
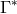 and
and 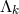 were treated as independent variables; after the
variation
were treated as independent variables; after the
variation 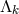 could be fixed arbitrarily (“normed”). This trick allowed that four variational field equations
could replace four equations put in by hand as had been the equation
could be fixed arbitrarily (“normed”). This trick allowed that four variational field equations
could replace four equations put in by hand as had been the equation 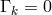 in earlier approaches. The
following relation resulted:
such that the Lagrangian could be written as
After the variation with respect to
in earlier approaches. The
following relation resulted:
such that the Lagrangian could be written as
After the variation with respect to 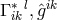 , and
, and 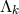 the choice
the choice 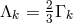 was made leading to
was made leading to
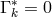 . Although the wanted transposition-invariant field equations did come out, the authors were
unhappy about the trick introduced. “The reason for our difficulties is that we require the field
equations to be transposition-invariant, but we start out from a variational function which
does not have that property. The question arises naturally whether we cannot find a form of
the variational function which will itself be transposition-invariant, […].” ([174*], p. 131.) In
order to obtain such a Lagrangian, they replaced the connection by a quantity
. Although the wanted transposition-invariant field equations did come out, the authors were
unhappy about the trick introduced. “The reason for our difficulties is that we require the field
equations to be transposition-invariant, but we start out from a variational function which
does not have that property. The question arises naturally whether we cannot find a form of
the variational function which will itself be transposition-invariant, […].” ([174*], p. 131.) In
order to obtain such a Lagrangian, they replaced the connection by a quantity 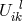 called
“pseudo-tensor”. It is transforming like a tensor only under linear coordinate transformations (§2 – §3):
From (307*) we see that
called
“pseudo-tensor”. It is transforming like a tensor only under linear coordinate transformations (§2 – §3):
From (307*) we see that 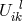 does not transform like a connection. As a function of
does not transform like a connection. As a function of 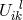 the Ricci tensor:
is transposition-invariant, i.e.,
the Ricci tensor:
is transposition-invariant, i.e., 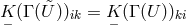 . With regard to a
. With regard to a 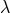 -transformation (52*) the
“pseudo-tensor”
-transformation (52*) the
“pseudo-tensor” 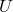 transforms as:
A short calculation shows that
transforms as:
A short calculation shows that 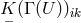 is invariant under (52*).
is invariant under (52*).
As a Lagrangian, now 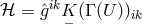 was taken. Variation with respect to the variables
was taken. Variation with respect to the variables 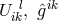 , i.e.,
, i.e.,
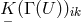 given by (308*). Although the authors do not say it, Eqs. (311*) and (312*) are
equivalent to the “weak” field equations (287*) – (290*). By inserting infinitesimal coordinate- and
given by (308*). Although the authors do not say it, Eqs. (311*) and (312*) are
equivalent to the “weak” field equations (287*) – (290*). By inserting infinitesimal coordinate- and
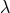 -transformations into (310*), five identities called “Bianchi-identities” result. Modulo the field equations,
holds as well. With the help of special infinitesimal coordinate transformations and the Bianchi-identities a
“conservation law for energy and momentum” is derived:
where
-transformations into (310*), five identities called “Bianchi-identities” result. Modulo the field equations,
holds as well. With the help of special infinitesimal coordinate transformations and the Bianchi-identities a
“conservation law for energy and momentum” is derived:
where 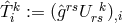 .
.
The results of this paper [174*] were entered into the 5th Princeton edition of The Meaning of Relativity, Appendix II [158*].155 In “A note on the fifth edition” dated December 1954, Einstein wrote:
“For I have succeeded – in part in collaboration with my assistant B. Kaufman – in simplifying the derivations as well as the form of the field equations. The whole theory becomes thereby more transparent, without changing its content” ([158*], page before p. 1).156
From a letter to his friend Solovine in Paris of 27 February 1955, we note that Einstein
was glad: “At least, yet another significant improvement of the general theory of the
gravitational field (non-symmetric field theory) has been found. However, the thus simplified
equations also cannot be examined by the facts because of mathematical difficulties”. ([160*],
p. 138)157 In this edition of The Meaning of Relativity’, he made a “remark on the physical interpretation”. It
amounted to assign
In this edition of The Meaning of Relativity’, he made a “remark on the physical interpretation”. It
amounted to assign ![ˆg[is,s]](article1388x.gif) to the (vanishing) magnetic current density and
to the (vanishing) magnetic current density and ![12ηiklmg [ik],l](article1389x.gif) to the electric
current density.
to the electric
current density.
The paper with Kaufman ended with “Considerations of compatibility and ‘strength’ of the system of
equations”, a section reappearing as the beginning of Appendix II of the 5th Princeton edition. The 16 +
64 variables 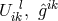 must satisfy the 16 + 64 field equations (311*), (312*). The argument is put forward
that due to
must satisfy the 16 + 64 field equations (311*), (312*). The argument is put forward
that due to 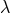 -invariance (identification of connections with different
-invariance (identification of connections with different 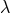 ) the 64
) the 64 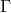 -variables were
reduced to 63 plus an additional identity.
-variables were
reduced to 63 plus an additional identity.
“In a system with no 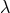 -invariance, there are 64
-invariance, there are 64 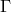 and no counterbalancing identity.
This is the deeper reason for the relative weakness of systems which lack
and no counterbalancing identity.
This is the deeper reason for the relative weakness of systems which lack 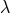 -invariance.
We hold to the principle that the stronger system has to be preferred to any weaker
system, as long as there are no special reasons to the contrary.” ([174*], p. 137.)
-invariance.
We hold to the principle that the stronger system has to be preferred to any weaker
system, as long as there are no special reasons to the contrary.” ([174*], p. 137.)
However, it is to be noted that in the 5th Princeton edition the 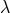 -transformation is reduced to
-transformation is reduced to 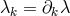 (Eq. (5) on p. 148). In a footnote, Appendix II of the 4th Princeton edition of The Meaning
of Relativity is given as a reference for the concept of “strength” of a system of differential
equations (cf. Section 9.2.3). W. Pauli must have raised some critical questions with regard to
the construction of the paper’s Lagrangian from irreducible quantities. In her answer of 28
February 1956, B. Kaufman defended the joint work with Einstein by discussing an expression
(Eq. (5) on p. 148). In a footnote, Appendix II of the 4th Princeton edition of The Meaning
of Relativity is given as a reference for the concept of “strength” of a system of differential
equations (cf. Section 9.2.3). W. Pauli must have raised some critical questions with regard to
the construction of the paper’s Lagrangian from irreducible quantities. In her answer of 28
February 1956, B. Kaufman defended the joint work with Einstein by discussing an expression
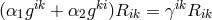 : “Now the point is here that
: “Now the point is here that 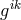 was introduced in our paper merely as a
multiplying function such as to make, together with
was introduced in our paper merely as a
multiplying function such as to make, together with 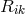 , a scalar. Hence
, a scalar. Hence 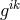 can just as well
be this multiplier. The field equations we would get from this Lagrangian would be identical
with the equations in our paper, except that they would be expressed in terms of
can just as well
be this multiplier. The field equations we would get from this Lagrangian would be identical
with the equations in our paper, except that they would be expressed in terms of 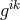 .” As to
scalars quadratic in curvature she wrote: “ […] our paper does not claim that the system we give
is 100% unique. In order to do that one would have to survey all possible additional tensors
which could be used in the Lagrangian. We only considered the most ‘reasonable’ ones.” ([492],
pp. 526–527.)
.” As to
scalars quadratic in curvature she wrote: “ […] our paper does not claim that the system we give
is 100% unique. In order to do that one would have to survey all possible additional tensors
which could be used in the Lagrangian. We only considered the most ‘reasonable’ ones.” ([492],
pp. 526–527.)
Until 1955, more than a dozen people had joined the research on UFT and had published papers.
Nevertheless, apart from a mentioning of H. Weyl’s name (in connection with the derivation of the
“Bianchi”-identities) no other author is referred to in the paper. B. Kaufman was well aware
of this and would try to mend this lacuna in the same year, after Einstein had passed away.
At the “Jubilee Conference” in Bern in July
1955,158
based on her recent work with A. Einstein [174*], B. Kaufman gave an account “[…] of the logical steps
through which one goes when trying to set up this generalization”, i.e., of general relativity to the “theory
of the non-symmetric field” ([322*], p. 227). After she presented essential parts of the joint paper with
Einstein, Kaufman discussed its physical interpretation and some of the consequences of the theory. As in
[148*, 150*], and [156*], the electric current density is taken to be proportional to ![g[ik],l + g[kl],i + g[li],k](article1404x.gif) . From
this identification, transposition invariance receives its physical meaning as showing that “all
equations of the theory shall be invariant under a change of the sign of electric charge” ([322],
p. 229). With (252*), i.e.,
. From
this identification, transposition invariance receives its physical meaning as showing that “all
equations of the theory shall be invariant under a change of the sign of electric charge” ([322],
p. 229). With (252*), i.e., ![ˆg[ik,]k = 0](article1405x.gif) , holding again in the theory,
, holding again in the theory, 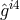 (with
(with  is
identified with the components of the magnetic field. In the linear approximation, the field
equations decompose into the linear approximation of the gravitational field equations of general
relativity and into the weaker form of Maxwell’s equations already shown in (210*), (211*) of
Section 7.3.
is
identified with the components of the magnetic field. In the linear approximation, the field
equations decompose into the linear approximation of the gravitational field equations of general
relativity and into the weaker form of Maxwell’s equations already shown in (210*), (211*) of
Section 7.3.
In the section “Results in the theory” of her paper, Kaufman tried to sum up what was known about the
“theory of the non-symmetric field”. Both in terms of the number of papers published until the beginning of
1955, and of researchers in UFT worldwide, she did poorly. She mentioned Schrödinger, Hlavatý,
Lichnerowicz and M.-A. Tonnelat as well as one or two of their collaborators, and some work done in
Canada and India. The many publications coming from Italian groups were neglected by her as well as
contributions from Japan, the United States and elsewhere which she could have cited. Nevertheless, in
comparison with Einstein’s habit of non-citation, her references constituted a “wealth” of material. Of the
few general results obtained, Lichnerowicz’ treatment of the Cauchy initial value problem for the
weak field equations of UFT and his proof that a unique solution exists seems to be the most
important [369*]. Unfortunately, his proof, within general relativity, that static, regular solutions
behaving asymptotically like a Schwarzschild point particle (with positive mass) are locally
Euclidean, could not be carried over to UFT. This was due to the complications caused by the field
equations (311*), (312*). While (311*) could be solved, in principle, for the 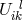 as functions of
as functions of
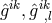 , its subsequent substitution into (312*) led to equations too complicated to be solved
– except in very special cases. In his summary of the conference, Pauli mocked Kaufman’s
report:
, its subsequent substitution into (312*) led to equations too complicated to be solved
– except in very special cases. In his summary of the conference, Pauli mocked Kaufman’s
report:
“We have seen how Einstein and Mrs. Kaufman struggled heroically […], and how this fight
has been led with the particular weapon of the  -transformation. Certainly, all this is
formally very correct; however, I was unable to make sense of the
-transformation. Certainly, all this is
formally very correct; however, I was unable to make sense of the  -transformations,
either physically or geometrically.”[486*]159
-transformations,
either physically or geometrically.”[486*]159
The search for solutions of the weak field equations had begun already with exact spherically
symmetric, static solution derived by a number of authors (cf. [475*, 31*, 32*]; see Sections 8.3, and
9.6).
In a final section, B. Kaufman discussed two alternatives to what she now called “Einstein’s theory” for the first time. The first is Schrödinger’s purely affine version of the theory as presented in his book [557*]. His field equations replacing (289*), (290*) were (cf. Section 8.1, Eq. (237*):
Here, plays the role of cosmological constant. At first, in the affine theory,
plays the role of cosmological constant. At first, in the affine theory, 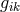 is defined by the
l.h.s. of (315*), but then this equations is read like an Einstein equation for the metric.
is defined by the
l.h.s. of (315*), but then this equations is read like an Einstein equation for the metric.
In a note added for the reprint in 1954 of his book, Schrödinger warned the readers of his chapter on UFT that he did not regard his unification of gravitation and electromagnetism:
“[…] as anything like a well-established theory. It must be confessed that we have as yet no glimpse of how to represent electrodynamic interaction, say Coulomb’s law. This is a serious desideratum. On the other hand we ought not to be disheartened by proofs, offered recently by L. Infeld, M. Ikeda and others, to the effect, that this theory cannot possibly account for the known facts about electrodynamic interaction. Some of these attempts are ingenious, but none of them is really conclusive.” ([557*], reprint 1954, p. 119.)
9.5 Reactions to Einstein–Kaufman
Schrödinger found the paper by Einstein and Kaufman in the Festschrift for L. de Broglie
[172] “very important” and set out to draw some consequences. In particular, by using the
approximation-scheme of Einstein and Kaufman, he showed that “the electric current-four-vector is in
general different from zero throughout the field” ([559*], p. 13). In the strong field equations, ![K [ik] = 0 −](article1417x.gif) led to the vanishing of the electric current density. Dropping the so-called cosmological term
for convenience, Schrödinger now wrote Eq. (316*) of his “weak” field equations in the form:
led to the vanishing of the electric current density. Dropping the so-called cosmological term
for convenience, Schrödinger now wrote Eq. (316*) of his “weak” field equations in the form:
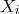 .160
Besides obtaining, in first approximation, Einstein’s vacuum field equations of general relativity and one set
of Maxwell’s equations, he gave as the second set:
From this he concluded that “the curl of the current is essentially the dual of the curl of
.160
Besides obtaining, in first approximation, Einstein’s vacuum field equations of general relativity and one set
of Maxwell’s equations, he gave as the second set:
From this he concluded that “the curl of the current is essentially the dual of the curl of 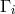 ” (his notation
for
” (his notation
for 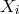 ). Here,
). Here, 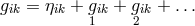 .
.
In 2nd order, the charge-current tensor was defined by ![sijk = g[ij],k + g [jk],i + g[ki],j 2 2 2 2](article1428x.gif) , and the wave
equation then
, and the wave
equation then ![ηrs∂r∂sg [ik] = sijk + ηrm ηsng[rs]B nmik 2 2 1 1](article1429x.gif) .
. 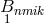 is a linear combination of the 2nd
derivatives of
is a linear combination of the 2nd
derivatives of  . However, Schrödinger rejected this equation: “it is not invariant” ([559*],
p. 19). Since 1952, Cornelius Lanczos had come to Dublin, first as a visiting, then as a senior
professor, and, ultimately, as director at the Dublin Institute for Advanced Studies. In his paper,
Schrödinger acknowledged “discussions with my friend professor Cornel Lanczos” ([559], p.
20).
. However, Schrödinger rejected this equation: “it is not invariant” ([559*],
p. 19). Since 1952, Cornelius Lanczos had come to Dublin, first as a visiting, then as a senior
professor, and, ultimately, as director at the Dublin Institute for Advanced Studies. In his paper,
Schrödinger acknowledged “discussions with my friend professor Cornel Lanczos” ([559], p.
20).
In the Festschrift on the occasion of de Broglie’s 60th anniversary, published only in 1953, C. F. von Weizsäcker expressed his opinion clearly that:
“[…] in the future, no reason exists for connecting the metric more closely to the electromagnetic
field, and perhaps also to the meson field.” ([680], p. 141.)161
One year later, consistent with this, and with Einstein’s death “in April 1955, Schrödinger became quite depressed, for he was now convinced that his unified field theory was no longer tenable” ([446*], p. 326). In any case, there is no further published research on UFT by him.
M. S. Mishra also studied Einstein’s last publication written together with B. Kaufman [174] and solved (311*) for the connection. He obtained M.-A. Tonnelat’s result (364*) of Section 10.2.3 [433]. Instead of beginning with (311*) and (312*) as Einstein and Kaufman had done, he then introduced “another set of field equations” by taking
with the contracted curvature tensor which is transposition-symmetric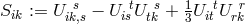 .
The solution to (319*), (320*) is given as:
where
.
The solution to (319*), (320*) is given as:
where 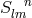 is the torsion tensor, and
is the torsion tensor, and 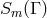 the torsion vector. Mishra then linearized the metric and
showed the result to be equivalent to the linearized Einstein–Straus equations (cf. Section 7.3) In the same
paper, Mishra suggested another set of field equations by starting from the transposed Ricci tensor and
making it transposition invariant in the same manner as Einstein and Kaufman did in their
case.
the torsion vector. Mishra then linearized the metric and
showed the result to be equivalent to the linearized Einstein–Straus equations (cf. Section 7.3) In the same
paper, Mishra suggested another set of field equations by starting from the transposed Ricci tensor and
making it transposition invariant in the same manner as Einstein and Kaufman did in their
case.
In a joint paper with M. L. Abrol, also directed to the Einstein–Kaufman version of Einstein’s theory, Mishra claimed: “It is shown […] that Infeld’s method [cf. [304]] of approximation, to find the equations of motion of charged particles from the system of field equations, fails in this particular theory” [437]. This was due to some unknown terms in the 2nd and 3rd order of the approximation. After a modification of the field equations according to the method of Bonnor [cf. [34*]], the Coulomb force appeared in 4th order.
9.6 More exact solutions
9.6.1 Spherically symmetric solutions
A hope for overcoming the difficulty of relating mathematical objects from UFT to physical observables
was put into the extraction of exact solutions. In simple cases, these might allow a physical
interpretation by which the relevant physical quantities then could be singled out. One most simple case
with high symmetry is the static spherically symmetric (sss) field. Papapetrou’s solution of
Section 8.3 soon was generalized to the case 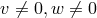 by Wyman [709*] which means
that both, electric and magnetic fields, are now present. Wyman’s three different solutions
of the weak field equations contain one arbitrary function of the radial coordinate
by Wyman [709*] which means
that both, electric and magnetic fields, are now present. Wyman’s three different solutions
of the weak field equations contain one arbitrary function of the radial coordinate  , each.
Wyman questioned the physical interpretation of
, each.
Wyman questioned the physical interpretation of 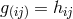 and
and ![g[ij] = kij](article1440x.gif) as standing for
the gravitational field and the electromagnetic field, respectively. He built another expression:
as standing for
the gravitational field and the electromagnetic field, respectively. He built another expression:
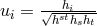 and
and 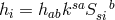 . If
. If  is chosen as a metric, then the unique solution of general
relativity in this sss case, e.i., the Schwarzschild solution, results. Although Wyman’s construction was very
artificial, it clearly exemplified the unsurmountable impediment to UFT: the “embarras de richesses” in
mathematical objects.
is chosen as a metric, then the unique solution of general
relativity in this sss case, e.i., the Schwarzschild solution, results. Although Wyman’s construction was very
artificial, it clearly exemplified the unsurmountable impediment to UFT: the “embarras de richesses” in
mathematical objects.
Wyman also questioned the boundary condition used at spacelike infinity: 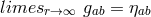 , where
, where
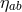 is the Minkowski metric. By looking at his (or Papapetrou’s) sss solutions, he showed that different
boundary condition could be set up leading to different solutions:
is the Minkowski metric. By looking at his (or Papapetrou’s) sss solutions, he showed that different
boundary condition could be set up leading to different solutions:  for
for  or
or  for
for
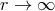 .
.
Apparently, this left no great impression; the search for sss solutions continued. As two sets of field
equations were competing against each other, Einstein’s (and Schrödinger’s) weak and strong equations
(with or without cosmological constant 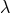 ), we must distinguish the solutions suggested. In the case of
sss fields, only one additional field equation, e.g.,
), we must distinguish the solutions suggested. In the case of
sss fields, only one additional field equation, e.g., ![R [23] = 0](article1452x.gif) , separates the strong from the
weak equations. For the strong equations with
, separates the strong from the
weak equations. For the strong equations with 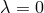 , Bonnor [31] obtained the general exact
solution in the cases for which either a magnetic or an electric field is present. He also generalized
Papapetrou’s solution for the weak equations to the case where the function
, Bonnor [31] obtained the general exact
solution in the cases for which either a magnetic or an electric field is present. He also generalized
Papapetrou’s solution for the weak equations to the case where the function  is real or imaginary.
The solutions describe spread out charges while the masses are banned into singularities. All
solutions display an infinite set of “singular” surfaces between the radial coordinate
is real or imaginary.
The solutions describe spread out charges while the masses are banned into singularities. All
solutions display an infinite set of “singular” surfaces between the radial coordinate 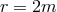 and
and
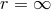 .162
For some time, after a note by Bandyopadhyay [8], who claimed that for the
strong equations
.162
For some time, after a note by Bandyopadhyay [8], who claimed that for the
strong equations 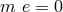 where
where 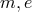 are the parameters for mass and
charge,163
a discussion took place whether isolated massless magnetic monopoles could exist. Since 1948, Papapetrou
and Schrödinger had changed the assignment of components of
are the parameters for mass and
charge,163
a discussion took place whether isolated massless magnetic monopoles could exist. Since 1948, Papapetrou
and Schrödinger had changed the assignment of components of 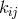 to the electric and magnetic fields;
now
to the electric and magnetic fields;
now ![g ,g ,g [23] [31] [12]](article1464x.gif) stood for the electric field [479]. Ikeda, in a paper of 1955, claimed to have shown “that
a single magnetic pole cannot exist in the Einstein new theory, as in the Maxwell theory” ([298*],
p. 272).164
This result depended on Ikeda’s identification of the electromagnetic field with
stood for the electric field [479]. Ikeda, in a paper of 1955, claimed to have shown “that
a single magnetic pole cannot exist in the Einstein new theory, as in the Maxwell theory” ([298*],
p. 272).164
This result depended on Ikeda’s identification of the electromagnetic field with
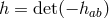 . In 1960, Bandyopadhyay came back to the question and claimed that “the
‘stronger’ equations will not allow isolated magnetic poles with mass whereas the ‘weaker’ equations will
allow the existence of such entities” ([10], p. 427). Bonnor’s second paper of 1952 dealt with the strong
equations in the case
. In 1960, Bandyopadhyay came back to the question and claimed that “the
‘stronger’ equations will not allow isolated magnetic poles with mass whereas the ‘weaker’ equations will
allow the existence of such entities” ([10], p. 427). Bonnor’s second paper of 1952 dealt with the strong
equations in the case 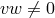 . Again, the exact solutions described spread out charges of both signs with
an infinity of singular surfaces. They were unphysical because they contained no parameter for the mass of
the sources [32*].
. Again, the exact solutions described spread out charges of both signs with
an infinity of singular surfaces. They were unphysical because they contained no parameter for the mass of
the sources [32*].
In her book, M.-A. Tonnelat discussed these solutions; her new contribution consisted in the calculation
of the components of her connection  – Schrödinger’s star connection (27*) - and the Ricci
– Schrödinger’s star connection (27*) - and the Ricci
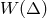 -tensor formed from it for the more general case of time-dependent spherically symmetric fields
[629], ([632*], p. 71, 73). By help of this calculation, her collaborator Stamatia Mavridès could present a
general result: for
-tensor formed from it for the more general case of time-dependent spherically symmetric fields
[629], ([632*], p. 71, 73). By help of this calculation, her collaborator Stamatia Mavridès could present a
general result: for ![g[23] = 0,g[10] ⁄= 0](article1470x.gif) (as the non-vanishing components of
(as the non-vanishing components of 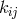 ) only static exact
spherically symmetric solutions do exist [402]. Later in Italy, F. De Simoni published another generalization
of Wyman’s and Bonnor’s solutions for the weak field equations; he used the Ricci tensor of Einstein and
Straus (73*) made Hermitian, i.e.,
) only static exact
spherically symmetric solutions do exist [402]. Later in Italy, F. De Simoni published another generalization
of Wyman’s and Bonnor’s solutions for the weak field equations; he used the Ricci tensor of Einstein and
Straus (73*) made Hermitian, i.e., 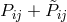 . His paper is not referred to in Tonnelat’s book [114].
J. R. Vanstone mistakenly believed he had found time-dependent spherically symmetric solutions,
but the time dependency can be easily removed by a coordinate transformation [668]. Also
B. R. Rao had calculated some, but not all components of the connection for the case of a
time-dependent spherically symmetric field but had failed to find a time-dependent solution
[502].
. His paper is not referred to in Tonnelat’s book [114].
J. R. Vanstone mistakenly believed he had found time-dependent spherically symmetric solutions,
but the time dependency can be easily removed by a coordinate transformation [668]. Also
B. R. Rao had calculated some, but not all components of the connection for the case of a
time-dependent spherically symmetric field but had failed to find a time-dependent solution
[502].
Unfortunately, all this work did not bring further insight into the physical nature of the sss solutions.
The only physically “usable” solution remained Papapetrou’s. He also proved the following theorem:
“Spherically-symmetric solutions periodical in time of the “weak” field equations satisfying the boundary
conditions 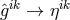 for
for 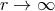 are, in 1st approximation, identical to solutions of the “strong”field
equations” [478].
are, in 1st approximation, identical to solutions of the “strong”field
equations” [478].
9.6.2 Other solutions
Still worse, in 1958 a sobering contribution from the Canadian mathematician Max Wyman and his German colleague Hans Zassenhaus cast doubt on any hope for a better understanding of the physical contents of UFT by a study of exact solutions. They investigated solutions of Einstein’s non-symmetrical UFT with vanishing curvature tensor: in this case weak and strong field equations coincide. Unlike for flat space-time in general relativity, a large class of solutions resulted; a situation which, according to the authors, “[…] merely adds to the confusion and indicates that the form of the theory is far from complete”. They went on: “However, as far as a satisfactory physical interpretation of such a theory goes, almost complete chaos seems to result.” ([710*], p. 228.) Strong words, indeed, but not without reason:
“[…] for a theory based on a non-symmetric tensor an infinity of tensors of all orders exist. The only hope to extract from this maze the proper mathematical expressions to use for physical quantities would thus have to be physical in nature. So far no such physical assumptions have been put forward” ([710], p. 229).
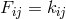 electromagnetic field,
electromagnetic field, 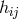 gravitational potential) “would
attribute the electromagnetic field to a distribution of charge along the infinite planes
gravitational potential) “would
attribute the electromagnetic field to a distribution of charge along the infinite planes  or along
any of the equipotential
or along
any of the equipotential  .” For a weak gravitational field, the Newtonian
potential would be
.” For a weak gravitational field, the Newtonian
potential would be 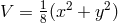 “corresponding to a distribution of mass of density
“corresponding to a distribution of mass of density 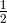 inside an infinite cylinder”. This is due to the approximated Newtonian equations of motion
following from the geodesic equation for
inside an infinite cylinder”. This is due to the approximated Newtonian equations of motion
following from the geodesic equation for 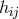 . Hence, for this solution, mass and charge are
unrelated.
. Hence, for this solution, mass and charge are
unrelated.
This result casts into doubt much of the work on exact solutions independently of any specific assignment of mathematical objects to physical variables. It vindicated Schrödinger’s opinion that exact solutions were of useless for a better understanding of the particle-aspect of the theory; cf. the quotation at the end of Section 8.2. Nevertheless, the work of assembling a treasure of exact solutions continued. In 1954, it had still been supported by Kilmister & Stephenson in this way: ‘The true test of this theory [i.e., Einstein’s weak field equations] as an adequate description of the physical world must await exact solutions of the field equations” [331].
Einstein did not live to see the results of Wyman & Zassenhaus; now some of the non-singular exact solutions of the field equations of UFT he so much wished to have had, were at hand:
“The big difficulty [of UFT] lies in the lack of a method for deriving singularity-free exact
solutions which alone are physically interesting. Yet the bit we have been able to calculate
has strengthened my trust in this theory.” (Einstein to Pauli, April 1, 1948 quoted from
[489*])165
How would he have dealt with the fact, unearthed in 1958, that such non-singular solutions not always offered a convincing physical interpretation, or even were unphysical?
The symmetry of so-called “1-dimensional” gravitational fields of general relativity, i.e., those for which
the metric components depend on only a single coordinate, is high enough to try and solve for them field
equations of UFT. In fact, already in 1951, Bandyopadhyay had found such a solution of the weak equations
with ![g ⁄= 0, g = 0,g = g [10] [23] 22 33](article1483x.gif) and had taken it as describing an infinite charged plate [7*]. In 1953,
E. Clauser presented another such 1-dimensional field as a solution of the weak equations with
and had taken it as describing an infinite charged plate [7*]. In 1953,
E. Clauser presented another such 1-dimensional field as a solution of the weak equations with 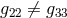 and saw it as representing a magnetostatic field [79]. B. R. Rao in 1959 generalized Bandyopadhyay’s
solution to the case
and saw it as representing a magnetostatic field [79]. B. R. Rao in 1959 generalized Bandyopadhyay’s
solution to the case ![g[10] × g[23] ⁄= 0](article1485x.gif) without attempting to provide a physical interpretation
[503].
without attempting to provide a physical interpretation
[503].
Plane wave solutions of the weak and strong field equations of the form
with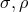 functions of
functions of 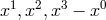 have been given by Takeno [601].
have been given by Takeno [601].
9.7 Interpretative problems
Already up to here, diverse assignments of geometrical objects to physical quantities (observables) were
encountered. We now assemble the most common selections.
a) Gravitational Field
From the fact that the exact, statical, spherically symmetric solution of the weak field equations derived
by A. Papapetrou did not coincide asymptotically, or far from the assumed location of the point source at
 , i.e., for
, i.e., for  , with the corresponding solution of the Einstein–Maxwell equations
(Reissner–Nordström) [475*], a discussion of the relation between geometrical objects and physical
observables arose. Perhaps the metric chosen to describe the gravitational potential ought not to be
identified with
, with the corresponding solution of the Einstein–Maxwell equations
(Reissner–Nordström) [475*], a discussion of the relation between geometrical objects and physical
observables arose. Perhaps the metric chosen to describe the gravitational potential ought not to be
identified with 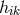 ! Let the inverse of
! Let the inverse of 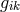 be given by
be given by
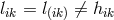 of
of 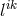 as the genuine metric ([371*], p. 288). Schrödinger had already worked with it. A
related suggestion made by several doctoral students of M.-A. Tonnelat (J. Hély, Pham Tan Hoang,
M. Lenoir) was to use
as the genuine metric ([371*], p. 288). Schrödinger had already worked with it. A
related suggestion made by several doctoral students of M.-A. Tonnelat (J. Hély, Pham Tan Hoang,
M. Lenoir) was to use 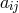 with
with 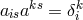 and
and 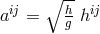 as metric [250, 271*, 272*], ([359*], p. 92).
In Section 9.6.1 we have seen that by another, if only very contrived definition of the metric, complete
separation of the gravitational and electromagnetic fields could be achieved: the Schwarzschild solution
could be made part of an exact solution of unified field theory [709]. The torsion tensor appeared in the
definition of this metric.
as metric [250, 271*, 272*], ([359*], p. 92).
In Section 9.6.1 we have seen that by another, if only very contrived definition of the metric, complete
separation of the gravitational and electromagnetic fields could be achieved: the Schwarzschild solution
could be made part of an exact solution of unified field theory [709]. The torsion tensor appeared in the
definition of this metric.
b) Electromagnetic Field and Charge Currents
The same ambiguity arose for the description of the electromagnetic field: Einstein’s specification that it
be connected to ![kij = g[ij]](article1499x.gif) was taken over by the majority ([147*], p. 583). For dimensional
reasons, this interpretation implies that a constant of dimension “length” will appear in the
theory. In her discussion of two possibilities, St. Mavridès suggested
was taken over by the majority ([147*], p. 583). For dimensional
reasons, this interpretation implies that a constant of dimension “length” will appear in the
theory. In her discussion of two possibilities, St. Mavridès suggested 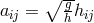 for the
metric and
for the
metric and 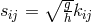 for the electromagnetic field [403, 400*, 401*, 404]. The first choice was
supported by Pham Tan Hoang [271*, 272*]. Although making the electrical field regular at
for the electromagnetic field [403, 400*, 401*, 404]. The first choice was
supported by Pham Tan Hoang [271*, 272*]. Although making the electrical field regular at 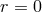 :
:
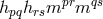 and
and 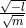 with
with 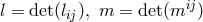 ([641*], p. 345); cf. Section 5.
Mme. Tonnelat, in her books, also discussed in detail how to relate observables as the gravitational and
electromagnetic fields, the electric current density, or the energy-momentum tensor of matter
to the geometric objects available in the theory ([632*], Chapter VI; [636*, 382*]; cf. also
Section 10.2.1). For the electromagnetic field tensor, four possibilities were claimed by her to be
preferable:167
([641*], p. 345); cf. Section 5.
Mme. Tonnelat, in her books, also discussed in detail how to relate observables as the gravitational and
electromagnetic fields, the electric current density, or the energy-momentum tensor of matter
to the geometric objects available in the theory ([632*], Chapter VI; [636*, 382*]; cf. also
Section 10.2.1). For the electromagnetic field tensor, four possibilities were claimed by her to be
preferable:167
![mik; mik;K [ik];𝜖ijklmkl](article1517x.gif) . Tonnelat opted for
. Tonnelat opted for 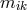 , and also for the electric current density vector
, and also for the electric current density vector
![J i = √1--𝜖ijkl(m + m + m ) 6 −h [ij],k [ki],j [jk],i](article1519x.gif) . The field induction is defined via:
. The field induction is defined via: 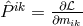 . Schrödinger had
identified the electromagnetic field with the anti-symmetrical part
. Schrödinger had
identified the electromagnetic field with the anti-symmetrical part ![K [ik]](article1521x.gif) of the Ricci tensor [545*, 549*]; this
suggestion was also made in [138*, 141, 5*, 93*]. On the other hand, Eq. (235*) can be satisfied by
of the Ricci tensor [545*, 549*]; this
suggestion was also made in [138*, 141, 5*, 93*]. On the other hand, Eq. (235*) can be satisfied by
![ˆg[ij] = 12𝜖ijkl(∂kAl − ∂lAk)](article1522x.gif) such that
such that ![Fij := 𝜖ijklˆg[kl] = ∂iAj − ∂jAi](article1523x.gif) would naturally constitute the
relationship to the electromagnetic field tensor
would naturally constitute the
relationship to the electromagnetic field tensor 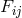 [203*]. In this context, the electromagnetic induction
would be
[203*]. In this context, the electromagnetic induction
would be 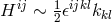 , and alternatively,
, and alternatively, 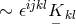 ([650*], p. 370). We learned above in
(323*) of Section 9.6.1 that M. Ikeda used yet another definition of the electromagnetic field
tensor.
([650*], p. 370). We learned above in
(323*) of Section 9.6.1 that M. Ikeda used yet another definition of the electromagnetic field
tensor.
If electrical currents are to be included, the following choices for the current density were considered by Einstein, by Straus, (cf. Sections 9.2.2 and 9.3), and by others [34*, 637*]:
The second choice would either violate the weak field equations or forbid any non-zero current density. These alternatives are bound to the choice for the induction. Two possibilities were discussed by Mavridès: In the 2nd case, Papapetrou’s spherically symmetric static solutions would not make sense, physically [407].168 Finzi proposed yet another expression: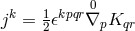 ([473*], p. 288). Late in his life, Einstein gave
([473*], p. 288). Late in his life, Einstein gave
![[is] ˆg ,s](article1531x.gif) the interpretation of magnetic current density [158*].
the interpretation of magnetic current density [158*].
An ambiguity always present is the assignment of the electric and magnetic fields to the
components 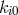 or
or 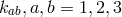 , or vice versa in order to arrive at the correct Maxwell’s
equations.
, or vice versa in order to arrive at the correct Maxwell’s
equations.
Another object lending itself to identification with the electromagnetic field would be homothetic
curvature encountered in Section 2.3.1, i.e., 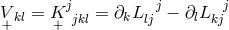 :
: 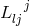 could then play the role
of the vector potential. This choice has been made by Sciama, but with a complex curvature tensor
could then play the role
of the vector potential. This choice has been made by Sciama, but with a complex curvature tensor 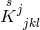 [565*]. In this case
[565*]. In this case ![sj j j K jkl = ∂kL [lj] − ∂lL[kj] = 2S[j,k]](article1537x.gif) . The vector potential thus is identified with the torsion
vector.
. The vector potential thus is identified with the torsion
vector.
In a paper falling outside of the period of this review, H.-J. Treder suggested to also geometrize spinorial degrees of freedom by including them in the asymmetric metric; it took the form [651, 67]:
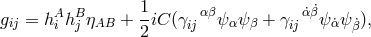
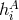 are tetrad components,
are tetrad components, 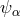 a 2-component Weyl-spinor,
a 2-component Weyl-spinor, 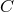 a constant (with dimension) and
a constant (with dimension) and
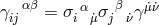 .
. 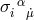 are Pauli-matrices,
are Pauli-matrices, 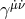 corresponds to the antisymmetric
corresponds to the antisymmetric  symbol
symbol
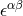 .
It is obvious that the assumed mapping of geometrical objects to physical variables had to remain highly
ambiguous because the only arguments available were the consistency of the interpretation within unified
field theory and the limit to the previous theories (Einstein–Maxwell theory, general relativity), thought to
be necessarily encased in UFT. As we have seen, the hope of an eventual help from exact solutions had to
be abandoned.
.
It is obvious that the assumed mapping of geometrical objects to physical variables had to remain highly
ambiguous because the only arguments available were the consistency of the interpretation within unified
field theory and the limit to the previous theories (Einstein–Maxwell theory, general relativity), thought to
be necessarily encased in UFT. As we have seen, the hope of an eventual help from exact solutions had to
be abandoned.
c) Matter tensor
In Einstein’s understanding of UFT, the matter tensor for a continuous matter distribution should also become part of geometry. Again a precise attribution to geometrical objects could not be found. One way of approaching the problem was to reshape part of the field equations into the form of the old or a newly defined “Einstein tensor”, and terms left over. These then were declared to constitute the “matter tensor”. In her book, M.-A. Tonnelat discussed this problem in detail ([632*], Chapter VII, A, pp. 109–117); cf. also Section 10.3.1. As late as 1963, Schrödinger could write:
“Thus it is as yet undecided what interpretation of the various tensors and densities is most likely to let the theory meet observed facts” ([557], reprinted 1963, p. 115).
9.8 The role of additional symmetries
The symmetries Einstein had introduced, i.e., transposition invariance and  -transformations, played a
major role in versions of UFT, but not in physics, in general. There are only a few papers with these
symmetries as their topic. J. Winogradzki investigated the relationship of the results in Einstein’s
final approach to UFT (made together with B. Kaufman) to the theorems by Emmy Noether
[704*, 703*]. She called invariance with regard to the group
-transformations, played a
major role in versions of UFT, but not in physics, in general. There are only a few papers with these
symmetries as their topic. J. Winogradzki investigated the relationship of the results in Einstein’s
final approach to UFT (made together with B. Kaufman) to the theorems by Emmy Noether
[704*, 703*]. She called invariance with regard to the group  composed of coordinate- and
composed of coordinate- and
 -transformations which had been named the “extended” group by Einstein,
-transformations which had been named the “extended” group by Einstein, 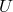 - or
- or 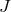 - invariance:
- invariance:
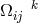 being independent of
being independent of 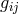 . As a necessary condition for the field equations following from a
variational principle to be J-invariant, she derived
. As a necessary condition for the field equations following from a
variational principle to be J-invariant, she derived 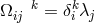 . Thus, with the help of four axioms
postulated by her, she arrived at the
. Thus, with the help of four axioms
postulated by her, she arrived at the  -transformations (52*).
-transformations (52*).
According to the 2nd theorem by E. Noether,  -invariance leads to four identities which were written
out by Winogradzki for a Lagrangian density
-invariance leads to four identities which were written
out by Winogradzki for a Lagrangian density  (her “Hamiltonian”):
(her “Hamiltonian”):
![[is] ˆg ,s = 0](article1560x.gif) and the 16 field equations which are not invariant under
and the 16 field equations which are not invariant under
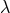 -transformations.
-transformations.
P. G. Bergmann also discussed Einstein’s 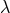 -transformations, but just in the special form used in the
5th edition of The Meaning of Relativity, i.e., with
-transformations, but just in the special form used in the
5th edition of The Meaning of Relativity, i.e., with 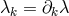 . No wonder that he then concluded: “[…] the
. No wonder that he then concluded: “[…] the
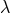 transformation appears to be closely related in its conception to Weyl’s original gauge transformation”
([23], p. 780).
transformation appears to be closely related in its conception to Weyl’s original gauge transformation”
([23], p. 780).


![i+k− ˆg ||l = 0, (249 ) P(ik) = 0, (250 ) P[ik],l + P [kl],i + P[li],k = 0. (251 )](article1153x.gif)
![[ik] s gˆ ,k = 0, Γ [ks] = 0. (252 )](article1154x.gif)



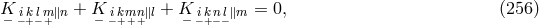
![gkl[− K + K + Σ ] = 0. (257 ) k+l−∥m k+m+ ∥l −lm− ∥k](article1180x.gif)
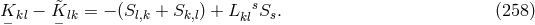
![gkl[− K + K + K ] = 0. (259 ) k+l−∥m k+m+∥l m− l−∥k](article1192x.gif)
![kl g [− K [kl]∥m + K[km]∥l + K [m l]∥k] = 0. (260 ) +− ++ − −](article1194x.gif)
![gkl[− K + K + K − K + K + K ] = 0. (261 ) (k+l−)∥m (+km+)∥l (m− l)−∥k [k+l]−∥m [k+m+]∥l [m− l−]∥k](article1195x.gif)
![gkl[− K + K + K ] = 0. (262 ) (k+l−)∥m (k+m+)∥l (−ml−)∥k](article1196x.gif)
![gkl[K [kl],m + K [mk],l + K [lm],k] = 0, (263 ) − − −](article1197x.gif)
![K− [kl],m + K− [lm],k + K− [mk ],l = 0 (264 )](article1198x.gif)

![g ik∥l := gik,l − grkLilr− girLlkr= 0, (266 ) +− m Sj (L ) := L [im] = 0, (267 ) Kjk (L) = 0. (268 )](article1206x.gif)
![[il] ˆg , l = 0 (269 )](article1210x.gif)
![[il] ˆg+− = ˆg[il] − ˆg[il]Sl. (270 ) ||l ,l](article1211x.gif)

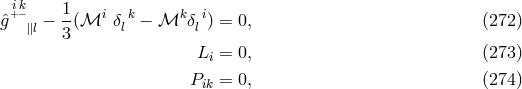
![ℳi ≡ ˆg[il],l − gˆ[il] Γ l (276 )](article1229x.gif)
![ik ˆg+− ||l = 0, Li = 0, P(ik) = 0, (277 ) P[ik],l + P [kl],i + P[li],k = 0. (278 )](article1233x.gif)

![( ) [ ( ) ( ′) ] z = p n + 3 − s n + 3 − q − w n + 3 − q (280 ) n n − q n − q′ ( ) { z z } = n + 3 a + -1 + -2-+ ... , (281 ) n n n2](article1263x.gif)



![ˆV ikl = 0, ˆg[il], l = 0, Wik + σ [i,k] = 0. (285 )](article1296x.gif)
![ik [il] ˆV l = 0, ˆg , l = 0, W (ik) = 0, W [ik],l + W [kl],i + W [li],k = 0. (286 )](article1298x.gif)
![ˆg = 0, (287 ) i+k−||l Γ i = 0, (288 ) K− (ik) = 0, (289 ) K− [ik],l + K− [kl],i + K− [li],k = 0, (290 )](article1300x.gif)
![∗Γ l:= Γ l+ 2δ lΓ k] (291 ) ik ik 3 [i](article1303x.gif)
![ˆg[il] = 0. (292 ) ,l](article1307x.gif)
![g = 0, (293 ) ik ||∗l K = 0, (294 ) ∗ (ik) K [ik],l + K [kl],i + K [li],k = 0. (295 ) ∗ ∗ ∗](article1308x.gif)
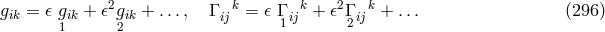


![kl g [− gk+−l∥m + gk+m+∥l + gm− l−∥k] = 0. (299 )](article1340x.gif)
![ˆg [il],l = 0, (300 ) 2 K− (ik) + p (hij − bij) = 0, (301 ) 2 K− [ik],l + K− [kl],i + K− [li],k + p (k[ik],l + k[kl],i + k [li],k) = 0, (302 )](article1341x.gif)


![∗ K− (Γ )ik = K− (Γ )ik − 2Λ [i,k], (305 )](article1363x.gif)
![∗ rs ℋ (Γ ) = ℋ (Γ ) − 2ˆg Λ[r,s]. (306 )](article1364x.gif)

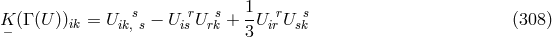
![′ l l l Uik = Uik + 2δ[iλk ]. (309 )](article1377x.gif)
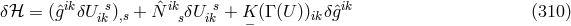
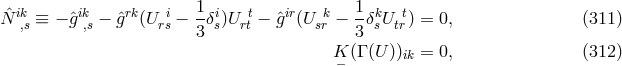


![K = λ g , (315 ) − (ik) ik K [ik],l + K [kl],i + K [li],k = λ(g[ik],l + g[kl],i + g[li],k). (316 ) − − −](article1414x.gif)
![K + X = 0 (317 ) − [ik] [i,k]](article1418x.gif)
![ηrs∂r∂sg[ik] − 2X [i,k] = 0. (318 ) 1](article1424x.gif)
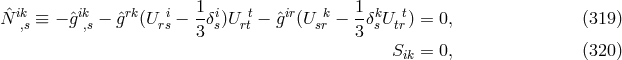
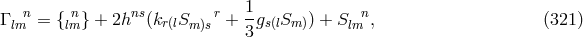
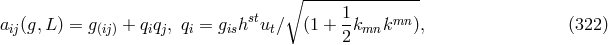
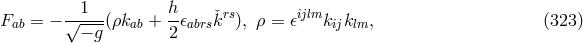
![2 i j 1- 2 2 2 2 2 2 1- 1- ds = hijdx dx = [1 + 4(x + y )]dt − dx − dy − dz , F10 = − 2 x, F20 = − 2 y, (324 )](article1475x.gif)
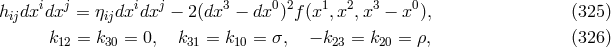
![gik = l(ik) + m [ik]. (327 )](article1493x.gif)

![jijk := g{[ij],k}, (329 ) jijk := K {[ij],k}. (330 ) −](article1527x.gif)
![jijk := k{[ij],k}, (331 ) 1 √ ---- 4 πji := √----∂l( − hhirhlskrs). (332 ) − h](article1528x.gif)
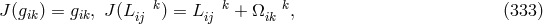
![l-δAˆ- [ms] δkδΓ l − 2ˆg ,s = 0. (334 ) km](article1559x.gif)